4.4 Объединенное решение

В работе [1] приведены аналитические решения для расчета относительных термических напряжений в любой точке неограниченной пластины при ее конвективном нагреве в печи с постоянной температурой греющей среды .

Целью данного раздела является создание объединенного уравнения для аналитического определения указанных величин для тел простой геометрической формы.

Поэтому задачу определения термических напряжений в телах простой формы будем решать в предположении такой же их зависимости от температур на поверхности, в центре и среднемассовой как для плоских тел.

Для цилиндрических тел согласно [8] будут справедливы уравнения (1)...(7), (9), (10) для пластины с заменой координатной функции , входящей в уравнение (4) , где .

Следует отметить, что простому объединению «поддаются» не все величины. Так, амплитуды и легко обобщаются формулами

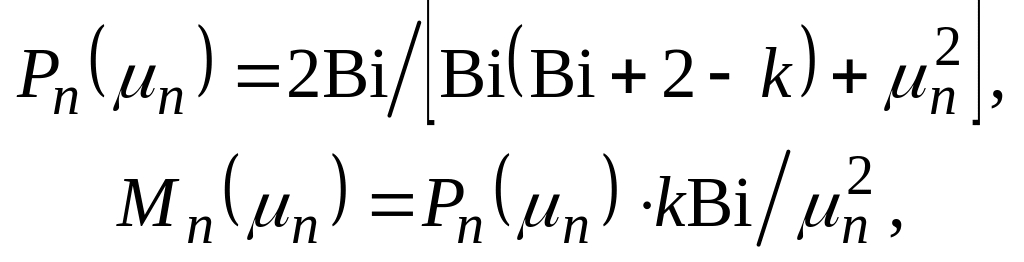(4.159)

а для амплитуды

, (4.160)

где ;

— коэффициент геометрической формы, равный 1 — для пластины, 2 — цилиндра и 3 — шара; ; .

Дифференцируя уравнения (2), (3) и (6) по времени, приравнивая производную нулю и используя два члена суммы ряда, получим формулы для расчёта максимальных времен Фурье:

, (4.161)

где ; ; ; ; .

Подставляя из (18) в уравнения (2), (6) и (3), получим максимальные значения величин с учётом двух членов ряда:

(4.162)

При , имеем время и максимальное термическое напряжение на поверхности ; при , и и при , и .

Анализ полученных решений.

В работе [3] приведена общая приближенная формула расчета первого корня для тел простой формы

, (4.163)

где ; — коэффициент термической массивности; ; ;  — см. уравнение (4.160); при малых  число .

Для определения приближенных значений остальных корней следует различать два характерных случая нагрева при больших и малых числах Био [4, 5, 6].

При малых числах Био (Bi < 3)

, (4.164)

где — корни уравнений (8), (14), (15) при .

При больших числах Био ( )

, (4.165)

где ; — корни уравнений (8), (14), (15), при .

Следует отметить, что при числах Био первый корень следует вычислять не по уравнению (4.163), а по (4.165).

Получим упрощенные расчетные соотношения в двух предельных случаях.

Асимптотика при малых числах Био. Первый корень характеристического уравнения вычисляем по соотношению (4.163), а второй — по (4.164). Тогда отношение собственных чисел

. (4.166)

Разность квадратов корней .

Первая амплитуда, входящая в характеристическое уравнение температуры поверхности

. (4.167)

По аналогии любая амплитуда

, (4.168)

где — n-ый коэффициент термической массивности; .

Интересно отметить, что в отличие от других амплитуд зависимость от числа Био носит немонотонный характер, возрастает от нуля до максимального значения при числе , а затем уменьшается до нуля, оставаясь меньше .

Введем отношение поверхностных амплитуд

, (4.169)

где .

При определении тепловой амплитуды воспользуемся разложением функций уравнения (4.160) при малых аргументах и обобщая эти разложения, получим

, (4.170)

где .

Для среднемассовой температуры:

и

. (4.171)

Для перепада температур по характеристическому уравнению

. (4.172)

Для термических напряжений в центре тела

. (4.173)

Для термонапряжений на поверхности

,

. (4.174)

С целью проверки амплитуды можно использовать равенство .

Выражения для расчета максимальных времен по уравнению (4.161) также упростятся.

Коэффициент поверхности

,

для перепада температур

(4.175)

и центра

Для оценки различия наиболее возможных максимальных времен, которые получаются в предельном случае при числах , с помощью уравнений (4.174) составим их разности

(4.176)

(4.177)

Результаты расчетов разности чисел Фурье по уравнениям (4.175) и (4.176) при и различном коэффициенте геометрической формы приведены в табл. 1.

Таблица 4.3. Разности максимальных времен в зависимости от при

Фактор формы
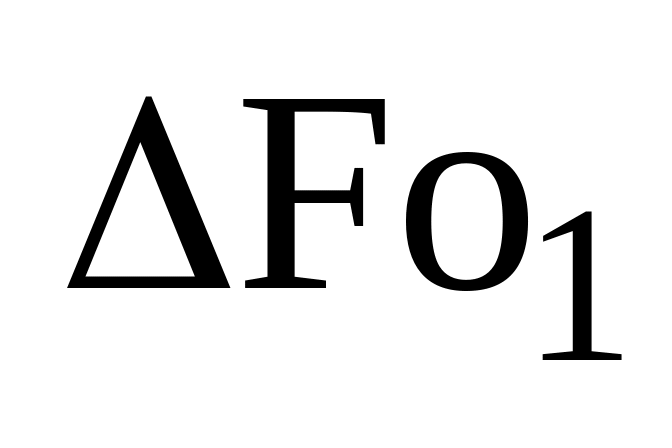
1		0,5703	0,1846	0,7548
2	3,83172	0,2040	0,0872	0,2912
3		0,1166	0,0725	0,1891

Из анализа данных табл. 1 следует, что с ростом коэффициента , т. е. при переходе от плоских тел к сферическим, разности уменьшаются примерно в 3—1,5 раза. Во столько же раз больше чем .

Для выяснения динамики изменения термических напряжений от фактора формы и других числах Био поступим следующим образом.

Результаты расчетов при максимальных времен по формуле (4.161) и соответствующих этим временам максимальных термических напряжений на поверхности и термонапряжений в центре цилиндра по уравнению (4.162) приведены в табл. 4.4. Там же представлены данные при .

Таблица 4.4. Коэффициенты , максимальные времена , , и при и

Пластина
j	Число Био
1	0,121350	0,191828	0,208348		1	0	1
2	0,082567	0,226851	–0,308331		1/3	0,05666	–0,98655
3	0,051086	0,270518	–0,101940		0,09993	0,11669	–0,30838
Цилиндр
1	0,197757	0,107580	0,159022		1	0	1
2	0,101231	0,152028	–0,306990		0,28556	0,05074	–0,96792
3	0,069533	0,176960	–0,152620		0,14446	0,07833	–0,46734
Шар
1	0,249570	0,070318	0,13075	1		0	1
2	0,099923	0,116690	–0,30837	1/4		0,04682	–0,9449
3	0,073222	0,132440	–0,18445	0,16172		0,06153	–0,5688

Анализ уравнений (4.161) и табл. 4.4 позволяет сделать вывод о том, что максимум величин наступает в последовательности и с ростом числа Био эти времена уменьшаются, а различия максимальных времен увеличиваются, вплоть до — см. табл. 4.4 для цилиндра.

На практике технологов интересует вопрос — насколько термические напряжения на поверхности тела больше, чем в его середине. Обозначим их отношение . Наиболее просто можно найти в стадии регулярного режима нагрева (РРН), который наступает при числах Фурье и когда вместо бесконечных сумм в характеристических уравнениях можно ограничиться одним членом ряда. Тогда, деля эти уравнения и учитывая упрощенные соотношения (4.173) и (4.174), получим

(4.178)

При числе .

Таким образом, в отличие от процесса нагрева плоских тел, когда при , термические напряжения на поверхности тела в 2 раза больше термонапряжений в центре, при нагреве цилиндрических тел напряжения в центральных точках тела примерно равны или чуть больше, чем на поверхности.

Отношение термонапряжений при .

Следует отметить, что если приближенно считать , то из характеристического уравнения будем иметь

, (4.179)

где .

Это соотношение при и 2 полностью совпадает с формулами Н.Ю. Тайца [2] для максимальных термических напряжений

. (4.180)