4.3.2. Расчет при больших числах Био

Теперь корни находим по уравнению (4.122). Тогда отношение

(4.138)

где ; ; ; ; ; ; .

В предельном случае, при отношение .

Разность квадратов корней

(4.139)

Амплитуды:

; ,

где ; .

;

,

где и — амплитуды при .

; ,где

; .

; ; ;

.

; ; ; .

_{; ; ; .}

Теперь коэффициенты для расчета максимальных времен примут вид:

; (4.140)

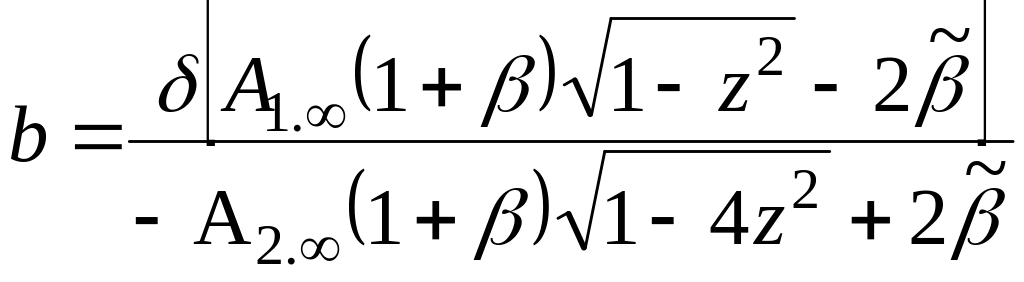(4.141)

; (4.142)

В предельном случае при :

; ;

(4.143)

Так как лишено физического смысла, следует взять .

Тогда наименьшие максимальные времена согласно (4.115) при будут:

,

и . (4.144)

Подставляя (4.144) в уравнение (4.120), получим максимально возможное термическое напряжение в центре шара

. (4.145)

Величины , вычисленные по уравнению (4.143), времена согласно (4.144) и максимальные термические напряжения приведены в табл. 4.2.

Термонапряжение на поверхности при времени

и отношение напряжений в этот момент времени

.

Последняя несколько больше, чем отношение , которое получено для стадии РРН с учетом одного первого члена ряда.

Следует отметить, что если приближенно считать , то из уравнения (4.126) будем иметь

, (4.146)

где .

Это соотношение при и 2 полностью совпадает с формулами Н.Ю. Тайца [7] для максимальных термических напряжений

, (4.147)

где t = t_n - t_ц().

Из анализа уравнения (4.140) вытекает, что коэффициент меняет знак по причине изменения знака амплитуды , изменяющейся от при малых числах Био до . Из условия равенства нулю можно получить граничное число выше которого имеем случаи нагрева термически «массивного» тела. Таким образом, при числах для определения времени можно применять формулу (4.139) в которой определяется по уравнению (4.140), а при коэффициент становится отрицательным и нельзя пользоваться формулой (4.13). Возникшую ситуацию можно объяснить следующим образом. Формулы (4.13)…(4.22) получены с учетом всего двух членов ряда. С ростом числа Био максимальное время уменьшается, вплоть до 0 при .

При очень малых числах Фурье расчёт температур по уравнениям (4.2)…(4.11) затруднителен из-за необходимости учета большого количества членов ряда, ввиду его плохой сходимости. В этом случае для расчёта поверхностной темпе­ратуры можно использовать формулы, полученные методом операционного исчисления в работе 20. Объединяя эти формулы в одно уравнение для простых тел, будем иметь:

, (4.148)

где ; ;

– модифицированное время, число Тихонова;

; — дополнительный интеграл вероятностей;

— функция ошибок Гаусса; ;

— фактор формы, см. уравнение (4.140).

Зная температуру поверхности и используя методику [2], можно найти среднемассовую температуру

(4.149)

где .

При числах для шара или для цилиндра коэффициент и в расчетных соотношениях (4.148) и (4.149) следует раскрывать неопределенность типа . Используя разложение функции при малых аргументах, из уравнения (4.148) получим для температуры на поверхности:

(4.150)

и для среднемассовой из (4.169)

, (4.151)

где и для шара и и для длинного цилиндра.

Таким образом, при малых временах процесса ( ) вместо уравнения (4.6) будет (4.14), вместо (4.8) — (4.14), а температуру в центре тела на начальной стадии нагрева приближенно можно принять .

С учетом сказанного уравнение (4.3) для расчета термических напряжений на поверхности примет вид

. (4.152)

При , после раскрытия неопределенности, получим:

. (4.153)

Дифференцируя уравнение (4.15) по времени и приравнивая производную нулю, можно получить формулу, аналогично (4.10), для расчета времени наступления максимального термического напряжения на поверхности. Ввиду сложности (4.152) и необходимости в дальнейшем решать трансцендентные уравнения, покажем ход расчета на более простом уравнении (4.153). Из соотношения получим квадратное уравнение, решение которого имеет вид:

, (4.154)

где ; ; .

Расчет для шара при и =1 дает , что хорошо согласуется с ранее полученной по (4.10) величиной 0,070318 (см. табл. 4.2).

Иногда требуется определить расположение координаты нейтрального слоя в котором термические напряжения меняют знак с на , т.е. в этой точке равны нулю. Наиболее просто это можно сделать в стадии РРН. Тогда согласно уравнению (4.2)   или . Разрешая последнее выражение относительно , получим

, (4.155)

где .

При малых числах Био . Тогда будем иметь

. (4.156)

При больших числах Био и

. (4.157)

Таким образом, поскольку нейтральные слои расположены ближе к поверхности, а само колеблется в узких пределах от 0,77 до 0,78.

Следует отметить, что при нагреве абсолютные, т.е. размерные термические напряжения поменяют знаки за счет отрицательности из-за .

В заключение укажем, что все полученные решения описывают как процесс конвективного нагрева шаровых тел, так и их охлаждение.

Если расчеты покажут, что максимальные напряжения окажутся больше допустимых, т.е.

_max  _доп, (4.158)

то следует изменить режим или условия нагрева во избежание появления трещин, снижения качества заготовки и т.д.

Графическая иллюстрация безразмерных температурных полей и термических напряжений в максимальные времена их наступления в зависимости от числа Био представлены на рис. 4.1 … 4.6.

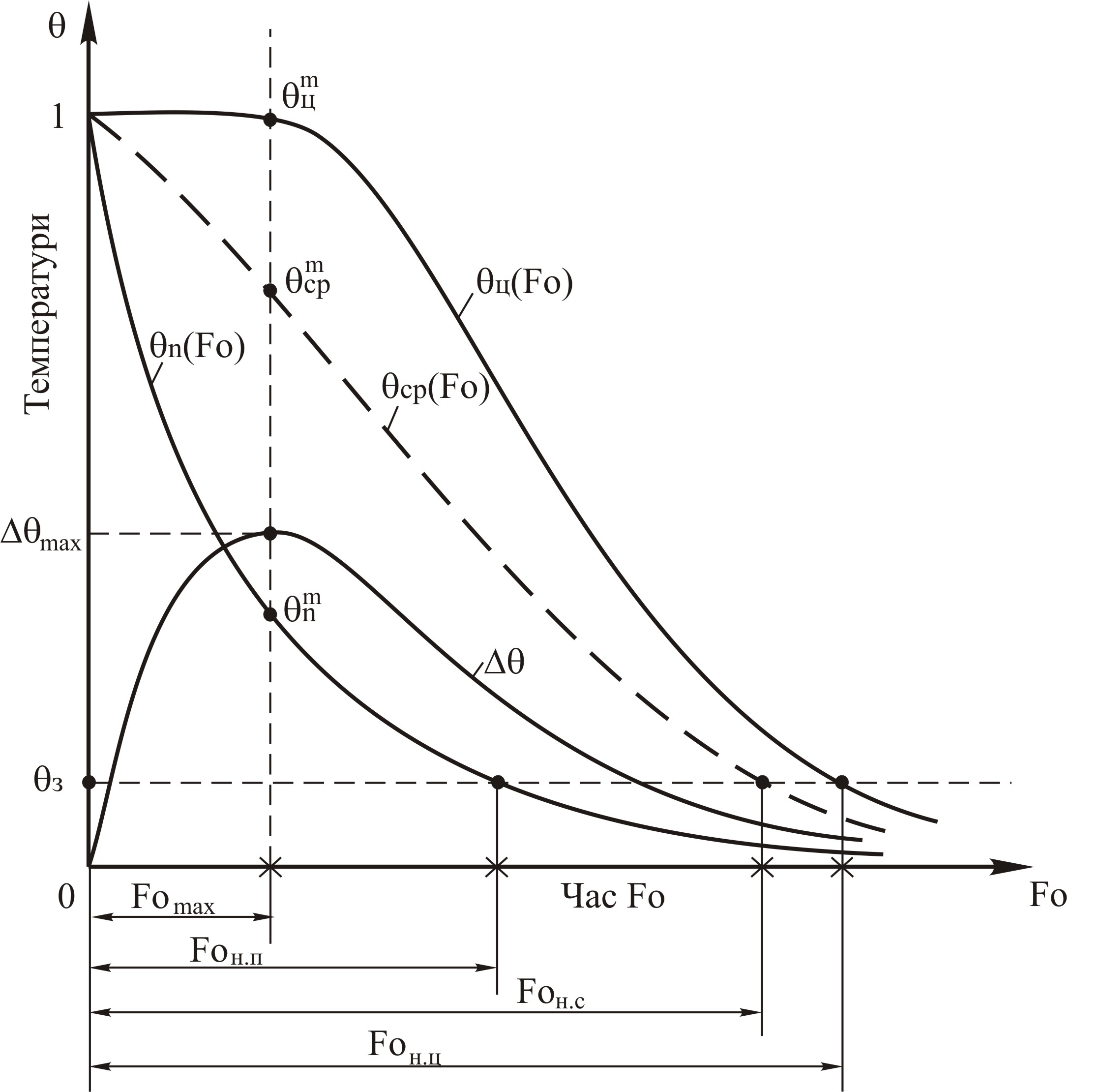
Рис. 4.1.- Динамика изменения безразмерной температуры в центре, среднемассовой, на поверхности и их разности во времени

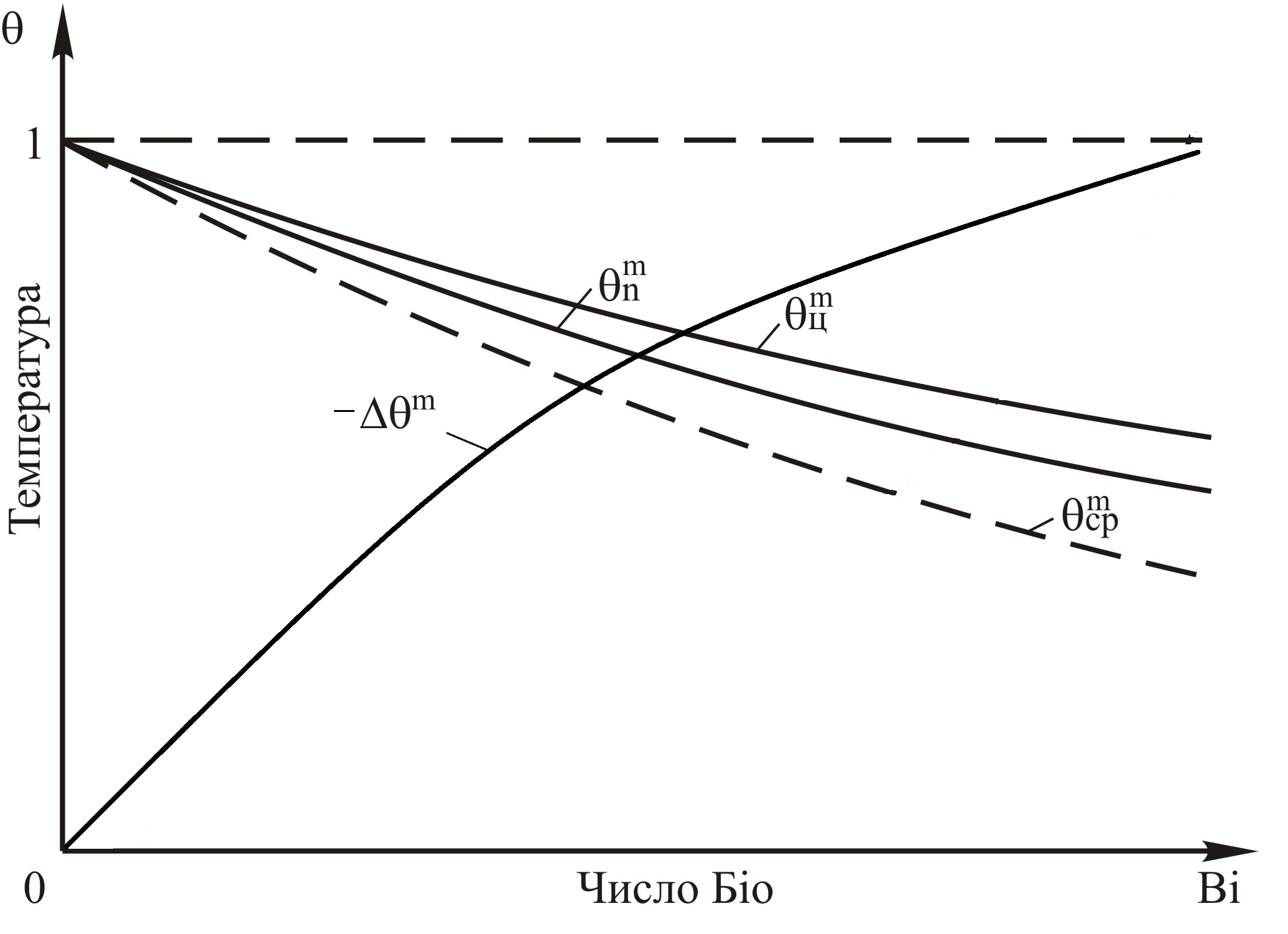
Рис. 4.2. Зависимость максимальных значений Fo_max , , , , от числа Био

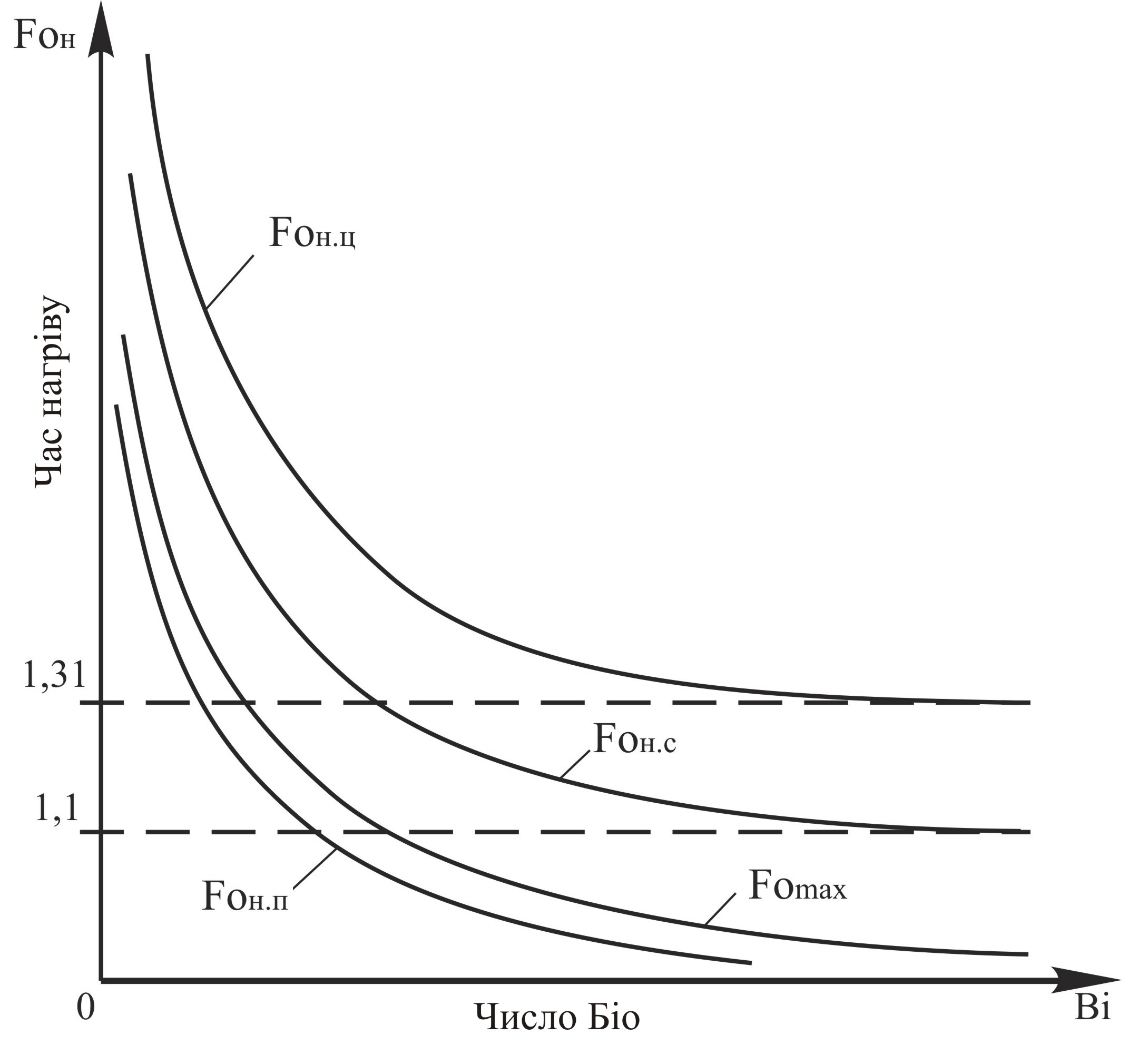
Рис. 4.3. Зависимость времени нагрева тела до заданных температур поверхности, среднемассовой и центра от числа Био

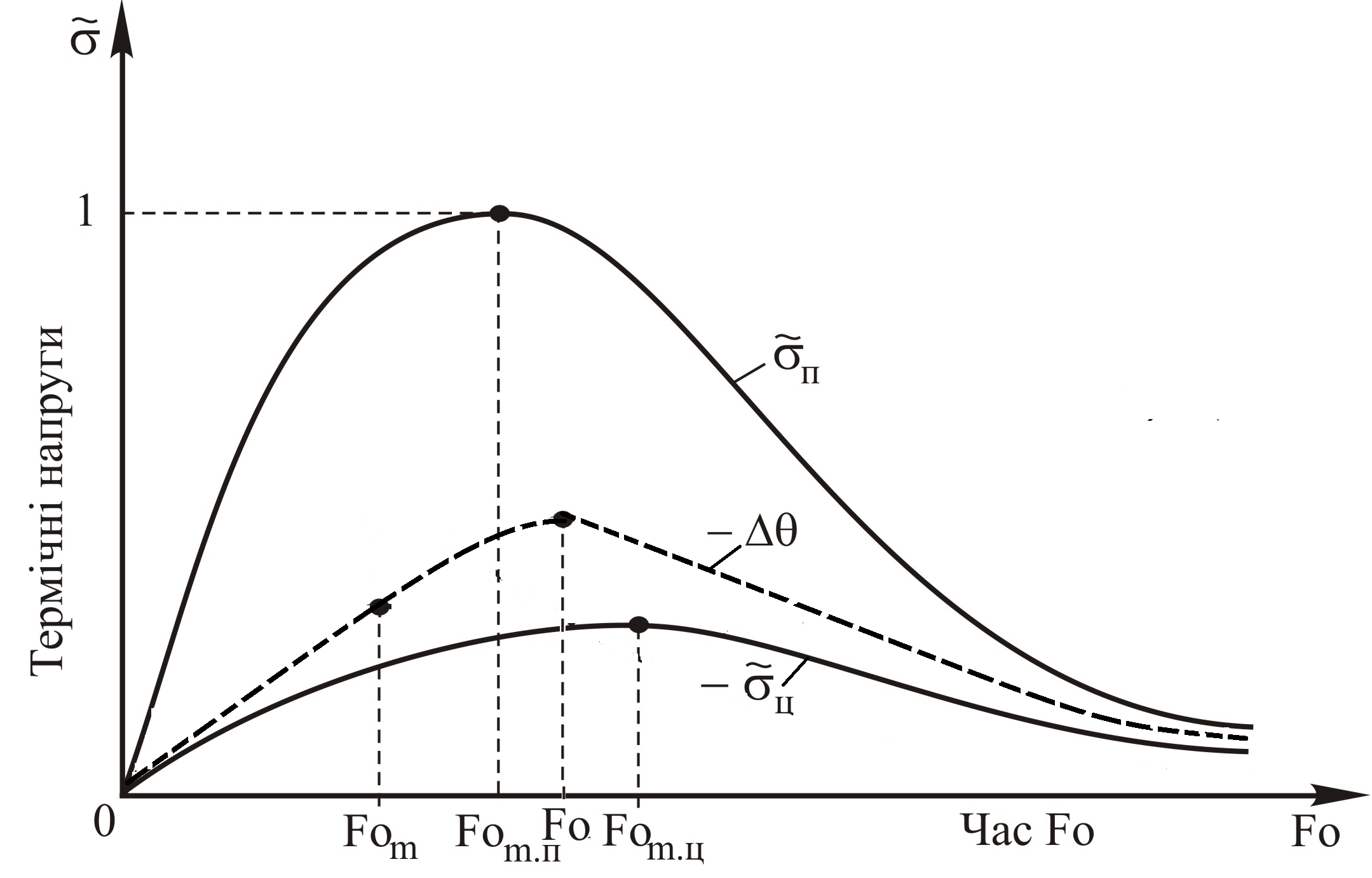
Рис. 4.4. Зависимость безразмерных термических напряжений на поверхности ( ), в центре ( ) и температурной разности ( )

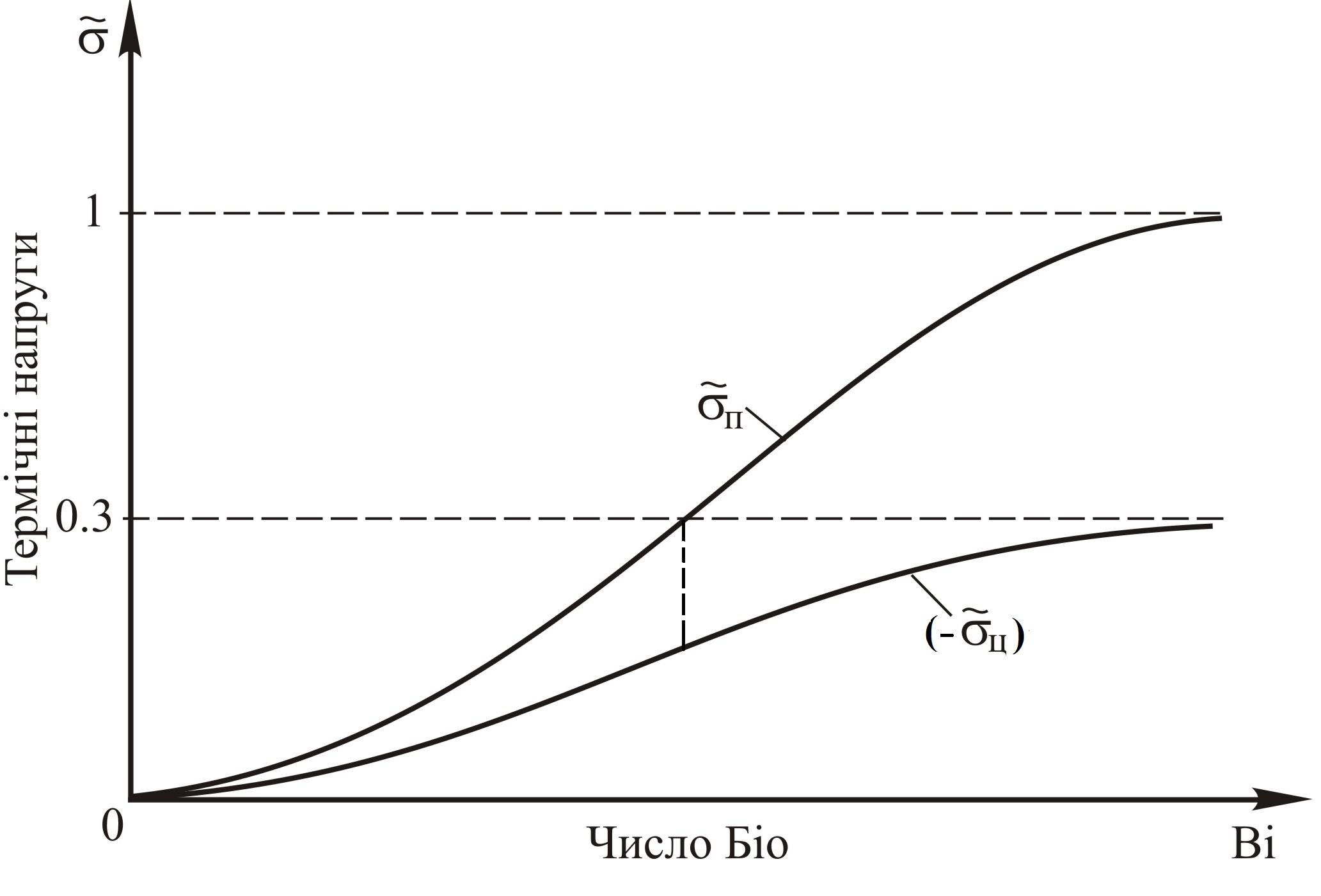
Рис. 4.5. Зависимость максимальных термических напряжений на поверхности ( ) и в центре ( )

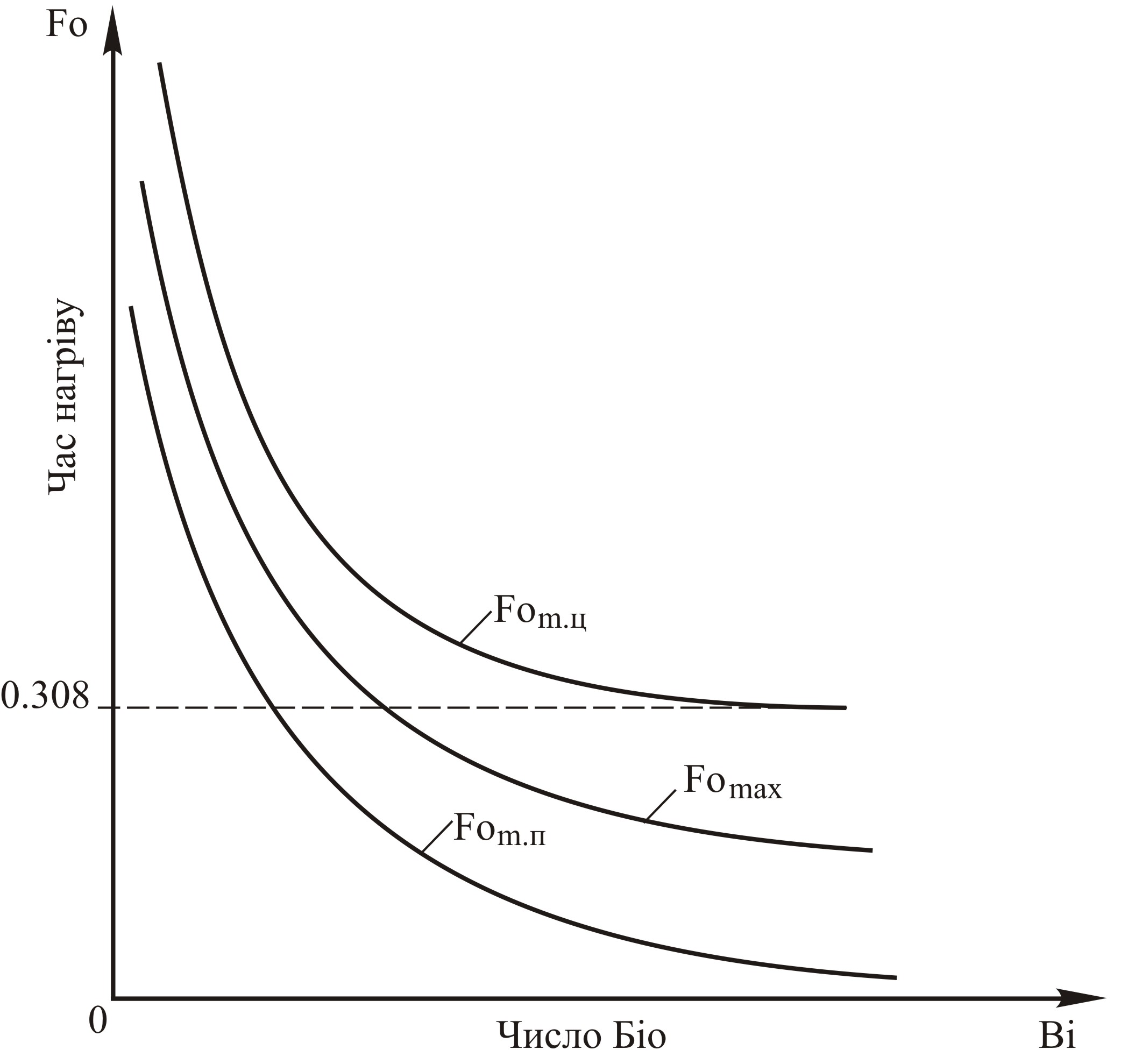
Рис. 4.6. Зависимость времени наступления максимальных напряжений

Fo_m.ц , Fo_max , Fo_m.n от числа Био для пластины