3.2. Влияние числа Био

Физический смысл числа Био можно выявить, переписав его в следующем виде:

.

Получается, что число Био представляет собой отношение внутреннего тер­мического сопротивления к термическому сопротивлению внешней среды. Сле­довательно, число Био является критерием, определяющим интенсивность тепло­вого воздействия среды на процессы нагревания (охлаждения) тела.

На практике часто встречаются два крайних случаев нагрева: при малых и больших числах Био. Рассмотрим их по порядку.

3.2.1 Нагрев термически тонких тел.

Из определения числа Био видно, что его малые значения могут иметь ме­сто в основном при малых размерах толщины пластины, а также при больших значениях коэффициента теплопроводности (нагрев металлов) и малых значе­ниях коэффициента теплоотдачи. Поэтому нагрев тел при малых числах Био (практически при Bi 0,1) принято называть нагревом "термически тонкого" тела (ТТТ). Примеры "термически тонких" тел: консервные банки, рулоны тонколистовых материалов и т.д.

При малых Bi температура на поверхности пластины незначительно отли­чается от температуры на оси. Это указывает на то, что температура по толщине пластины распределяется равномерно и кривая температур остается почти парал­лельной оси Ох для любого момента времени.

Покажем это на анализе полученных выше уравнений.

При малых числах Био уравнение (3.10) для определения первого корня пре­образуется к виду

, (3.37)

где - коэффициент термической массивности тела.

Начальная тепловая амплитуда с учетом (3.37) станет

. (3.38)

При весьма малых числах Био, используя приемы прикладной математики, например дробь, или при малых , получим

. (3.39)

Амплитуда для расчета среднемассовой температуры при малых Био запишется в форме:

. (3.40)

Центральная амплитуда для расчета температур в центре пластины с учетом разложения косинуса в ряд при малых аргументах упрощается до вида:

. (3.41)

Погрешность формулы (3.41) можно значительно уменьшить. Применяя тригонометрическое выражение и используя характеристическое уравнение (3.5), получим

. (3.42)

Тогда более точная формула будет иметь вид

. (3.43)

С учетом уравнений (3.37) и (3.39) основное уравнение (3.4) для термически тонкого тела (ТТТ) запишется в форме:

(3.44)

Так как произведение

то уравнение (3.44) можно записать в виде:

(3.45)

Отношение служит мерой тепловой инерции термически тонкого тела. Обратная величина может быть названа постоянной времени пла­стины Т; она часто применяется в теории автоматического регулирования и чис­ленно равна промежутку времени, за которое максимальный температурный на­пор "погасится" на 63,2%, так как при нагреве

.

Среднемассовая температура тонкого тела совпадает с текущей температу­рой, т.е. определяемой уравнением (3.45).

Время нагрева ТТТ до заданной температуры (3.32) можно определить по уравнению (3.33) при , и , а именно:

. (3.46)

При практических расчетах полезно знать: завышение или занижение температуры будет давать модель ТТТ по сравнению с точным решением. Так как температура тонкого тела примерно совпадает с а , то естественно сравнивать расчет по ТТТ со среднемассовой температурой термически массивного тела. Составим отношение времени нагрева массивного тела ко времени нагрева по модели ТТТ. Тогда с учетом уравнений (3.35) и (3.45) получим

.

Таким образом

(3.47)

и так как коэффициент термической массивности всегда больше 1, то будет больше, чем время нагрева по модели ТТТ. Следовательно , а размерные (в ) температуры, рассчитанные по модели ТТТ будут завышены при нагреве (занижены при охлаждении) по сравнению с точным решением для среднемассовой температуры.

Решение (3.46) позволяет найти такое граничное число , когда тело можно считать термически тонким. Если задаться погрешностью расчетов П₁ (%), то из неравенства с учетом (3.46) вытекает, что

. (3.48)

Из уравнения (3.48) следует, что если при расчетах времени нагрева приемлема или достаточна погрешность П₁=5%=0,05, то , а если 10%, то и т. д.

Оценим вторым способом погрешность, которую вносит использование модели термически тонкого тела. О малой погрешности можно судить по малости разности темпера­тур поверхности и середины пластины . Для случая регулярного ре­жима нагрева согласно уравнению (3.16)

. (3.49)

Из уравнения (3.49) можно видеть, что разность температур пропорцио­нальна первоначальной максимально возможной разности температур среды и тела t₀, с течением времени существенно уменьшается по экспоненциальному закону. Формула (3.49) неудобна для оценки погрешности из-за зависимости от времени, однако, если ввести относительную разность температур поверхно­сти и центра, т.е. отнести ее к средней температуре тела, то можно получить формулу, независящую от числа Фурье:

(3.50)

При выводе (3.50) было учтено, что согласно (3.37) и применено раз­ложение косинуса в ряд при малых аргументах.

Из уравнения (3.50) следует, что если при расчетах по модели ТТТ достаточна погрешность П₂=5%, то число Био должно быть

а если 10%, то и т.д.

По рекомендации ученых уральской школы металлургических теплотехников, с погрешностью, приемлемой в инженерных расчетах можно пользоваться формулами (3.44)…(3.46) даже при Bi 1, если ввести в них поправочный коэффициент 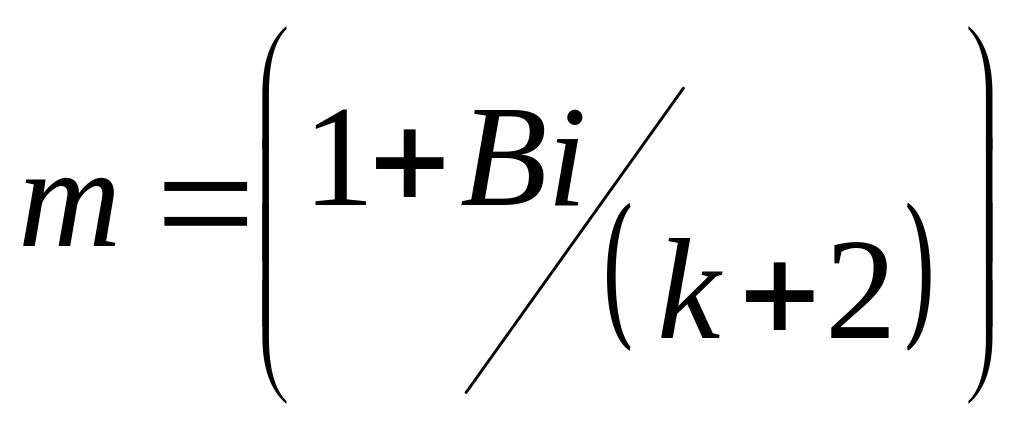, учитывающий термическую массивность тела; где k – коэффициент формы тела (см. уравнение (3.28)). Тогда в уравнениях (3.44)…(3.46) следует заменить число Био на .

Заметим, что коэффициент термической массивности автоматически выте­кает из уравнения (3.9), если его записать в виде

, (3.51)

т. е. коэффициент массивности есть не что иное как отношение числа Био к квадрату первого корня уравнения (3.5):

. (3.52)

Тогда из уравнения (3.9) с учетом (3.52) можно получить уточненное значение коэффициента термической массивности:

, (3.53)

где ; .

Максимальная погрешность в определении коэффициента массивности или первого собственного числа будет наблюдаться при бесконечно большом числе Био. Точное значение первого корня при (см. уравнение (3.12)). Расчет по уравнению (3.51) дает с погрешностью , а использование формулы (3.53) приводит к и . Таким образом, использование уточненного значения коэффициента массивности, вместо общепринятого, примерно в 16 раз уменьшает погрешность расчетов при больших числах Био. Тогда в формулах модели ТТТ следует заменить число Био на .

Для расчета времени инерционного периода при малых числах Био воспользуемся уравнением (3.30). Полагая в последнем и разлагая функцию ошибок в ряд при малых аргументах согласно [20] , а также , получим постоянную

æ_{1 ..} (3.54)

Окончательно, используя выражение (3.29), время инерционного периода

æ₂/Bi² , (3.55)

где æ₂ =1/(4æ₁²)= .

Время можно найти вторым способом из уравнения (3.35) при :

. (3.56)

При малых числах Био уравнение (3.56) с учетом (3.41) и разложения упрощается до вида

æ/Bi, (3.57)

что качественно хорошо согласуется с результатом (3.55), полученным другим способом.

Оценим температурное поле в момент времени , когда температура в центре пластины . Из уравнения (3.57) следует, что при малых числах Bi Bi_т =0,15 и æ₃ число будет больше 1/3 и можно пользоваться формулами для стадии РРН.

Согласно уравнению (3.21) в любой момент времени регулярного режима температура поверхности связана с температурой центра следующей зависимостью

(3.58)

В конце инерционного периода

. (3.59)

Аналогично имеем из (3.22) для среднемассовой температуры

(3.60)

и в момент времени

. (3.61)

В заключение оценим погрешность модели ТТТ третьим способом. Составим для стадии РРН относительную разность среднемассовой температуры и тонкого тела, т. е. вычтем (3.44) из уравнения (3.22)

.

Анализ П₃ показал, что эта функция имеет колоколообразный характер с максимумом в точке , который можно найти путем дифференцирования П₃ по числу Фурье и приравнивания производной нулю, а именно:

, (3.62)

где .

После подстановки , а точнее в П₃ получим максимально возможную относительную погрешность, которая будет получаться при использовании модели ТТТ

. (3.63)

Уравнение (3.63) подтверждает вывод, сделанный при анализе уравнения (3.48) о том, что граничное число Био для модели тонкого тела должно быть меньше утроенной погрешности .

Для оценки диапазона работоспособности полученных предельных соотношений для ТТТ приведен расчет по формулам (3.37)…(3.43) при Bi=1. Тогда или более грубо , , и . Сопоставление с точными табличными данными [20] показало следующие погрешности : и 26%, и 8,7%, и 9,9%, и 4,2%.

Таким образом, максимальные погрешности наблюдаются при расчетах М₁ и не превышают 2% (26% при грубых оценках ) даже при Bi=1, которое значительно больше . Поэтому, если учитывать коэффициент массивности (3.52) или (3.53) и вести расчет по уравнениям (3.38), (3.40) и (3.43), то можно считать .

Перейдем к рассмотрению другого предельного случая.