Анализ полученного решения

Во-первых, решение (3.4) пригодно для расчётов не только процессов нагрева, но и для процессов охлаждения. Кроме случаев расчета температурной разно­сти (_п - _ц), когда при нагреве следует вместо  применять

= 1-  = (t – t₀) / (t_ж – t­₀).

Из уравнения (3.4) вытекает, что температура зависит от времени процесса, числа Био и координаты тела.

Рассмотрим последовательно влияние указанных величин.

Технологов и практиков, как правило, интересует не всё температурное поле, а только температуры пластины в крайних точках: на поверхности и в центре. Полагая в уравнении (3.4) последовательно и , получим для безразмерной температуры на поверхности

(3.14)

и в центре пластины

, (3.15)

где .

Значительный практический интерес представляет температурная разность между поверхностью и центром, поскольку термические напряжения, возникающие при нагреве тела, прямопропорциональны этой разности. Вычитая из уравнения (3.14) выражение (3.15), получим безразмерную разность температур

, (3.16)

где .

В работах ученых Днепропетровской школы металлургических теплотехников, например, [7] и др., широко применяются при инженерных расчетах нестационарных тепловых процессов коэффициенты усреднения теплового потока

(3.17)

и температуры

. (3.18)

Как правило, коэффициент используется для расчета температурной разности , а коэффициент - среднемассовой температуры .

3.1 Влияние времени

3. 1. 1 Регулярный режим нагрева

Так как последовательность представляет собой ряд воз­растающих (примерно на величину равную трём, так что _n+1_n+3) чисел, то чем больше , тем меньше роль последующего члена ряда в уравнении (3.4) по сравнению с предыдущим. Кроме того, с течением времени и чем больше будет число Фурье, тем члены ряда будут убывать быстрее с увеличением номера . Многочисленные исследования показали, что уже при ряд (3.4) быстро сходится и ошибка не превышает 1%, если отбросить все члены ряда, кроме пер­вого. При этих условиях уравнения (3.4), (3.14), (3.15) примут вид:

, (3.19)

температура на поверхности

, (3.20)

и в центре пластины

. (3.21)

Зависимость (3.7) для определения среднемассовой температуры также упро­щается

. (3.22)

Логарифмируя уравнение (3.20), получаем выражение

ln_n = lnP₁ - ₁²Fo, (3.23)

из которого следует, что при заданном значении координат (поверхность, центр или среднемассовая температура) и при известном числе Био натуральный ло­гарифм безразмерной температуры линейно зависит от времени. Последнее об­стоятельство дает возможность представить для уравнений (3.20)…(3.22) простое графическое решение в полулогарифмических координатах ln_ц = f₁ (Fо) – рисунок 3.2 и ln_n = f₂ (Fо) – рисунок 3.3 в виде семейства прямых линий при различных числах Bi.

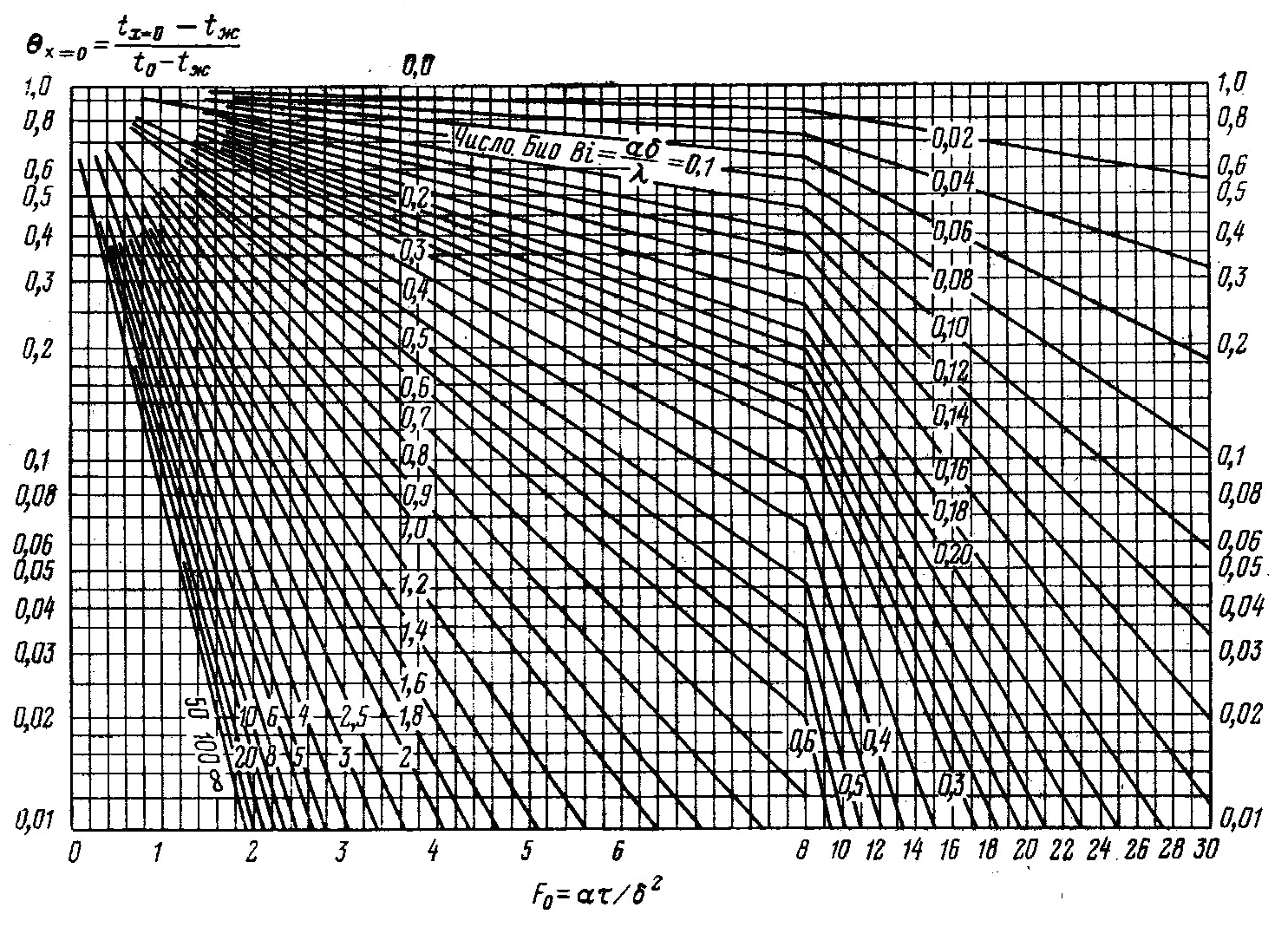
Рисунок 3.2- Зависимость для середины пластины

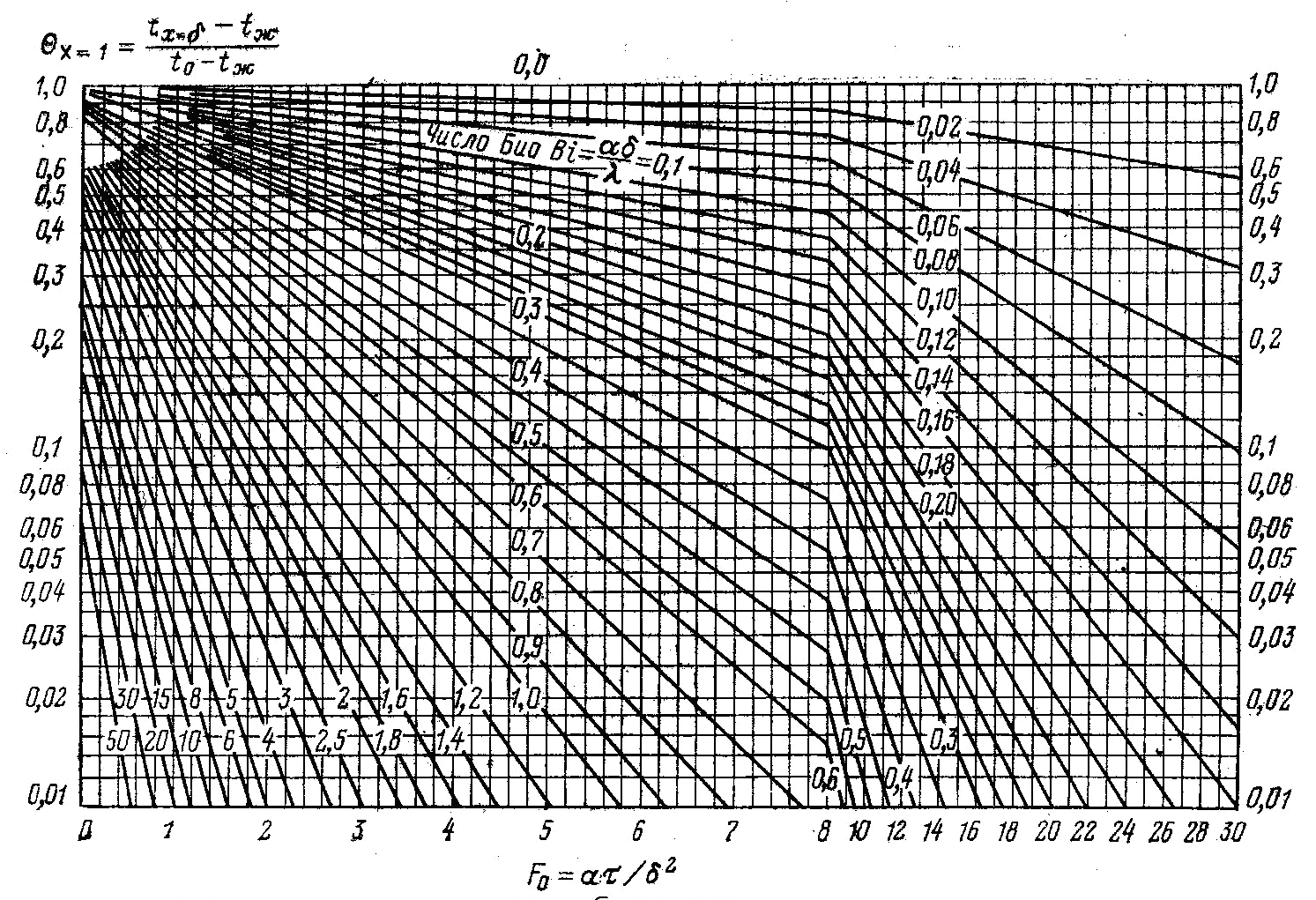
Рисунок 3.3.- Зависимость для поверхности пластины

Физически нагрев тела при больших числах Фурье принято назы­вать регулярным или квазистационарным режимом нагрева (охлаждения).