3. Решение задачи

Уравнение (2.1) является параболическим уравнением математической физики в частных производных, второго порядка. Поскольку дифференциальные уравнения (2.1)…(2.4), которые описывают процесс теплопроводности в теле простой формы линейные, можно получить точное аналитическое решение, применяя классический метод Фурье, т.е. метод разделения переменных 20.

Представим, что температура определяется произведением двух функций, одна из которых зависит только от пространственной координаты, а вторая  только от времени. Это эквивалентно введению следующей замены перемен­ных:

. (3.1)

Дифференцируя (3.1) по времени и дважды по координате, а затем подставляя в уравнение (2.1), получим

. (3.2)

Известно, что две функции от двух разных и независящих друг от друга аргу­ментов могут быть равны при любых значениях последних только в том случае, если они равны одной и той же постоянной величине, равной, например –k². Тогда из выражения (3.2) вытекает два уравнения

Решением последних будет

,

.

Подставляя U и V в уравнение (3.1), получим:

(3.3)

Постоянные интегрирования С, D и k находим из начального (2.2) и гранич­ных условий (2.3) и (2.4). Подробный вывод приведён в 20].

Окончательно решение уравнения (3.3) в безразмерной форме, согласно [3] имеет вид:

, (3.4)

где  безразмерная, относительная температура, 0≤θ≤1;

— первоначальная, максимально возможная разность температур, ⁰С;

 безразмерная координата, ;

 безразмерное время, число Фурье;

 тепловая амплитуда;

 число Био;

 характеристические числа, которые находятся из следующего трансцендентного уравнения:

. (3.5)

Из анализа уравнения (3.5) видно, что имеет бесчисленное множество значений. Наиболее просто можно определить корни уравнения (3.5) графическим путем. Если левую часть уравнения обозначить через , а правую часть — через , то пересечения котангенсоиды с прямой (рис. 3.1) дают нам значения корней характеристического уравнения. Из рис. 3.1 видно, что имеется бесчисленное множество корней , причем каждое последующее решение больше предыдущего:

Чем больше n, тем ближе к числу .

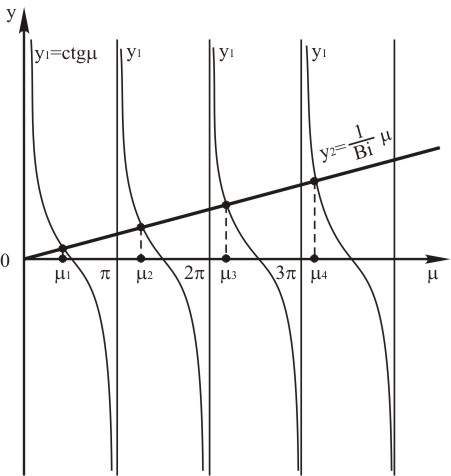
Рисунок 3.1- Графический способ определения корней характеристического уравнения

Количество тепла, пошедшего на нагрев, можно найти по формуле

, (3.6)

где m  масса тела, кг;

 среднемассовая или среднеинтегральная температура, .

В соответствии с теоремой о среднем:

или в безразмерном виде

, (3.7)

где .

С учётом формулы (3.7) уравнение (3.6) можно записать в виде:

, Дж, (3.8)

где — полное или максимально возможное количество теплоты, которое воспринимает или отдаёт пластина с обеих сторон за период полного её нагревания (охлаждения) от до .

Наибольшую и основную трудность при практических расчётах температур­ного поля по уравнениям (3.4) и (3.7) представляет определение бесчисленного множества корней , которые находятся из уравнения (3.5). Первые шесть кор­ней уравнения (3.5) с точностью до четвёртого знака приведены в 20 для дис­кретных значений числа Био, изменяющегося от 0 до .

Однако проведение расчётов по формулам (3.4) и (3.7) с использованием табличных значений корней весьма затруднительно. Поэтому воспользуемся результатами работы 3, в которой приведены формулы по аналитическому определению корней уравнения (3.5).

Согласно 3, приближённое значение первого корня уравнения (3.5) было получено путём разложения в ряд

, .

Подставляя последнее в уравнение (3.5) и решая биквадратное уравнение, получим

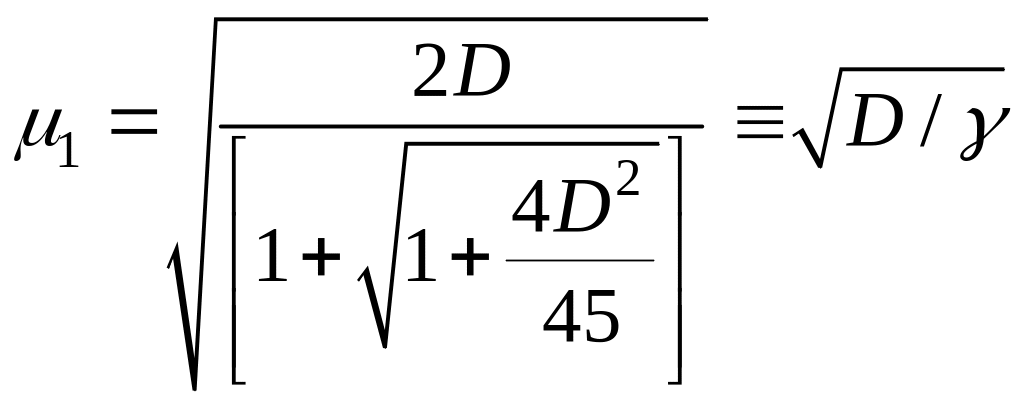, (3.9)

Где ; -коэффициент термической массивности тела; ; . При малых : .

Уравнение (3.9) при достаточно малых числах Био, когда , упрощается до следующей зависимости

. (3.10)

Для определения приближённых значений остальных корней следует разли­чать два характерных случая нагрева  при больших и малых числах Био.

Оказалось, что при малых числах Био

, (3.11)

где ; ; ,

а при больших числах Био ( )

, (3.12)

где - корни характеристического уравнения (3.5) при Bi= ; ; ; β=1/ Bi.

Формулы (3.9)…(3.12) являются приближёнными и при больших требованиях к точности расчётов необходимо уточнить эти решения. Применяя к трансцендентному уравнению (3.5) метод касательных Ньютона [6] для расчета (k + 1)-ого приближения

где ; , получим уточняющее уравнение

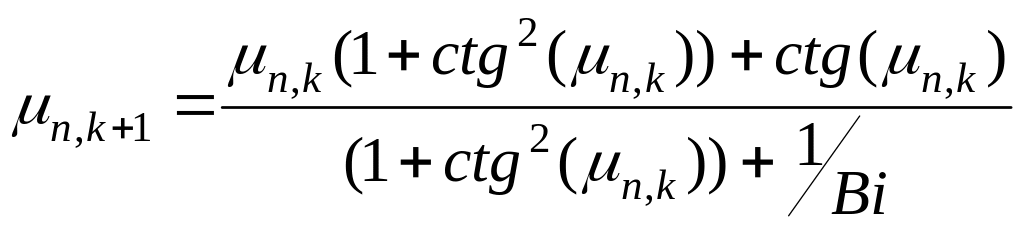, (3.13)

где в качестве k-того приближения берётся любой корень, полученный из приведённых выше формул (3.9)…(3.12).

Расчёт по уравнению (3.13) можно прекратить при выполнении условия , где   малое число, например, =0,00001. Обычно доста­точно не более трёх итераций, а для номера корня необходимость в ите­рациях отпадает.