2. Нестационарная теплопроводность. Расчет температурных полей

Одной из основных задач теплотехники, в том числе и металлургической, яв­ляется определение продолжительности теплового процесса, например, нагрева металла в печах, динамики процесса затвердевания слитков (отливок), плавле­ния тел в мартеновской печи или конвертере, прогрева футеровки ковшей, печ­ных стенок и т. п.

Данный класс задач невозможно решить без определения пространственно-временного распределения температуры или температурного поля внутри тела в нестационарном тепловом процессе.

Без знания полей температур и термических напряжений внутри массивного тела невозможно назна­чить рациональные энерго- и материалосберегающие тепловые и температур­ные режимы печей или других агрегатов, связанных с тепловой обработкой ма­териалов, например, сушильных установок, химических реакторов и т. п.

2.1 Физическая постановка задачи

Дано:

Пластина толщиной , гораздо меньшей её высоты и ширины с начальной равномерной (одинаковой) по толщине температурой помещена в печь или другое пространство, имеющее постоянную температуру , и там нагревается при неизменном коэффициенте теплоотдачи (рис. 2.1). Внутренние источники (стоки) тепла отсутствуют. Здесь и далее под жидкостью будем понимать как жидкость в буквальном смысле, так и газы.

Требуется найти:

Температурное поле, т. е. температуры в любой момент вре­мени в любой точке пластины, время нагрева её до заданной температуры по­верхности , количество тепла, пошедшего на нагрев и термические напряжения.

2. Математическая постановка задачи

Поместим начало координат на оси симметрии пластины. Вследствие

симметрии процесса нагрева будем искать температурное поле для правой поло­вины пластины толщиной .

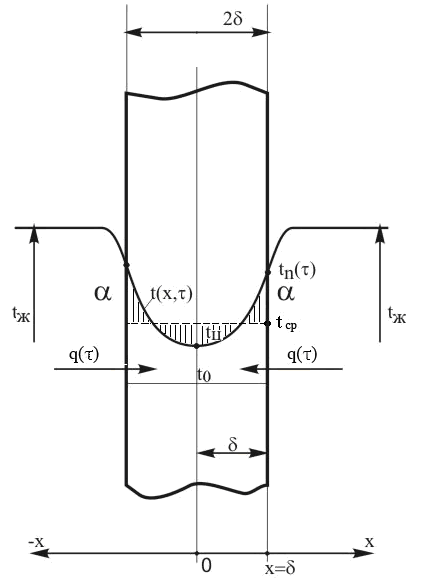
Рис. 2.1- К постановке задачи теплопроводности в пластине

Если пластина нагревается с одной стороны, а другая сторона изолиро­вана, например, при нагреве заготовок, лежащих на подине печи, то ее можно рассматривать, как половину пластины; при этом изолированная сторона будет соответствовать середине пластины. Следовательно, за расчетную толщину пластины следует в этом случае принимать ее полную толщину.

При рассмотрении процессов теплопроводности необходимо использовать дифференциальное уравнение переноса тепла. Так как тело плоское, исполь­зуем дифференциальное уравнение теплопроводности в декартовой системе ко­ординат

,

где  время процесса, с;

 искомая температура, ;

 массовая теплоёмкость, Дж/кгК;

 плотность, кг/м³;

 коэффициент теплопроводности, Вт/мК.

Для простоты задачу будем решать в линейной постановке, т. е. при постоян­ных, независящих от температуры теплофизических свойствах. Ввиду малости толщины пластины по сравнению с её высотой и шириной можно пренебречь осевыми и продольными растечками тепла.

С учётом сказанного дифференциальное уравнение теплопроводности для данной задачи примет вид:

, , (2.1)

где  коэффициент температуропроводности, м²/с.

К уравнению (2.1) следует добавить краевые условия или условия однозначности:

— начальное условие

(2.2)

— и граничные условия на:

• левой (2.3)

• правой границе , (2.4)

где  температура на поверхности пластины, .

Уравнение (2.3) вытекает из условия симметрии или адиабатности на оси (см. рис. 2.1).

Система дифференциальных уравнений (2.1)…(2.4) представляет собой математи­ческую постановку рассматриваемой задачи.