1.5.6 Теплопроводность многослойной цилиндрической стенки

Заданы температуры на внутренней и наружной поверхностях стенки. Требуется найти t(r) и тепловой поток (рис.1.10).

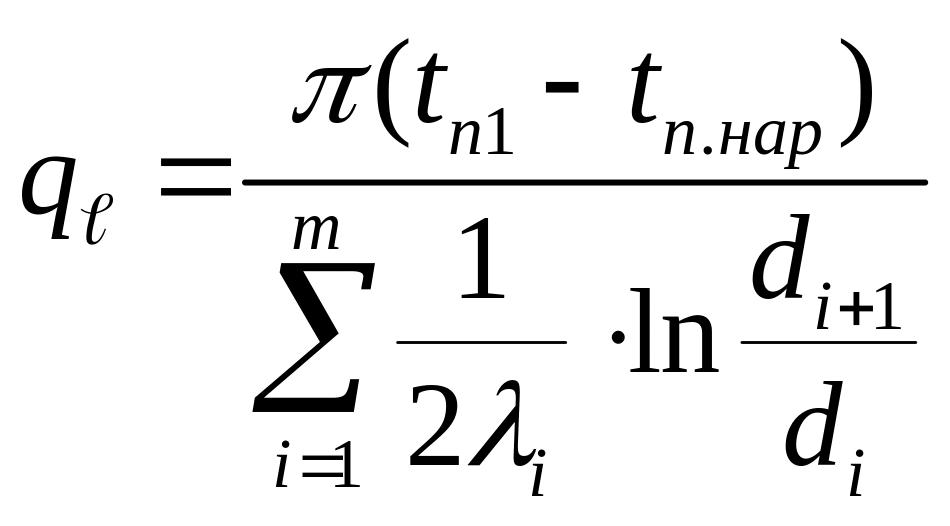, сразу запишем , Вт/м. (1.30)

Температуру t(r) в любой внутренней точке тела можно найти по уравнению (1.26) аналогично расчету по (1.19) для многослойной плоской стенки – см. раздел 1.5.2.

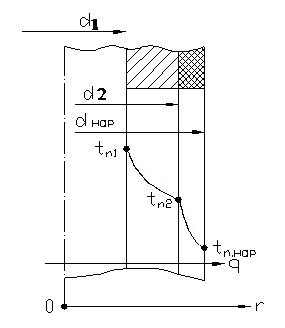
Рис. 1.10. Теплопроводность цилиндрической многослойной стенки

Температуру в местах контакта стенок найдем из выражения (1.27) для потока тепла через интересующую нас стенку : ,

где - термическое сопротивление i-той цилиндрической стенки.

1.5.7 Теплопередача через цилиндрическую однослойную стенку

Дано: и . Найти : t(r), q, , (рис.1.11).

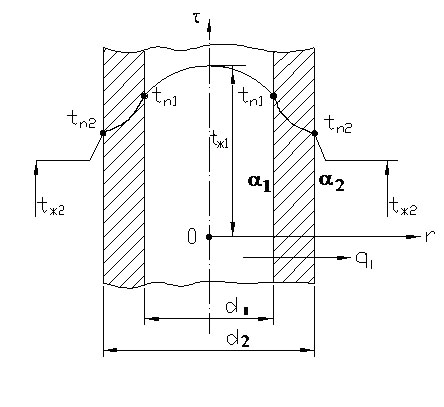
Рис. 1.11. Теплопередача через однослойную цилиндрическую стенку

Сразу запишем

, (1.29)

где .

К_ – линейный коэффициент теплопередачи Вт/мК.

Температуру на левой поверхности найдем из закона теплоотдачи , т.е. . Аналогично температура на правой поверхности из , либо .

Анализ: в сравнении с плоской стенкой, когда или  d₂ ,

то

и .

1.5.8. Теплопередача через многослойную цилиндрическую стенку

Многослойка , m-слоев, рис. 1.12. Сразу запишем , (1.30)

где , .

Температура на левой поверхности и наружной

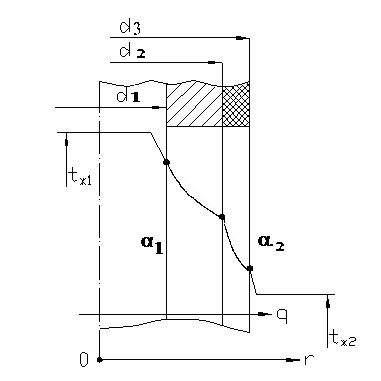
Рис. 1.12 Теплопередача через многослойную цилиндрическую стенку

1.5.9. Критический диаметр тепловой изоляции

ОПРЕДЕЛЕНИЕ. Тепловая изоляция - это всякое покрытие горячей поверхности, которое способствует снижению потерь теплоты в окружающую среду.

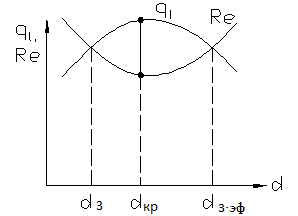
Рис. 1.13. Зависимость тепловых потерь от толщины изоляции, наложенной на цилиндрическую стенку

Термическое сопротивление такой стенки

.

Здесь оказалось, что количество не всегда пропорционально качеству, т.е. рост толщины изоляции не всегда уменьшает тепловые потери в окружающую среду.

Исследуем функцию термического сопротивления на экстремум (Рис. 1.13). Для этого берем производную по диаметру изоляции и приравниваем ее нулю.

.

Окончательно . (1.31)

Если будет то изоляция не эффективна. Должно быть: .

Для других стенок, кроме плоской, можно получить аналогичные решения.

1.5.10. Теплопередача через шаровую стенку

Для шара: Поле температур t(r)= C₁ - C₂ /r . Тепловой поток:

,Вт, (1.40)

где ; ; .

Термические напряжения в шаровых стенках также определяется по уравнением (1.11) и (1.12). С учетом того, чтоб объем шара уравнение (1.18) преобразуется к виду

. (1.41)

Подставляя в уравнение (1.44) решение (1.17) для поля температур в шаровой стенке в виде

, (1.42)

где - средний радиус стенки, м;

.

При малых перепадах температур :

1.5.11. Теплопередача через стенки неправильной формы

Способы усреднения поверхности нагрева:

- среднеарифметическое ;

- среднелогарифмическое 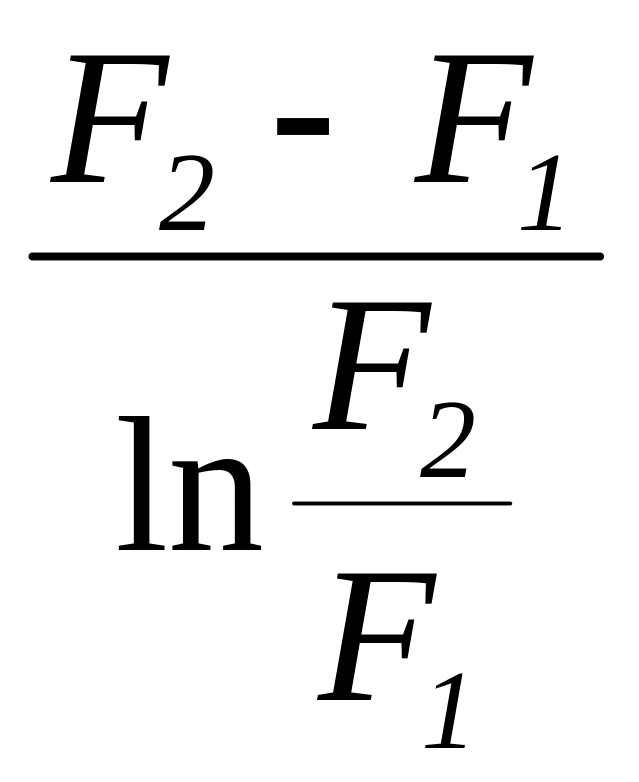; (1.33)

- среднегеометрическое ;

где F₁ – внутренняя, F₂ – внешняя поверхность, .

Средняя температура поверхности 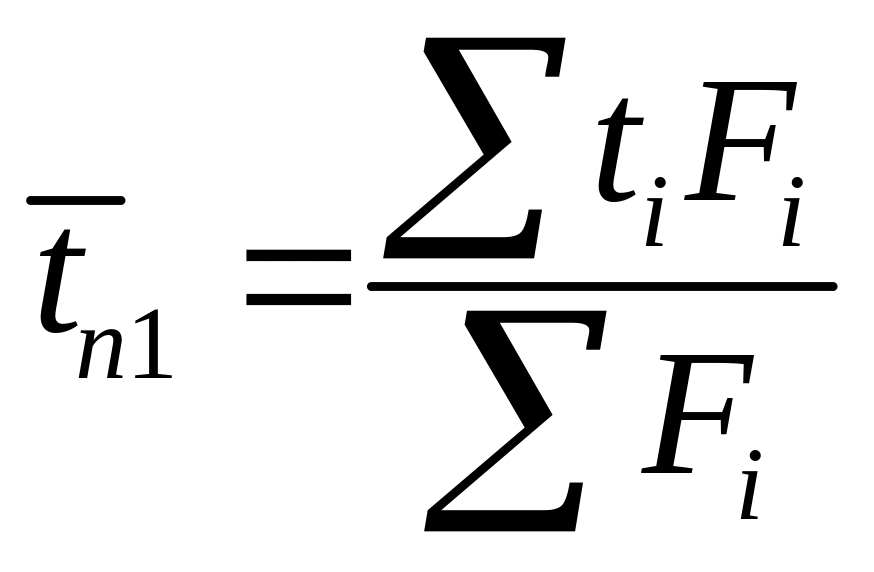; 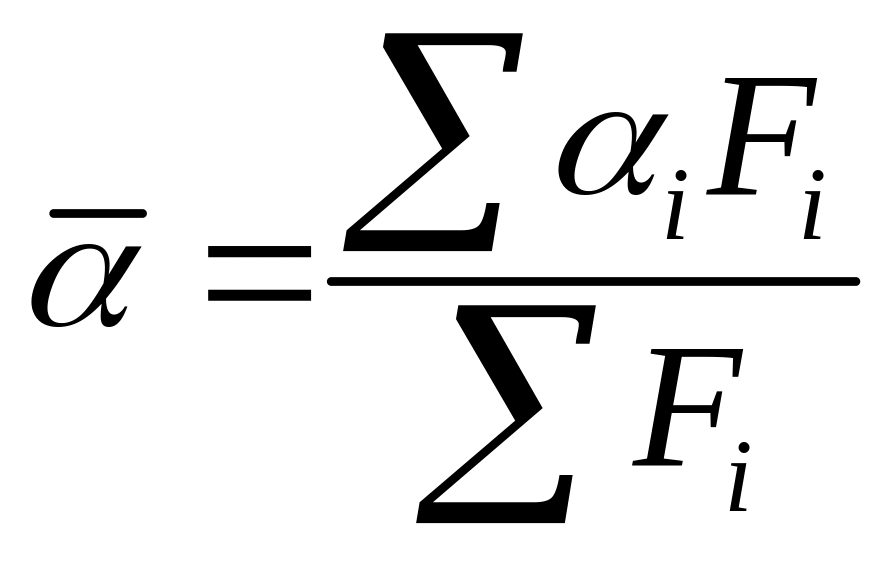–усредненный по поверхности коэффициент теплоотдачи. Тепловой поток .

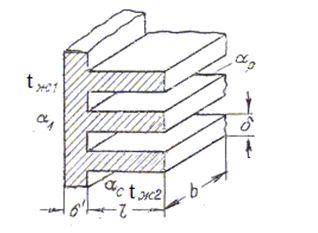
Рис. 1.14 Теплопередача через ребристую стенку

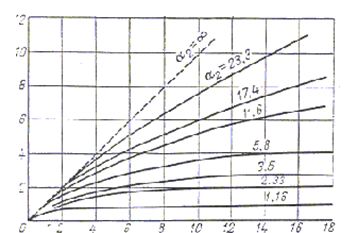
Рис. 1.15 Зависимость К=f ( α_{1 ,} α₂)