1.3.Нестационарные процессы теплопроводности
1.3.1.Физическая сущность процессов
Это такие процессы теплопроводности, когда поле температуры в теле изменяется не только в пространстве, но и во времени. Они имеют место при нагревании и охлаждении заготовок, пуске и остановке различных тепло-обменных устройств и т.д.
Среди практических задач нестационарной теплопроводности важней-шее значение имеют две группы процессов:
1.тело стремится к тепловому равновесию;
2.температура тела претерпевает периодические изменения.
К первой группе относятся процессы нагрева или охлаждения тел, помещенных в среду с заданным тепловым состоянием. Например, тело внесено в среду с более высокой температурой. Сразу же между телом и средой возникает процесс теплообмена, тело начинает прогреваться, а его температура повышается.
Ко второй группе относятся процессы в периодически действующих подогревателях, например, тепловой процесс регенераторов, насадка которых периодически то нагревается дымовыми газами, то охлаждается.
Количество передаваемой теплоты при нестационарном режиме во времени также непостоянно. По мере прогрева тела количество воспри-нимаемой теплоты сначала увеличивается, достигает максимума, затем уменьшается и в пределе при тепловом равновесии становится равным нулю.
Нагревание или
охлаждение тел сопровождается непрерывным
изменением температуры внутри этих тел
и на их поверхностях и по своей физической
сущности связано с изменением
теплосодержания. Так как скорость
изменения теплосодержания прямо
пропорциональна способности материала
проводить теплоту, т.е. коэффициенту
теплопроводности
и обратно пропорциональна его
аккумулирующей способности, т.е. объемной
теплоемкости
,
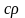то в целом скорость нагревания или
охлаждения тела при нестационарном
режиме определяется значением
коэффициента температу-ропроводности
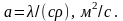
1.3.2.Решение дифференциального уравнения теплопроводности в критериальном виде
Сложность расчета температурного поля связана с наличием большого числа факторов, влияющих на процессы нагрева или охлаждения тел. Пользуясь методами теории подобия, уравнение температурного поля можно представить в критериальном виде и тем самым значительно сократить число независимых переменных. Это позволяет упростить расчеты.
В качестве примера
рассмотрим нагрев пластины толщиной
,
имеющую одинаковую температуру по
сечению
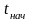(рис.1.9).
Плита помещена в печь, температура
которой
Она обогревается с обеих сторон
одинаково, причем коэффициент теплоотдачи
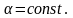Коэффи-циенты
и
также постоянны. Для данных условий
можно записать:
(1.41)
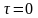При
и
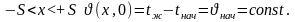(1.42)
При
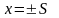
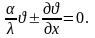(1.43)
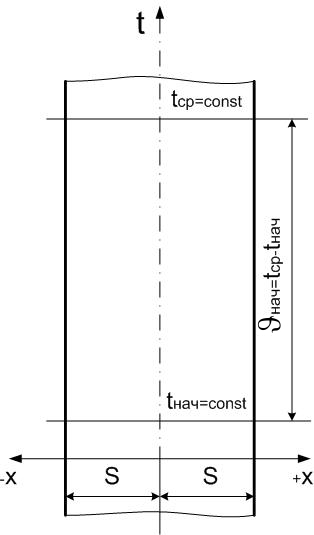
Рис.1.9.К случаю нагрева плоской неограниченной стенки
Уравнения (1.42) и
(1.43) определяют собой краевые условия
задачи. Во всех уравнениях
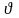означает избыточную температуру. Так
,
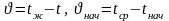где
- температура какой-либо точки пластины
в какой-то момент времени.
Из уравнений (1.41) - (1.43) следует, что
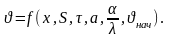(1.44)
В этом уравнении
количество размерных величин N
=7, а число единиц измерения (м, с, оС)
k=3.
На основании
-
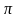теоремы можно сделать предположение
о том, что критериальное уравнение
должно содержать 4 критерия, или симплекса,
так как N-k=4.
При любой системе
единиц математическая формулировка
физии-ческого процесса должна оставаться
справедливой. Поэтому изменим масштабы
единиц измерения. Изменим единицы
измерения длины в
,
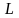времени в
,
а температуры в
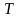раз.
Тогда уравнение (1.44) примет вид:
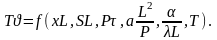(1.44/)
Полагая, что
,
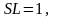
получим:
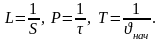
Подставляя значения
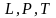в уравнение (1.44/)
будем иметь:
или
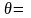
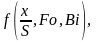(1.45)
где
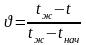- относительная температура;
-
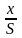относительная
длина;
-
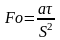критерий Фурье;
-
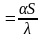критерий Био.
Критерий Био
характеризует массивность тел и
определяет отношение внутреннего
теплового сопротивления тела
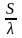к внешнему сопротивлению теплоотдачи
,
т.е.
=
.
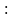Уравнение (1.45) справедливо для случая нагревания или охлаждения не только пластины, но и цилиндра, и шара при граничных условиях третьего рода. При нагревании тел постоянным тепловым потоком (граничные условия второго рода) критериальное уравнение (1.45) примет вид:
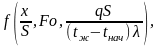(1.46)
и при граничных условиях первого рода
(1.47)