1.1.6. Условие однозначности решения

Полученное дифференциальное уравнение Фурье описывает явление передачи теплоты теплопроводностью в самом общем виде. Для того, чтобы применить его к конкретному случаю, необходимо знать распределение температур в теле в начальный момент времени, или начальные условия. Кроме того, должны быть известны: геометрическая форма и размеры тела, физические параметры среды и тела и граничные условия, характеризующие распределение температур на поверхности тела, или взаимодействие изуча-емого тела с окружающей средой. Все эти частные особенности совместно с дифференциальным уравнением дают полное математическое описание кон-кретного процесса теплопроводности и называются условиями одноз-начности, или краевыми условиями.

Начальные условия необходимы при рассмотрении нестационарных процессов и состоят в задании закона распределения температуры внутри тела в начальный момент времени. В общем случае начальное условие аналитически может быть записано следующим образом:

при 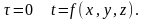(1.16)

На практике часто встречаются задачи с простым начальным условием

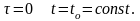(1.17)

Таковы, в частности, начальные условия вывода системы из устано-вившегося режима (разогрев из «холодного» состояния, охлаждения после работы при стационарном режиме и т. д.). В этом случае решение уравнения значительно упрощается.

Возможны предельные случаи, когда можно пренебречь точным учетом начальных условий. В качестве примера рассмотрим распрост-ранение теплоты в стержне. Если расчетный момент времени достаточно удален от начального, температурное поле определяется практически только граничными условиями: влияние начальных условий ослабевает с течением времени. Таким образом, можно полагать, что опыт длится бесконечно долго и начальные условия отпадают. К такому же случаю сводится задача о периодическом колебании температур на границе: по истечении большого промежутка времени температура точек системы меняется по перио-дическому закону с частотой, совпадающей с частотой колебания температуры на границе. При точном учете начального распределения периодического колебания не возникает, однако с нужной для практики точностью влиянием этой ошибки можно пренебречь.

Для тел произвольной формы начальные условия оказывают влияние лишь на первой стадии нестационарного процесса: начиная с некоторого мо-мента наступает режим, называемый регулярным, при котором распределе-ние температур в теле определяется только граничными условиями и не за-висит от начальных.

Граничные условия могут быть заданы несколькими способами.

Граничные условия первого рода. Задается распределение температу-ры на поверхности тела для каждого момента времени:

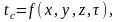(1.18)

где - температура на поверхности тела; 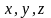- координаты поверхности тела.

В частном случае, когда температура на поверхности является посто-янной на протяжении всего времени протекания процесса теплообмена, уравнение (1.18) упрощается и принимает вид:

= .

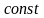К граничным условиям первого рода могут быть сведены задачи разогрева и охлаждения системы при заданном изменении температуры на границе или весьма интенсивном теплообмене на поверхности (температура стенок близка к температуре среды). Однако круг таких практических задач ограничен и относительно простые граничные условия первого рода исполь-зуются в основном при разработке математических методов и оценочных расчетов.

Граничные условия второго рода. Задаются величины плотности теплового потока для каждой точки поверхности тела и любого момента времени.

Аналитически это можно представить в виде:

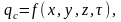(1.19)

где - плотность теплового потока на поверхности тела.

В простейшем случае плотность теплового потока на поверхности и во времени остается постоянной:

= .

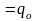К граничным условиям второго рода относятся часто встречающиеся на практике задачи нагрева системы внешним источником – нагревателем, причем собственная температура последнего, свойства поверхности, а также температура и свойства поверхности нагреваемого объекта могут меняться во времени. Кроме того, из-за взаимного переизлучения температура нагре-вателя (а следовательно, и тепловой поток) становятся зависимыми от температуры объекта, что затрудняет расчет падающего на исследуемую сис-тему теплового потока.

К частному случаю граничных условий второго рода – отсутствию потока на поверхности (тепловой изоляции) сводится так называемая симметричная задача, когда система, представляющая собой тело с геомет-рической симметрией, обогревается по всей поверхности равномерно (нагрев пластины в среде с постоянной температурой).

Граничные условия третьего рода. Задаются температура окружаю-щей среды и закон теплообмена между поверхностью тела и окружающей средой. Для описания процесса теплообмена между поверхностью тела и средой используется закон Ньютона-Рихмана. Согласно этому закону коли-чество теплоты, отводимое единицей поверхности тела в единицу времени, пропорционально разности температур поверхности тела и окружающей среды ( > ):

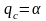( - ), (1.20)

где - коэффициент пропорциональности, называемый коэффициентом теплоотдачи, Вт/(м^{2 о}С).

Коэффициент теплоотдачи характеризует интенсивность теплообмена между поверхностью тела и окружающей средой. Численно он равен коли-честву теплоты, отдаваемой (или воспринимаемой) единицей поверхности в единицу времени при разности температур между поверхностью тела и окружающей средой в 1 ^оС.

Согласно закону сохранения энергии количество теплоты, которое отводится с единицы поверхности в единицу времени вследствие тепло-отдачи (1.20), должно равняться количеству теплоты, подводимому к еди-нице поверхности в единицу времени вследствие теплопроводности из внутренних объемов тела (1.8), т.е.

( - )= ,

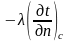где 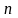- нормаль к поверхности тела, а индекс «с» указывает на то, что температура и температурный градиент относятся к поверхности тела при .

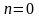Окончательно граничные условия третьего рода можно записать в виде:

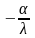= ( - ). (1.21)

Уравнение (1.21) является по существу частным выражением закона сохранения энергии для поверхности тела. Коэффициент теплоотдачи в этом уравнении в отличие от коэффициента теплопроводности не является физической постоянной, характерной для того или иного вещества. В общем случае он отражает совместное действие конвекции и излучения и поэтому зависит от множества факторов. Достаточно отметить, что одна только конвективная часть определяется геометрической формой и размерами тела, физическими свойствами омывающей его среды, направлением и скоростью омывания, температурными условиями и другими характе-ристиками явления, поэтому вся сложность вопроса о теплообмене между телом и окружающей средой сосредоточивается на методике определения величины при конкретных условиях задачи.

Граничные условия третьего рода широко применяются на практике (например, конвективный теплообмен на границе), поэтому многие решения приводятся в руководствах в виде таблиц и графиков.

Граничные условия четвертого рода. Задаются условия тепло-обмена системы тел или тела с окружающей средой по закону тепло-проводности. Предполагается, что между телами осуществляется идеальный контакт (температуры соприкасающихся поверхностей одинаковы).

При этом имеет место равенство тепловых потоков, проходящих через поверхность соприкосновения, т.е.

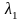
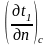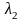
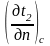= . (1.22)

В задачах с граничными условиями четвертого рода задается отно-шение тангенсов угла наклона касательных к температурным кривым в точке соприкосновения тел или тела и среды (рис.1.4)

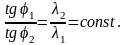(1.23)

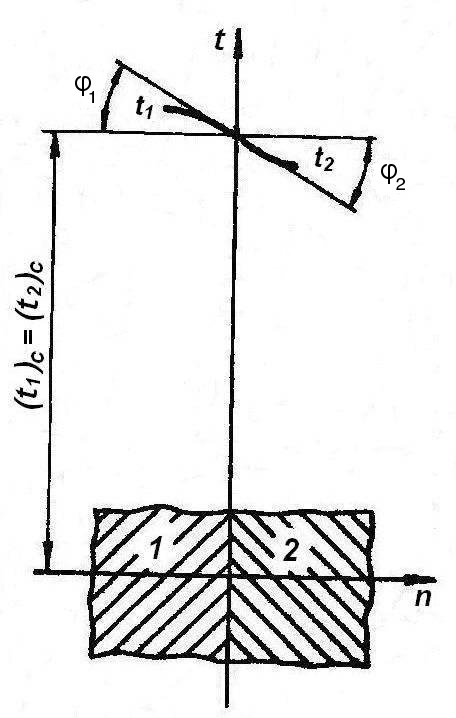
Рис.1.4.К граничным условиям четвертого рода

Граничные условия четвертого рода по существу дают правило сопря-жения температурных полей объекта исследования и внешнего тела, в котором теплота передается путем теплопроводности. Для однозначной формулировки задачи в этом случае, естественно, необходимы дополни-тельные сведения о протекании процесса во внешнем теле.

В связи с развитием высокотемпературной теплофизики задачи с граничными условиями четвертого рода приобрели первостепенное зна-чение для расчета многослойных покрытий головок ракет, элементов прео-бразователей энергии и т.д.