1.1.3. Тепловой поток. Закон Фурье
Теплота самопроизвольно
переносится только в сторону убывания
температуры. Количество теплоты,
переносимой через какую – либо
поверх-ность в единицу времени, называется
тепловым потоком
[Bт].
Тепловой поток, отнесенный к единице
поверхности, называется плотностью
теплового потока, или удельным тепловым
потоком, или тепловой нагрузкой
поверхности нагрева, т.е.
(1.7)
Если тепловой
поток отнесен к единице изотермической
поверхности, то величина
является вектором, направление которого
совпадает с направлением распространения
теплоты в данной точке и противоположно
направлению вектора температурного
градиента (рис.1.2).
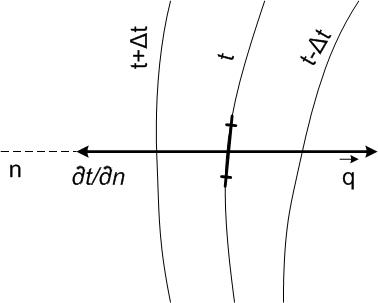
Рис.1.2.К выводу закона Фурье
Изучая процесс теплопроводности в твердых телах, Фурье экспе-риментально установил, что количество переданной теплоты пропорци-онально падению температуры, времени и площади сечения, перпен-дикулярного направлению распространения теплоты. Если количество пере-данной теплоты отнести к единице сечения и единице времени, то уста-новленную зависимость можно записать в виде:
=
.
(1.8)
Уравнение (1.8) является математическим выражением основного закона теплопроводности – закона Фурье. Этот закон лежит в основе всех теоретических и экспериментальных исследований процессов теплопро-водности.
1.1.4.Коэффициент теплопроводности
Коэффициент
пропорциональности
в уравнении (1.8) является физическим
параметром вещества, характеризующим
способность тел проводить теплоту, и
называемый коэффициентом теплопроводности.
Его размерность Вт/(м оС).
Величина коэффициента теплопроводности представляет собой коли-чество теплоты, которое проходит в единицу времени через один квад-ратный метр изотермической поверхности при температурном градиенте, равном единице. На величину коэффициента влияет много факторов: тем-пература, давление, структура, влажность, агрегатное состояние тела, меха-низм переноса теплоты и т.д. Это сильно затрудняет выбор правильного значения коэффициента теплопроводности, поэтому при ответственных расчетах следует определять его путем специального изучения применя-емого материала. В технических же расчетах значения коэффициента теплопроводности обычно устанавливают по справочным таблицам. При этом надо следить за тем, чтобы физические характеристики материала (структура, плотность, влажность, температура, давление) соответствовали выбранным условиям. Так как при распределении теплоты температура в различных частях тела неодинакова, то в первую очередь важно знать зависимость коэффициента теплопроводности от температуры. Для боль-шого числа материалов эта зависимость оказывается почти линейной, т.е.
=
где
- коэффициент
теплопроводности при температуре
,
Вт/(м оС);
-
температура, оС;
-
температурный коэффициент, определяемый
опытным путем.
Лучшими проводниками теплоты являются металлы, у которых изменяется от 3 до 458 Вт/(м оС). Коэффициенты теплопроводности чистых металлов, за исключением алюминия, с возрастанием температуры убывают. Теплоту в металлах переносят главным образом свободные электроны. Са-мым теплопроводным металлом является чистое серебро ( =458Вт/(м оС)). Уменьшение чистых металлов с ростом температуры объясняют усиле-нием тепловых неоднородностей, приводящих к рассеиванию электронов. При наличии разного рода примесей металлов резко убывает, что связано с увеличением структурных неоднородностей, которые также приводят к рассеиванию электронов.
Коэффициенты теплопроводности теплоизоляционных и строительных материалов, имеющих пористую структуру, при повышении температуры возрастают по линейному закону и изменяются в пределах от 0,02 до 3,0 Вт/(м оС). Значительное влияние на коэффициенты теплопроводности пористых материалов оказывают газы, заполняющие поры и обладающие весьма малыми коэффициентами теплопроводности по сравнению с твердых компонентов. Увеличение пористых материалов при повышении температуры объясняется значительным возрастанием лучистого тепло-обмена между поверхностями твердого «скелета» пор через разделяющие их воздушные ячейки. Роль конвекции в росте повышается с увеличением размеров воздушных включений в материал, поэтому эффективный коэф-фициент теплопроводности пористых тел имеет сложную природу и является условной величиной. Эта условная величина имеет смысл коэффициента теплопроводности некоторого однородного тела, через которое при одина-ковой форме, размерах и температуре на границах проходит то же коли-чество теплоты, что и через данное пористое тело.
Большое влияние на оказывает влажность вещества. Опыты показы-вают, что с увеличением влажности материала коэффициент теплопро-водности значительно возрастает. Этот эффект может быть объяснен конвек-тивным переносом теплоты, возникающим благодаря капиллярному движе-нию воды внутри пористого материала, и частично тем, что абсорбционно связанная влага имеет другие характеристики по сравнению со свободной водой. Кроме того, чем выше объемная плотность материала, тем меньше он имеет пор и тем выше его коэффициент теплопроводности.
Жидкости занимают промежуточное положение между газами и твер-дыми телами. Поэтому теплота переносится в них как за счет колебаний молекул путем обмена энергии при соударениях, так и диффундирующими молекулами. Коэффициенты теплопроводности большинства капельных жидкостей с повышением температуры убывают. Их значения находятся в пределах от 0,08 до 0,65 Вт/(моС). Вода является исключением. С уве-личением температуры от 0 до 127 оС ее коэффициент теплопроводности повышается, а при дальнейшем возрастании температуры уменьшается. От давления капельных жидкостей практически не зависит.
Теплопроводность в газах осуществляется за счет диффузии молекул. Так как с ростом температуры диффузия возрастает, то буде увеличиваться и коэффициент теплопроводности. От давления практически не зависит. Для газов изменяется в пределах от 0,006 до 0,6 Вт/(м оС).
Числовые значения коэффициентов теплопроводности различных мате-риалов, включая и остальные теплофизические характеристики, приведены в соответствующей литературе.