2.5.3. Конвективный теплообмен при вынужденном внешнем обтекании тел

В ряде случаев, например, в рекуператорах, трубы омываются внешним потоком газов. В результате теплообмена с внешней греющей средой стенки труб нагреваются и передают теплоту газовому потоку, протекающему внутри труб.

В низкотемпературных печах часто для интенсификации конвек-тивного теплообмена организуют искусственную циркуляцию газовой сре-ды. Следовательно, этот вид конвективного теплообмена в технике встре-чается довольно часто.

Прежде чем привести расчетные зависимости, рассмотрим факторы, влияющие на теплоотдачу. Вначале рассмотрим наиболее простой случай обтекания длинного цилиндра поперечным потоком теплоносителя. При поперечном обтекании какого-либо тела, например цилиндра, на передней (фронтальной) части возникает пограничный слой, толщина которого увеличивается в направлении движения потока. При обтекании цилиндра скорость достигает максимальной величины в точке периметра, отвечающей углу (угол отсчитывается от лобовой точки), и примерно в этом же месте начинается разрушение пограничного слоя, который как бы изолирует эту часть поверхности цилиндра от остальной массы потока. За задней (кормовой) частью цилиндра образуется зона с сильно развитой турбулентностью (рис.2.10). Через пограничный слой теплота передается только теплопроводностью. Поэтому с ростом толщины слоя уменьшается количество передаваемой теплоты, что равносильно уменьшению величины коэффициента теплоотдачи, минимальное значение которой будет в точке, где значение толщины пограничного слоя максимально. Повышенное значение коэффициента теплоотдачи в лобовой части объясняется малой толщиной пограничного слоя. Усиление турбулентных перемещений в кормовой части приводит к увеличению коэффициента теплоотдачи.

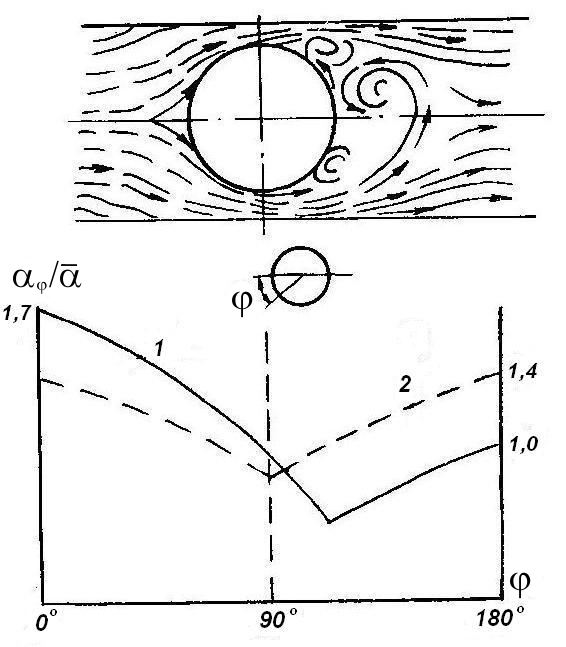
Рис.2.10 Изменение отношения локального значения коэффициента

теплоотдачи по поверхности к его среднему значению для

всей поверхности при обтекании цилиндра внешним пото-

ком: 1 -

Проанализировав и обобщив существующие экспериментальные дан-ные для расчета среднего по периметру трубы коэффициента теплоотдачи, можно рекомендовать зависимость: при

( / ) ; (2.37)

при

( / ) . (2.38)

Формулы (2.37) и (2.38) справедливы для любых жидкостей. В этих выражениях значения теплофизических свойств потока принимаются по его температуре. В качестве определяющего размера в критерии Нуссельта и Рейнольдса подставляется диаметр трубы

Соотношения (2.37) и (2.38) справедливы лишь тогда, когда угол , составленный направлением движения потока и осью трубы, равен 90^о. За-висимость теплоотдачи от величины угла атаки представлена на рис.2.11.

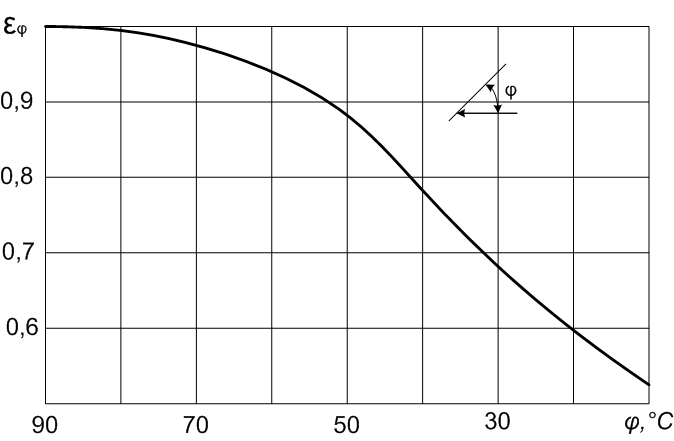
Рис.2.11 Поправочный коэффициент на угол атаки

Здесь по оси абсцисс отложено значение , а по оси ординат – значение , которое представляет собой отношение теплоотдачи при угле атаки к теплоотдаче при =90^о, т.е. = . Как видно из рис.2.11, с уменьшением угла атаки значение падает. При этом расчетная формула для коэффициента теплоотдачи принимает вид:

. (2.39)

Опыты, проведенные по определению коэффициента теплоотдачи от воздуха к телам самой различной формы, позволили создать обобщенное расчетное уравнение:

(2.40)

Теплофизические свойства воздуха в этом уравнении выбираются по его температуре. За определяющий размер принимается отношение перимет-ра сечения к

Уравнения (2.37), (2.38) и (2.40) не учитывают влияния свободной конвекции. С учетом последней уравнение теплоотдачи принимает вид:

(2.41)

В уравнении (2.41) учитывает передачу теплоты теплопро-водностью. Можно принять, что для цилиндра , для шара , для плиты . Величина представляет собой суммарный критерий Рейнольдса, т.е.

= .

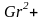
За определяющую температуру в этом уравнении принимается полусумма температур потока и твердой поверхности.

При рассмотрении уравнений (2.37), (2.38), (2.40) и (2.41) можно сделать вывод о том, что на величину коэффициента теплоотдачи влияют размеры тела, теплофизические свойства и скорость потока.

После рассмотрения факторов, влияющих на теплоотдачу одиночного цилиндра, можно перейти к вопросам, связанным с теплоотдачей пучков труб. Известно два основных способа расположения труб в пучках: коридорное и шахматное. От способа расположения труб в пучке зависит характер их обтекания потоком, а следовательно, и величина коэффициента теплоотдачи. Шахматное расположение труб позволяет получить больший коэффициент теплопередачи, чем коридорное. Но при коридорном распо-ложении трубы меньше заносятся пылью, содержащейся в дымовых газах.

Характер движения потоков и изменение локального значения коэффициента теплоотдачи на поверхности труб в пучках показаны на рис. 2.12.

Каждый из пучков харктеризуется внешним диаметром труб , поперечным шагом , продольным шагом и числом рядов труб по ходу движения жидкости . В этом и другом случае трубы первого ряда находятся в условиях, мало отличающихся от одиночной трубы. В после-дующих рядах коэффициент теплоотдачи увеличивается вследствие допол-нительной турбулизации потока при его прохождении через предыдущие ряды труб. Однако при увеличении рядов труб по ходу потока до 20 и более, увеличения коэффициента теплоотдачи не наблюдается.

По изучению теплоотдачи в зависимости от типа пучка, пучка диаметра труб, расстояния между ними, температуры жидкости и других факторов проведено довольно большое количество исследований. Теплоотдача перво-го ряда различна и определяется начальной турбулентностью потока. Тепло-отдача второго и третьего рядов по сравнению с первым постепенно воз-растает. Если теплоотдачу третьего ряда принять за 100%, то в шахматных и коридорных пучках теплоотдача первого ряда составит всего лишь около 60%, второго ряда в коридорных пучках – около 90%, и в шахматных – около 70%. Причиной возрастания теплоотдачи, как уже отмечалось, является увеличение турбулентности потока при прохождении его через пучок. Начиная с третьего ряда, турбулентность потока принимает ста-бильный характер, присущий данной компоновке пучка. По абсолютному

значению теплоотдача в шахматных пучках выше, чем в коридорных, что обуславливается лучшим перемешиванием жидкости, омывающей трубы.

На основе анализа и обобщения опытных данных, для расчета средних значений коэффициентов теплоотдачи третьего и последующих рядов труб пучка при обычно используют следующие уравнения:

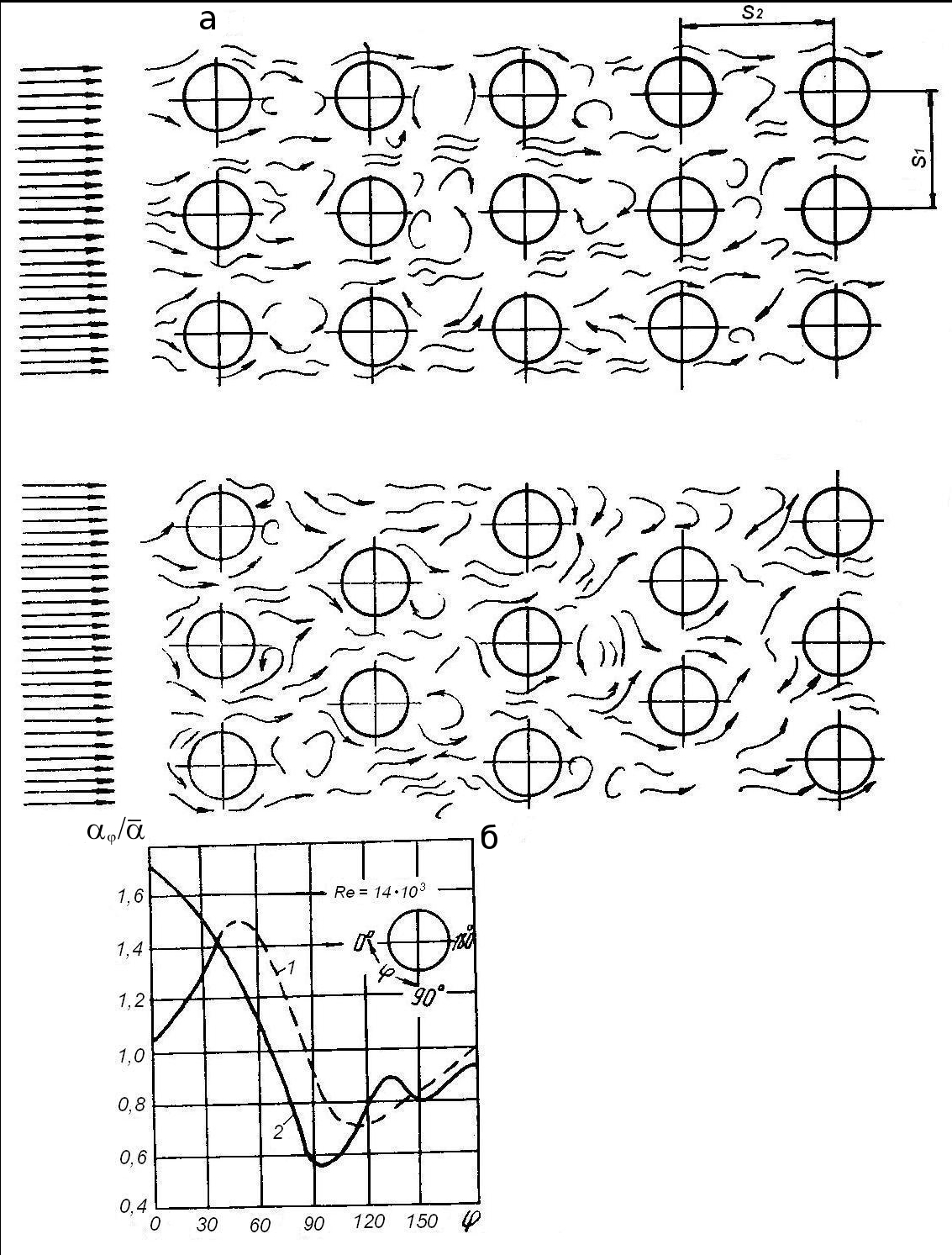
Рис.2.12 Схема движения потоков (а) и изменение локального коэффициента

теплоотдачи по поверхности труб в пучках (б):

1 – в коридорных; 2 - в шахматных

при координатном расположении труб в пучке

(2.42)

где - поправочный коэффициент, учитывающий влияние отно-сительных шагов для глубинных рядов;

при шахматном расположении труб в пучке

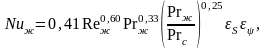(2.43)

где при = ( ) , а при =1,12.

В этих формулах в качестве определяющих температуры, скорости, размера приняты: средняя температура потока; скорость в самом узком сечении ряда; диаметр трубки.

Значения коэффициента теплоотдачи для трубок первого ряда пучка определяются путем умножения найденного значения для трубок третьего ряда на поправочный коэффициент =0,60. Для трубок второго ряда в коридорных пучках =0,90, а в шахматных пучках =0,70.

Если же требуется определить средний коэффициент теплоотдачи пучка в целом, то в этом случае необходимо усреднение найденных зна-чений , которое производится следующим образом:

(2.44)

где 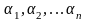- коэффициент теплоотдачи для отдельных рядов; - поверхности нагрева всех трубок в ряду.

Его можно также определить по формуле

(2.45)

где - количество рядов труб по ходу потока жидкости.

При омывании пучка потоком газов, движущихся под углом к оси труб , коэффициент теплоотдачи уменьшается по сравнению с поперечным обтеканием. В этом случае среднее значение коэффициента теплоотдачи следует умножить на поправочный коэффициент , величина которого выбирается в зависимости от величины угла атаки

……..90 80 70 60 50 40 30 20 10

…….1,0 1,0 0,98 0,94 0,88 0,78 0,67 0,52 0,42

Скорость потока и определяющий размер выбираются, как и при поперечном обтекании.