2.5.2. Расчетные зависимости для определения коэффициентов теплоотдачи при вынужденном движении теплоносителя в каналах круглого сечения

При ламинарном течении любой жидкости (Re<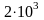 ) для определения среднего коэффициента теплоотдачи рекомендуется следующая расчетная формула:

(2.30)

Здесь теплоотдача существенно зависит от интенсивности свободной конвекции, которая определяется значением критерия Грасгофа

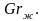
Значение поправочного коэффициента зависит от отношения длины канала к его диаметру 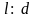и может быть определено с помощью табл. 2.4. Из таблицы видно, что стабилизация потока наступает на расстоянии 50 диаметров трубы от входного сечения. За определяющую температуру в формуле (2.30) принята средняя температура потока, за определяющую скорость – средняя скорость потока, а за определяющий размер – экви-валентный диаметр канала. Сомножитель (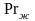 / ) учитывает направление теплового потока, причем вычисляется по температуре потока, а - по температуре стенки.

Таблица 2.4

Зависимость поправочного коэффициента от ( )

Значение критерия Re	Отношение
	1	2	5	10	15	20	30	40	50
	1,90	1,70	1,44	1,28	1,18	1,13	1,05	1,03	1
	1,51	1,40	1,27	1,18	1,13	1,10	1,04	1,02	1
	1,28	1,22	1,15	1,10	1,08	1,06	1,03	1,02	1
	1,14	1,11	1,08	1,05	1,04	1,03	1,02	1,01	1

При развитом турбулентном режиме расчетная формула для среднего коэффициента теплоотдачи имеет следующий вид:

(2.31)

За определяющую температуру здесь принята средняя температура газа (жидкости), а за определяющий размер – эквивалентный диаметр .

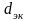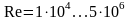Соотношение (2.31) применимо к трубам любой формы поперечного сечения: круглого, квадратного, прямоугольного кольцевого ( ) и др. и для всех упругих и капельных жидкостей при и

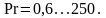
Оно справедливо и для каналов сложного поперечного сечения, когда в трубе большого диаметра расположена одна или несколько труб меньшего диаметра (продольное омывание).

Множитель ( / ) представляет собой поправку, учитывающую зависимость физических свойств теплоносителя (в основном вязкости) от температуры. В зависимости от направления теплового потока эта поправка может быть как больше, так и меньше единицы.

Из анализа (2.31) следует, что при турбулентном режиме течения коэффициент теплоотдачи в наибольшей степени зависит от скорости движения теплоносителя и его плотности пропорционально ( ) . Далее теплоотдача зависит от физических свойств среды и изменяется пропорционально 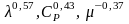где - коэффициент теплопроводности теп-лоносителя; 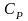- его теплоемкость; - коэффициент динамической вязкости.

Влияние геометрического размера канала на теплоотдачу определяется зависимостью ~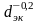 , т.е. это влияние оказывается относительно слабым.

Для воздуха (или двухатомных газов) соотношение (2.31) упрощается ( и / 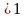) и принимает вид:

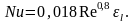(2.31,а)

В ряде случаев можно с небольшой погрешностью воспользоваться более простой формулой:

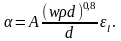(2.32,а)

Коэффициент зависит от температуры и выбирается по табл. 2.5.

Таблица 2.5

Значение коэффициента в зависимости от температуры

Температура среды, оС	Воздух		Дымовые газы
	(нагрев)	(охлаждение)	(нагрев)	(охлаждение)
0	2,86	3,74	2,89	3,76
400	3,48	4,55	3,92	5,16
800	3,98	5,19	4,67	6,14
1200	4,31	5,65	5,19	6,88

Все вышеперечисленные формулы не учитывают местных сопро-тивлений, шероховатости каналов и условий входа потока в канал. Известно, что повышение шероховатости приводит к увеличению коэффициента теп-лоотдачи только при турбулентном режиме движения. Влияние шерохо-ватости на теплообмен усиливается при увеличении величины критерия Рейнольдса.

Теплоотдача в прямых трубах при переходном режиме движения изучена слабо. Поэтому расчетные зависимости здесь не приведены. Опы-тами также установлено, что в изогнутых трубах при прочих равных условиях значение коэффициента теплоотдачи выше, чем в прямых трубах вследствие дополнительной турбулизации потока, вызываемой центро-бежными силами. Поэтому теплоотдача в змеевиках выше, чем в прямых трубах, несмотря на то, что переход ламинарного режима движения в турбулентный затягивается до значений величины критерия Рейнольдса 20000…30000. Величина критического числа Рейнольдса зависит от относительной кривизны канала, под которой понимается отношение внут-реннего диаметра трубы к радиусу закругления 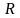, т.е. . Для змеевиков при

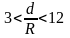
= (2.33)

При расчете теплоотдачи змеевиковых труб при 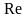можно воспользоваться вышеприведенными формулами для прямых труб с вве-дением поправочного коэффициента , величина которого определяется кривизной трубы и может быть определена по формуле:

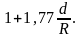= (2.34)

Несколько иначе выглядят расчетные формулы конвективного теплообмена при малых значениях критерия Прандтля (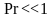 ). Этот случай хараткерен для теплоотдачи жидкого металла. Для жидких металлов коэффициент температуропроводности значительно превышает коэффици-ент кинематической вязкости. В этом случае толщина теплового погра-ничного слоя значительно больше толщины гидродинамического погранич-ного слоя. Вследствие этого процесс молекулярного переноса теплоты теп-лопроводностью имеет большое значение не только в пограничном слое, но и в ядре турбулентного потока.

Расчет средней теплоотдачи в жидких металлах может быть произведен по формуле:

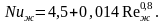(2.35)

Формула (2.35) проверена для турбулентного режима движения потока и круглых прямых труб при 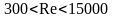. Теплофизические свойства металла выбираются по его среднеарифметической температуре.

Если отношени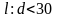е , то вычисленное значение коэффициента теплоотдачи умножается на поправочный коэффициент , величина которого определяется по формуле:

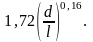= (2.36)