2.4.3.Теплообмен свободной конвекцией в ограниченном объеме
В ограниченном объеме теплообмен свободной конвекцией между поверхностью твердого тела и средой имеет некоторые особенности. Прежде всего, характер перемещения среды зависит от величины, формы и распо-ложения не только нагретых, но и холодных поверхностей. На рис. 2.5 показан характер движения газов между двумя парами горизонтальных плоскостей и коаксиальными цилиндрами. Из рисунка видно, что для одной и той же системы тел, в зависимости от расположения нагретой поверхности, меняется и характер движения среды. Количество теплоты, переносимое от горячей поверхности к холодной через вертикальный слой жидкости, иногда увеличивается, если пространство между вертикальными стенками разделено тонкими горизонтальными перегородками на меньшие объемы.
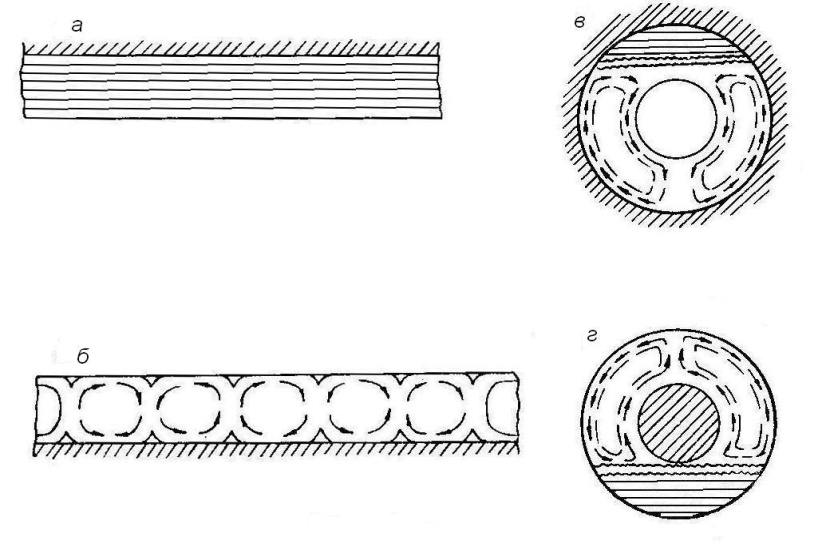
Рис.2.5 Свободное движение газа в ограниченном объеме. Горизонтальные
прослойки: а – с нагретой верхней поверхностью; б – с нижней
нагретой поверхностью; в – цилиндрические горизонтальные
прослойки с нагретой внешней поверхностью; г – с внутренней
горизонтальной поверхностью
Характер изменения
толщины пограничных слоев, а также
темпе-ратуры среды между холодной и
горячей вертикальными стенками показан
на рис. 2.6. На нагретой поверхности
толщина пограничного слоя увели-чивается
в направлении снизу вверх, а на холодной
– сверху вниз. Темпера-тура среды резко
меняется по толщине пограничного слоя.
В пространстве между пограничными
слоями температура среды почти не
изменяется. Из рис. 2.6 видно, что в условиях
ограниченного объема передача теплоты
в значительной степени осуществляется
теплопроводностью через погранич-ный
слой. Поэтому расчет теплообмена
свободной конвекцией в ограни-ченном
объеме проводится по формулам, полученным
для расчетов передачи теплоты
теплопроводностью посредством введения
в эти формулы экви-валентного коэффициента
теплопроводности
.
Если значение последнего разделить на
среды, то получим безразмерную величину
=
/
,
которая характеризует собой влияние
конвекции и называется коэффициентом
кон-векции.
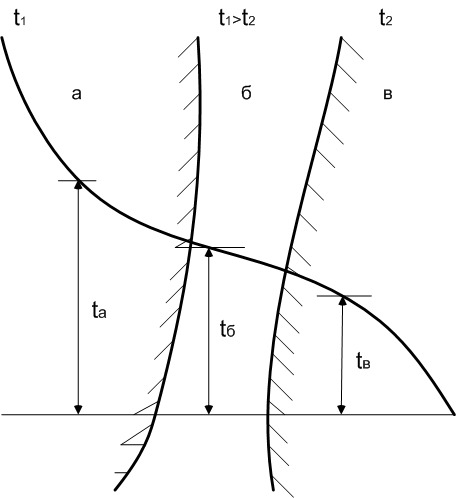
Рис.2.6 Изменение толщины пограничных слоев и температуры
среды в ограниченном объеме:
а – пограничный слой на горячей стенке; б – центральное ядро; в –
пограничный слой на холодной стенке
Так
как циркуляция жидкости обусловлена
разностью плоскостей на-гретых и холодных
частиц и определяется критерием
,
то
должно быть функцией того же аргумента,
т.е.
.
При вычислении критериев подобия независимо от формы прослойки за определяющий размер принята ее толщина , а за определяющую температуру – средняя температура жидкости
0,5(
).
При
малых значениях аргумента
<1000
значение функции
=1.
Это означает, что при малых значениях
теплоотдача от горячей стенки к холодной
в прослойках обуславливается только
теплопроводностью жидкости.
При
значeнии
=0,105(
)
(2.26)
и
при
=0,40(
)
. (2.27)
Снижение
интенсивности теплопередачи при больших
значениях аргу-мента объясняется
взаимной помехой в движении поднимающихся
(нагре-тых) и опускающихся (охлажденных)
струек жидкости. В приближенных расчетах
вместо (2.26) и (2.27) для всей области
значений аргументов
можно применять зависимость
=0,18(
)
,
(2.28)
которую можно привести к виду
=
(2.29)
где
