2.2. Математическое описание конвективного теплообмена

Конвективный теплообмен определяется совокупностью тепловых и гидродинамических процессов и описывается системой дифференциальных уравнений. Рассмотрим эти уравнения.

Уравнение теплоотдачи. У поверхности теплообмена теплопередача осуществляется в тонком слое жидкости теплопроводностью, поэтому для слоя можно использовать закон Фурье:

, (2.4)

где - нормаль к поверхности тела.

С другой стороны, согласно закону Ньютона-Рихмана имеем:

( - ), (2.5)

где - температура стенки, - температура невозмущенного потока.

Приравнивая правые части уравнений (2.4) и (2.5), получаем:

, (2.6)

где = - и = - .

При изменении температуры только в направлении одной координаты , нормальной к поверхности тела, уравнение (2.6) можно записать в следующем виде:

. (2.6, а)

Уравнение энергии. В уравнение (2.6, а) входит температурный градиент. Чтобы его найти, нужно вычислить поле температуры, которое описывается дифференциальным уравнением. Это уравнение легко получить, если рассмотреть закон сохранения энергии для элементарного объема среды 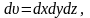изменение теплосодержания которого в единицу времени сос-тавит:

(2.7) где с – удельная теплоемкость, плотность жидкости; - полная (субстанциальная) производная температуры по времени.

С другой стороны, изменение теплосодержания определяется разнос-тью количеств теплоты, внесенной и вынесенной в этот объем по направлениям всех трех осей, т.е.

(2.8)

В соответствии с законом Фурье:

(2.9)

Приравнивая правые части уравнений (2.7) и (2.8) и используя уравнение (2.9), получим в предположении постоянства теплопро-проводности:

= (2.10)

Учитывая, что температура является функцией времени и координат, можно написать:

= (2.11)

так как изменение соответствующей координаты в единицу времени есть составляющая скорости по данной координате. Окончательно уравнение (2.10) принимает вид:

= (2.12)

Уравнение (2.12) называют уравнением Фурье-Кирхгофа.

Из уравнения (2.12) видно, что температурное поле в движущейся жидкости зависит от составляющих скорости и . Следовательно, для их определения надо использовать уравнения, которые бы описывали изме-нение скорости во времени и пространстве. Такими уравнениями являются дифференциальные уравнения движения.

Уравнения движения. Вывод дифференциального уравнения движения вязкой жидкости требует громоздких выкладок и приводится в соответ-ствующей литературе. Этот вывод основан на втором законе Ньютона: сила равна массе, умноженной на ускорение.

Приведем уравнение движения без вывода в проекции только на ось :

где - проекция ускорения силы тяжести на ось ; - давление жидкости; - коэффициент динамической вязкости жидкости.

Уравнение написано без учета зависимости физических свойств жид-кости от температуры.

Аналогично уравнению (2.13) можно написать проекции уравнения движения на оси и . Это - уравнение Навье – Стокса.

Поскольку в уравнение движения входит неизвестная величина , то необходимо еще одно уравнение. Таким уравнением является уравнение сплошности.

Уравнение сплошности (неразрывности). Это уравнение является математическим выражением закона сохранения массы.

Для сжимаемой жидкости оно имеет вид:

(2.14)

Для несжимаемой жидкости ( ) получаем:

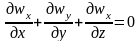, (2.15)

или, что то же самое

. (2.16)

Введем для сокращения обозначение

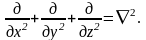
Тогда процесс конвективного теплообмена однородной среде описывается следующей системой дифференциальных уравнений:

; (2.6,б)

(2.10,а)

(2.13,а)

. (2.16,а)

Система дифференциальных уравнений (2.6,а), (2.10,а), (2.13,а) и (2.16) позволяет получить бесчисленное количество решений. Для того, чтобы получить единственное решение, необходимо к системе дифференциальных уравнений присоединить условия однозначности, которые конкретизируют задачу и позволяют получать единственные решения. Условия однознач-ности конвективного теплообмена состоят из: 1) геометрических условий, характеризующих форму и размеры тела или системы, в которой протекает процесс; 2) физических условий, характеризующих физические свойства среды; 3)временных или начальных условий, характеризующих особенности процесса в начальный момент времени; для стационарных задач эти условия отпадают; 4) граничных условий, характеризующих особенности протекания процесса на границах жидкой среды.

В последних должны быть заданы граничные значения зависимых (искомых) переменных или их производных. Например, для любого момента времени задаются распределение температур или тепловых потоков и ско-ростей по поверхности тела, распределение температур и скоростей жид-костей на входе в канал или на большом удалении от рассматриваемой по-верхности.