2. Конвекция

2.1.Общие сведения о конвективном теплообмене

Под конвекцией теплоты понимают процесс переноса тепловой энер-гии при перемещении объемов жидкости или газа в пространстве из области с одной температурой в область с другой. Конвекция возможна только в текучей среде и неразрывно связана с переносом самой среды. Удельные по-токи конвективного переноса теплоты могут быть весьма различными ( от 10 до 10⁸Вт/м²).

Конвекция теплоты всегда сопровождается теплопроводностью, так как при движении жидкости или газа неизбежно соприкосновение отдель-ных частиц, имеющих различные температуры. Совместный процесс конвек-ции и теплопроводности называют конвективным теплообменом. При инже-нерных расчетах обычно определяют конвективный теплообмен между по-током жидкости или газа и поверхностью твердого тела. Этот процесс конвективного теплообмена называют конвективной теплоотдачей. Кон-вективная теплоотдача часто сопровождается теплоотдачей излучением.

Конвекция всегда связана с движением теплопередающего или тепло-воспринимающего вещества. Движение жидкости или газа при этом может быть вызвано либо внешними силами, например, напором, создаваемым вентилятором, компрессором или насосом, либо наличием подъемной силы, возникающей вследствие разности плотностей нагретых и холодных частиц.

Теплообмен между поверхностью твердого тела и движущимся потоком при воздействии на поток внешних сил называется вынужденной конвекцией.

Теплообмен между поверхностью твердого тела и жидкостью или газом, которые перемещаются под влиянием разности плотностей нагретых и холодных частиц, называется свободной или естественной конвекцией. В ряде случаев одновременно с вынужденным движением может быть естест-венное (свободное) движение. Влияние последнего будет тем больше, чем меньше скорость вынужденного движения. Конвективный теплообмен по-мимо причин перемещения теплоносителя (свободное или вынужденное движение) подразделяется также и по режимам движения потоков (лами-нарный и турбулентный).

Перенос теплоты в направлении, перпендикулярном направлению движения потока теплоносителя при ламинарном режиме определяется только процессом молекулярного переноса вещества, который в свою оче-редь зависит от величины коэффициента теплопроводности жидкости или газа. При турбулентном режиме перенос теплоты обусловлен поперечным перемещением микро- и макрообъемов вещества (вихрей). Чем выше скорость движения потока, тем больше при прочих равных условиях интен-сивность поперечного перемещения теплоносителя. В этом случае моле-кулярный перенос теплоты внутри потока имеет второстепенное значение.

Установлено, что в потоке вязкой жидкости, омывающем какое-либо тело, по мере приближения к его поверхности скорость уменьшается и на самой поверхности становится равной нулю. Вывод о том, что скорость жидкости, лежащей на поверхности тела, равна нулю, называется гипотезой прилипания. Она справедлива до тех пор, пока жидкость можно рас-сматривать как сплошную среду.

При обтекании неограниченным потоком жидкости плоской поверхности скорость жидкости вдали от нее равна , а на самой поверхности согласно гипотезе прилипания равна нулю (рис.2.1).

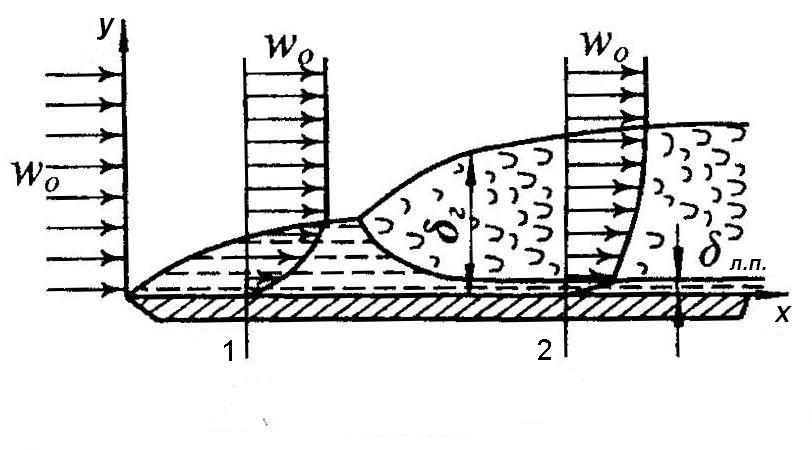
Рис.2.1 Схема движения жидкости при обтекании пластины

Следовательно, около поверхности вследствие действия сил вязкости, обра-зуется тонкий слой заторможенной жидкости, в пределах которого скорость изменяется от 0 до . Этот слой заторможенной жидкости получил наз-вание гидродинамического пограничного слоя. Поскольку скорость в погра-ничном слое приближается к асимптотически, то вводят следующее определение его толщины: толщиной гидродинамического слоя называ-ется расстояние от поверхности, на котором скорость отличается от на 1%.

По мере движения вдоль поверхности толщина пограничного слоя растет. Вначале образуется ламинарный пограничный слой, который с рос-том толщины становится неустойчивым и разрушается, превращаясь в тур-булентный пограничный слой. Однако и здесь вблизи поверхности сохра-няется тонкий ламинарный подслой ( ) в котором жидкость движется ламинарно. На рис. 2.1 показано изменение скорости в пределах ламинар-ного (сечение 1) и турбулентного (сечение 2) пограничных слоев.

Аналогично понятию динамического пограничного слоя Г.Н.Кружи-линым было введено понятие теплового пограничного слоя. Тепловой по-граничный слой - это слой жидкости у стенки, в пределах которого темпе-ратура изменяется от значения, равного температуре стенки, до значения, равного температуре жидкости вдали от тела. Следовательно, на стенках канала существует два пограничных слоя: динамический и тепловой. Необходимо отметить, что толщина обоих слоев уменьшается с увеличением скорости и плотности потока. Толщина динамического пограничного слоя увеличивается с повышением вязкости, а теплового - с увеличением коэф-фициента теплопроводности жидкости или газа. Установлено также, что соотношение толщин этих слоев определяется физическими свойствами теплоносителя: вязкостью, плотностью, теплоемкостью и коэффициентом теплопроводности. Толщина динамического пограничного слоя в жидкостях больше толщины теплового слоя. В расплавленных металлах, вследствие их высокой теплопроводности, толщина теплового пограничного слоя больше динамического. Для газов толщины этих слоев практически одинаковы. Поэтому в газовых потоках имеется подобие скоростных и температурных полей.

Конечной целью любого теплотехнического расчета конвективного теплообмена является определение количества теплоты в Дж, отдаваемого или воспринимаемого поверхностью твердого тела площадью 1 м² в течение 1 с. Эта величина обозначается буквой и называется удельным тепловым потоком или удельной тепловой нагрузкой.

Рассмотрим поле температур в турбулентном потоке и покажем, как в этом случае может быть определена величина удельного теплового потока. Характер изменения температур показан на рис.2.2. Из рисунка видно, что в ламинарном потоке, имеющем толщину , температура потока резко ме-няется от температуры стенки до температуры . В турбулентном подслое она падает от до температуры потока .

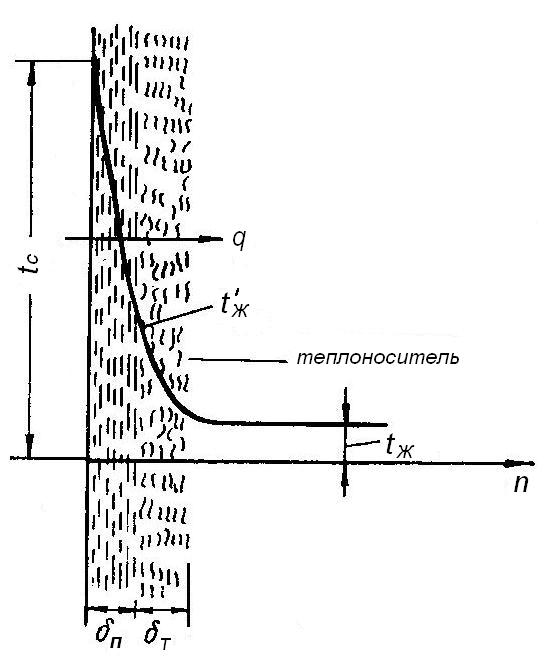
Рис.2.2 Пограничный слой теплоносителя: - вязкий подслой; -

турбулентный подслой

Учитывая, что через вязкий подслой теплота передается теплопро-водностью, величину удельного теплового потока, (Вт/м²) можно опреде-лить на основании следующего уравнения:

( - ), (2.1)

где - коэффициент теплопроводности потока, Вт/(м^оС); - толщина вяз-кого подслоя, м.

Суммарное количество теплоты , Вт, передаваемое всей поверх-ностью твердого тела , равно:

(2.2)

Чтобы из уравнения (2.1) определить , надо знать либо , либо . Однако простыми средствами эти величины измерить трудно, тем более, что они зависят от режима движения, от размеров и состояния поверхности нагрева, от условий входа и др. В силу этого изучение и расчет конвек-тивного теплообмена производится на основе закона Ньютона – Рихмана:

( - ) , (2.3)

где - коэффициент пропорциональности, называемый коэффициентом теплоотдачи, Вт/(м^{2 о}С).

Коэффициент теплоотдачи характеризует интенсивность теплообмена между поверхностью тела и окружающей средой. Числено он равен коли-честву теплоты, отдаваемой (или воспринимаемой) единицей поверхности в единицу времени при разности температур между поверхностью тела и ок-ружающей средой, равной одному градусу.

Внешний вид уравнения Ньютона-Рихмана кажется проще, чем уравнения (2), но в последнем случае вся тяжесть расчетов переносится на правильный выбор величины коэффициента теплоотдачи. Следует отме-тить, что величина меняется в очень широких пределах от 10 Вт/(м^2оС) до 10⁶ Вт/(м^2оС), что налагает особую ответственность на ее выбор.

Приравняв уравнения (2.2) и (2.3), можно получить:

Это соотношение удобно использовать для качественной оценки влияния некоторых факторов на величину коэффициента теплоотдачи конвекцией. Так, например, увеличение скорости движения потока приведет к увеличению турбулентности и уменьшению толщины вязкого подслоя, а следовательно, к увеличению коэффициента теплоотдачи. Увеличение вяз-кости потока приводит к увеличению толщины вязкого подслоя. Меняя ко-эффициент теплопроводности потока можно при прочих равных условиях менять величину коэффициента теплоотдачи конвекцией.