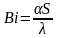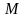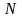- •Теплопроводность. Конвекция
- •1.Теплопроводность
- •1.1.Общие положения
- •1.1.1.Температурное поле
- •1.1.2. Температурный градиент
- •1.1.3. Тепловой поток. Закон Фурье
- •1.1.4.Коэффициент теплопроводности
- •1.1.5. Общее дифференциальное уравнение теплопроводности
- •1.1.6. Условие однозначности решения
- •1.2.Стационарная теплопроводность
- •1.2.1.Теплопроводность плоской стенки при граничных условиях первого рода
- •1.2.2. Теплопроводность плоской стенки при граничных условиях третьего рода (теплопередача через плоскую стенку)
- •1.2.3. Критический диаметр тепловой изоляции
- •1.2.4. Способы интенсификации теплопередачи
- •1.3.Нестационарные процессы теплопроводности
- •1.3.1.Физическая сущность процессов
- •1.3.2.Решение дифференциального уравнения теплопроводности в критериальном виде
- •1.3.3.Понятие тонкого и массивного тела
- •1.3.4.Нагрев тел при граничных условиях третьего рода
- •1.3.5.Анализ решения уравнения Фурье
- •1.4.Примеры решения задач по разделу «Теплопроводность»
- •2. Конвекция
- •2.1.Общие сведения о конвективном теплообмене
- •2.2. Математическое описание конвективного теплообмена
- •2.3.Критериальные уравнения конвективного теплообмена
- •2.4. Теплоотдача при свободной конвекции
- •2.4.1. Характер свободного движения потоков в большом объеме
- •2.4.2.Расчетные зависимости конвективного теплообмена в большом объеме
- •2.4.3.Теплообмен свободной конвекцией в ограниченном объеме
- •2.5.Конвективный теплообмен при вынужденном движении теплоносителя
- •2.5.1. Факторы, влияющие на конвективный теплообмен при вынужденном движении теплоносителя
- •2.5.2. Расчетные зависимости для определения коэффициентов теплоотдачи при вынужденном движении теплоносителя в каналах круглого сечения
- •2.5.3. Конвективный теплообмен при вынужденном внешнем обтекании тел
- •2.6.Примеры решения задач по разделу «Конвекция»
1.3.4.Нагрев тел при граничных условиях третьего рода
Рассмотрим
простейший случай нагрева плоской
неограниченной стенки, толщина которой
значительно меньше двух других ее
размеров. Стенка, имеющая по сечению
температуру
 внезапно нагревается средой постоянной
температуры
внезапно нагревается средой постоянной
температуры
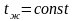 (рис.1.9). Выведем аналитические зависимости,
позволяющие определять температурное
поле пластины в лю-бой момент времени.
Используем уравнения:
(рис.1.9). Выведем аналитические зависимости,
позволяющие определять температурное
поле пластины в лю-бой момент времени.
Используем уравнения:
(1.48)
 (1.49)
(1.49)
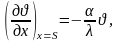 (1.50)
(1.50)
где
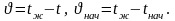
Уравнения (1.49) и (1.50) определяют краевые условия задачи.
Решая систему уравнений (1.48) - (1.50), было получено выражение
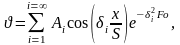 (1.51)
(1.51)
где
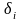 - корни уравнения
,
причем таких корней бесконечное
множество.
- корни уравнения
,
причем таких корней бесконечное
множество.
Учитывая,
что
 то уравнение (1.51) примет вид:
то уравнение (1.51) примет вид:
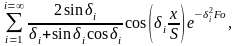 (1.52)
(1.52)
где

Для
средней плоскости пластины, т.е. при
 уравнение (1.52) имеет вид:
уравнение (1.52) имеет вид:
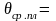
 (1.53)
(1.53)
для
поверхности пластины при
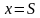
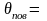
 (1.54)
(1.54)
Выражение средней по массе температуры пластины приводится без вывода. Это уравнение позволяет определить количество теплоты воспри-нятой пластиной в процессе нагрева:

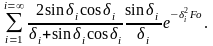 (1.55)
(1.55)
Уравнения
(1.53)-(1.55) представляют собой очень быстро
сходящиеся ряды. Сходимость их возрастает
вместе с увеличением
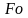 .
Даже при
.
Даже при
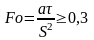 ряд может быть заменен первым членом.
Такой режим нагрева называется
регулярным. В этом случае для пластины
ряд может быть заменен первым членом.
Такой режим нагрева называется
регулярным. В этом случае для пластины
 (1.53/)
(1.53/)
 (1.54/)
(1.54/)
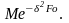 (1.55/)
(1.55/)
Значения
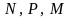 можно найти в табл.1.1, составленной
Д.В.Будриным. В этой таблице приведены
значения
можно найти в табл.1.1, составленной
Д.В.Будриным. В этой таблице приведены
значения
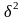 в зависимости от
.
По данным табл.1.1 построены графики
расчета нагрева или охлаждения средней
плос-кости, массы и поверхности пластины
(рис.1.10-1.12).
в зависимости от
.
По данным табл.1.1 построены графики
расчета нагрева или охлаждения средней
плос-кости, массы и поверхности пластины
(рис.1.10-1.12).
1.3.5.Анализ решения уравнения Фурье
Проведем
его на примере пластины. Рассмотрим
общее уравнения распределения температур
при
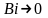 и
и
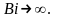
Из табл.1.1 видно, что значения незначительно отличаются друг от друга и близки к единице. Следовательно,
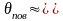

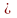
 (1.56)
(1.56)
Таким образом, при малых значениях температура внутри тела и на его поверхности практически одинакова. В этом случае скорость нагревания или охлаждения мало отличается от скорости нагревания или охлаждения тонкого тела, обладающего бесконечно большой теплопроводностью.
Выведем уравнение для определения времени нагрева тонкой пластины. Для этого преобразуем уравнение (1.56). Согласно табл.1.1 при
= . Получаем
 (1.57)
(1.57)
где
 - критерий Михеева, представляющий
собой произведение
- критерий Михеева, представляющий
собой произведение
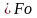 .
Преобразовав это уравнение в отношении
времени нагрева, получим
.
Преобразовав это уравнение в отношении
времени нагрева, получим
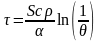 . (1.57/)
. (1.57/)
Вывод последнего уравнения легко показать на примере преобразования выражения (1.56)


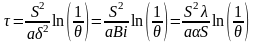
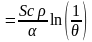 .
.
Из
этого уравнения видно, что время нагрева
или охлаждения тонкого тела пропорционально
линейному размеру в первой степени.
Если произ-вести аналогичные выводы
для цилиндра и шара, то окажется, что
при
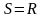 цилиндр нагревается или охлаждается
в два раза, а шар в три раза быстрее
пластины.
цилиндр нагревается или охлаждается
в два раза, а шар в три раза быстрее
пластины.
Таблица 1.1
Коэффициенты для расчета нагрева или охлаждения
пластины толщиной
|
|
|
|
|
|
|
|
|
|
0,00 0,01 0,02 0,04 0,06 0,08 0,10 0,12 0,14 0,16 0,18 0,20 0,22 0,24 0,26 0,28 0,30 0,35 0,40 0,45 0,50 0,55 0,60 0,70 0,80 0,90 1,00 1,20 1,40 1,60 1,80 2,00 |
0,000 0,0100 0,0199 0,0397 0,0584 0,0778 0,0968 0,1154 0,1337 0,1518 0,1697 0,1874 0,2048 0,2220 0,2390 0,2558 0,2723 0,3125 0,3516 0,3894 0,4264 0,4624 0,4970 0,5640 0,626 0,684 0,740 0,841 0,931 1,016 1,090 1,162 |
1,000 0,997 0,993 0,987 0,981 0,974 0,967 0,960 0,954 0,948 0,942 0,936 0,930 0,924 0,918 0,912 0,906 0,891 0,877 0,863 0,849 0,836 0,823 0,798 0,774 0,751 0,729 0,689 0,653 0,619 0,587 0,559 |
1,000 1,000 1,000 1,000 1,000 1,000 1,000 1,000 1,000 1,000 1,000 1,000 1,000 0,999 0,999 0,999 0,999 0,998 0,998 0,997 0,996 0,995 0,994 0,992 0,990 0,998 0,986 0,981 0,977 0,972 0,968 0,964 |
1,000 1,002 1,003 1,006 1,010 1,013 1,016 1,020 1,023 1,026 1,029 1,031 1,034 1,037 1,040 1,042 1,045 1,052 1,058 1,064 1,070 1,076 1,081 1,092 1,102 1,111 1,119 1,134 1,148 1,159 1,169 1,179 |
2,0 2,2 2,4 2,6 2,8 3,0 3,5 4,0 4,5 5,0 5,5 6,0 7,0 8,0 9,0 10,0 12,0 14,0 16,0 18,0 20,0 25,0 30,0 35,0 40,0 50,0 60,0 70,0 80,0 90,0 100,0 - |
1,162 1,222 1,277 1,332 1,380 1,420 1,52 1,59 1,66 1,73 1,78 1,82 1,90 1,95 2,00 2,04 2,08 2,12 2,16 2,20 2,24 2,27 2,30 2,33 2,35 2,37 2,39 2,40 2,41 2,41 2,42 2,47 |
0,559 0,535 0,510 0,488 0,468 0,448 0,406 0,370 0,338 0,314 0,293 0,273 0,241 0,216 0,196 0,180 0,152 0,132 0,116 0,104 0,094 0,076 0,065 0,056 0,050 0,0400 0,0333 0,0286 0,0250 0,0222 0,0200 0,0000 |
0,964 0,960 0,956 0,952 0,948 0,944 0,935 0,926 0,919 0,912 0,906 0,901 0,892 0,885 0,879 0,874 0,866 0,859 0,855 0,851 0,847 0,841 0,836 0,832 0,829 0,826 0,824 0,822 0,820 0,819 0,818 0,810 |
1,179 1,186 1,193 1,200 1,205 1,210 1,221 1,229 1,235 1,240 1,244 1,248 1,254 1,257 1,260 1,262 1,265 1,267 1,268 1,269 1,270 1,271 1,271 1,272 1,272 1,272 1,273 1,273 1,273 1,273 1,273 1,273 |
Анализ
табл.1.1 и формулы (1.54/)
показывает, что при
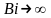 коэф-фициент
стремится к нулю. Следовательно,
коэф-фициент
стремится к нулю. Следовательно,
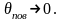 Таким образом, при больших значениях
поверхность тела очень быстро приобретает
темпе-ратуру, равную температуре среды.
Таким образом, при больших значениях
поверхность тела очень быстро приобретает
темпе-ратуру, равную температуре среды.
Этот случай возможен, если тело имеет очень большие размеры или большой коэффициент теплоотдачи (охлаждение или нагрев в жидких средах) и малый коэффициент теплопроводности.
Расчеты нагрева или охлаждения массивной пластины следует производить по уравнениям (1.53)-(1.55) или по графикам (см. рис.1.10-1.12).