1.4. Метод моментов и форма линии ямр

Важными характеристиками формы линий являются моменты линии. K-ый момент относительно частоты определяется следующей формулой:

(47)

где – функция формы линии.

Положим

тогда или для узких линий

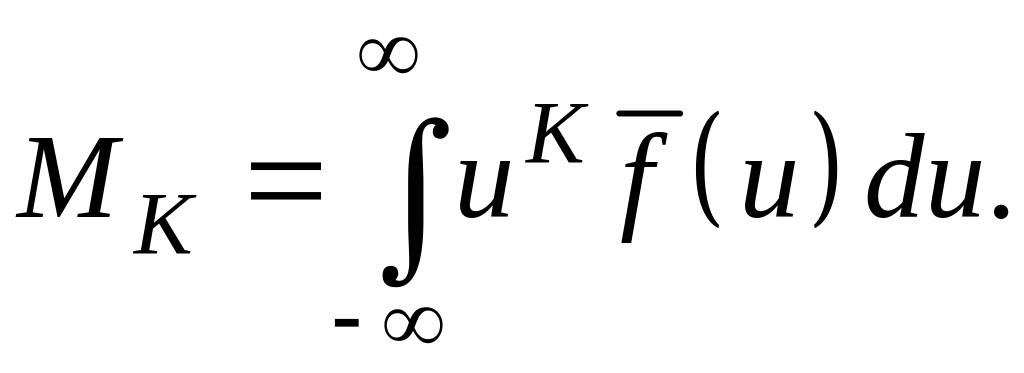(48)

Разложим в интеграл Фурье:

(49)

Фурье-образ функции формы линии имеет простой физический смысл. Пусть ядерный парамагнетик находится в равновесном состоянии в постоянном магнитном поле Н, так что его намагниченность направлена по полю. Если на образец наложить короткий интенсивный импульс радиочастотного поля то под его воздействием намагниченность повернётся на некоторый угол  к полю Н. Допустим, что длительность импульса настолько мала, что можно пренебречь явлениями релаксации. Если бы резонансная линия была бесконечно узка, то после прекращения импульса намагниченность М совершала бы прецессию с частотой вокруг поля под постоянным углом .

Эта свободная прецессия может быть детектирована по индуцированному ею сигналу в катушке, окружающей образец. Если ширина линии конечна, то вследствие разброса прецессионных частот сигнал затухнет за время порядка обратной ширины линии. Оказывается, что Фурье-образ функции формы линии просто связан с кривой затухания свободной прецессии: функция пропорциональна амплитуде сигнала свободной прецессии по окончании 90⁰-импульса.

Разложим функцию в ряд Тейлора вблизи точки

(50)

Из (49) вытекает, что

, (51)

и, следовательно, если известны все моменты , то может быть восстановлена функция формы Существуют методы, позволяющие с большой точностью рассчитать моменты , однако с ростом К вычисления становятся настолько громоздкими, что приходится ограничиться расчётом лишь нескольких первых моментов. Поэтому для сопоставления теории с экспериментом пользуются несколькими типичными кривыми, из которых выбирают наиболее близкую к линии, полученной из опыта. Затем остаётся сравнить известные моменты типичной кривой с моментами, полученными теоретически.

В качестве типичных кривых обычно пользуются следующими существенно различными функциями: гауссовой и лоренцевой.

У гауссовой линии

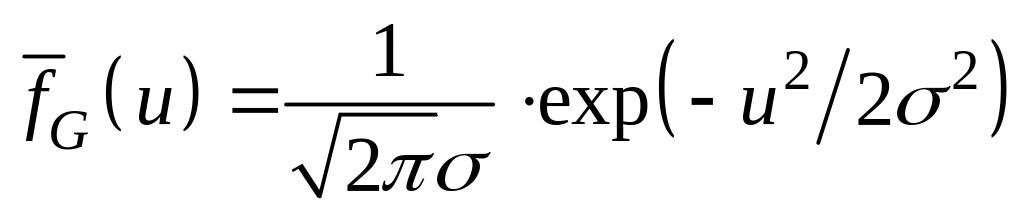(52)

вершина более полога, а крылья спадают быстрее, чем у лоренцевой:

(53)

Ширина линии, определяемая равенством

(54)

для гауссовой формы равна

а для лоренцевой:

Для гауссовой линии чётные моменты равны

(55)

Для лоренцевой линии интегралы (48) при К 1 расходятся. Поэтому лоренцеву линию обрезают на частотах где  /2.

Тогда

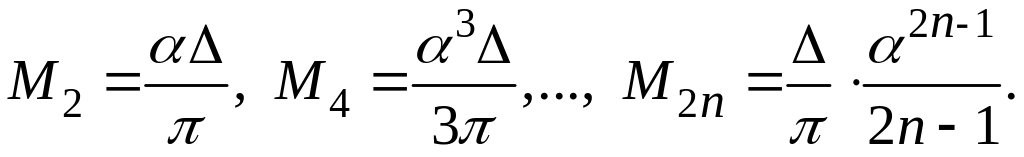(56)

Гауссова и лоренцева линии симметричны относительно ; поэтому нечётные моменты равны нулю. Для того чтобы выяснить, насколько близка та или иная функция формы к гауссовой или лоренцевой линии, часто ограничиваются вычислениями отношения Для гауссовой линии

(57)

для лоренцевой линии

(58)

для линии прямоугольной формы

1.5. Вычисление моментов

Вернёмся к ширине и форме линии, уширенной благодаря диполь-дипольному взаимодействию. Наиболее простым, представляющим интерес, является второй момент дипольно уширенной линии, который в соответствии с (47) может быть определён как

(59)

Из-за симметрии линии средняя частота равна резонансной частоте и поэтому

(60)

Пусть собственные значения гамильтониана  (39) суть . Так как переход между уровнями и характеризуется частотой

и интенсивностью, пропорциональной то

(61)

Легко показать, что эта формула может быть преобразована к виду

(62)

Действительно,

Так как след (шпур) матрицы инвариантен в отношении преобразования подобия, мы можем предположить, что матрица  диагональна, и тогда

и, следовательно,

Знаменатель формулы (62) преобразуется следующим образом:

Справедливость формулы (62) доказана. Эта формула, в отличие от (61), очень удобна для расчётов, ибо следы матриц могут быть легко вычислены, в то время как нахождение собственных значений матриц при большом N связано с огромными трудностями.

Очень важно иметь в виду следующее. В формуле (62) учитывается поглощение на всех частотах от 0 до . Выше указывалось, что помимо главной резонансной линии на частоте существуют дополнительные пики поглощения на частотах хотя эти пики слабы (они находятся далеко от центра основной линии), их вклад в моменты высокого порядка очень велик.

Поэтому, поскольку нас интересует только главная резонансная линия, в формуле (62) гамильтониан необходимо заменить “усечённым” гамильтонианом отбросив в операторе диполь-дипольного взаимодействия ту его часть, которая не коммутирует с и поэтому приводит к появлению дополнительных резонансных пиков поглощения. Из (44) вытекает, что

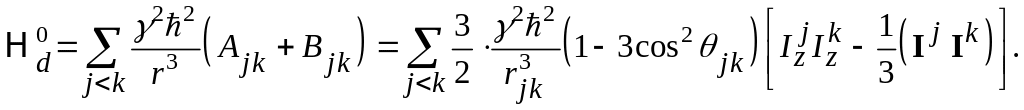(63)

Детальные расчёты моментов сводятся к вычислениям следов из произведений спиновых матриц

где Полезно иметь в виду, что

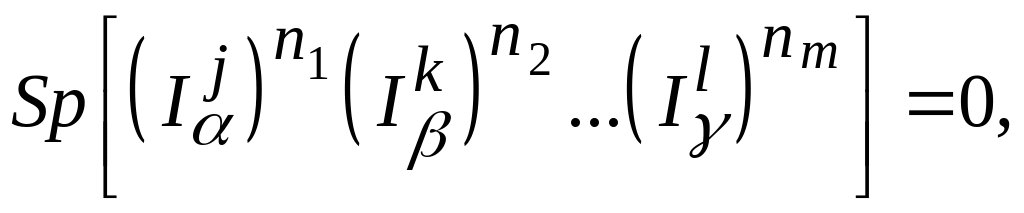(64)

если хотя бы одна из степеней является нечётным числом.

Воспользовавшись (64), нетрудно показать, что в (62) исчезают перекрёстные члены, содержащие произведения так что (62) переходит в следующую формулу:

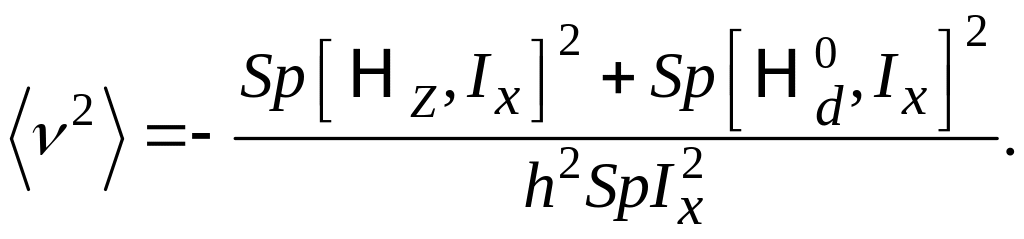(65)

Если бы не было диполь-дипольных взаимодействий и то, очевидно,

Из (60) и (65) получаем окончательно

(66)

Аналогично, для четвёртого момента имеем

(67)

Вычисления (66) с гамильтонианом (63) дают следующее выражение для второго момента (формула Ван-Флека):

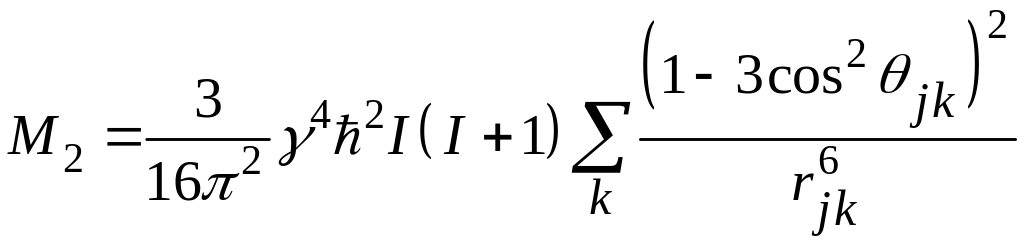[Гц²]. (68)

Для порошка, содержащего кристаллы с хаотическими ориентациями, это выражение упрощается благодаря исчезновению угловой зависимости. Усредняя по сфере, получаем и, следовательно,

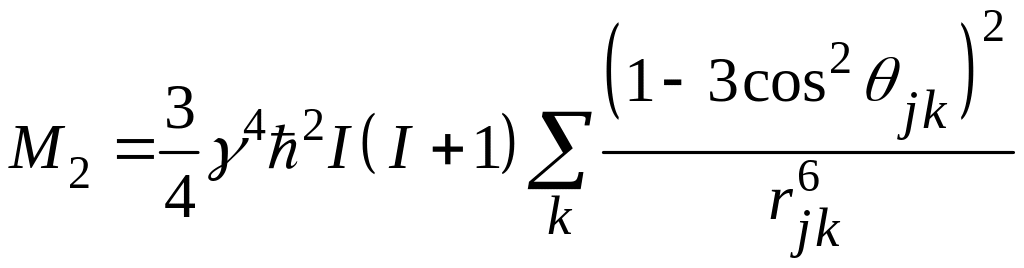[(радс) ²],

(69)

Для простой кубической решётки с постоянной имеем

и

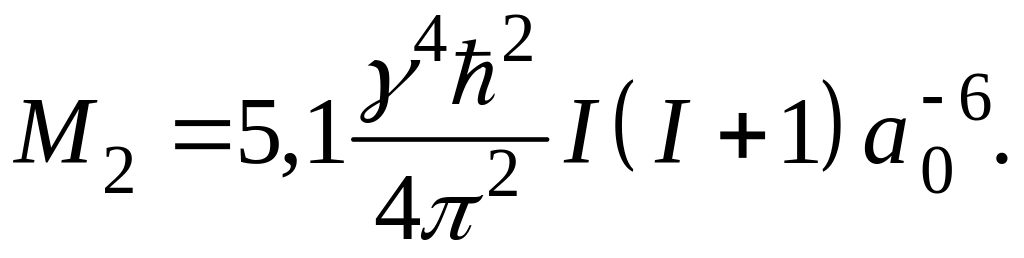(70)

В случае монокристалла с простой кубической решёткой

[Гц²], (71)

где – направляющие косинусы внешнего поля относительно осей кристалла; где – постоянная решётки.

Заметим, что с учётом в гамильтониане диполь-дипольного взаимодействия только статической части

второй момент получается в раз меньше. Если же, наоборот, мы включим в рассмотрение все операторы от A до F (см. (43)), то получим сильно завышенное значение. Простой расчёт показывает, что для порошка замена на полный гамильтониан приводит к увеличению в раз.

Зная только нельзя сделать выводы относительно формы резонансной линии. Поэтому, используя выражение (67), целесообразно вычислить ещё, по крайней мере, четвёртый момент. Результат этого громоздкого вычисления можно представить в виде:

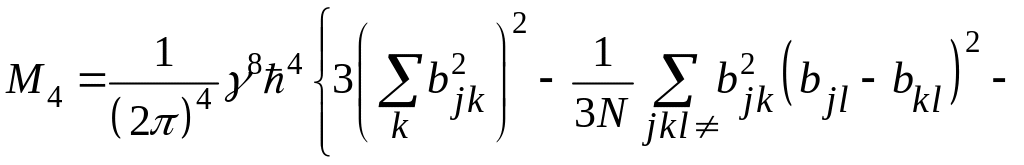
(72)

где

а символ означает, что в тройном суммировании не должно быть двух одинаковых индексов. Численная оценка (72) затруднительна даже для простой кубической решётки, если направление магнитного поля относительно кристаллографических осей произвольно. Если сохранить в фигурных скобках только первый член, то что отвечает гауссовой форме линии.