1.3. Диполь-дипольные взаимодействия в жёсткой решётке

Уширение резонансных линий обусловлено целым рядом физических причин. Самой простой из них является неоднородность приложенного постоянного магнитного поля. В обычных магнитах, создающих магнитные поля 10⁴ Гс, отклонение магнитного поля от среднего значения составляет несколько десятых долей гаусса; при помощи специальных сложных приспособлений это значение может быть снижено до нескольких миллигаусс. Однородность поля в пределах магнитного образца зависит от размеров образца. Обычно используются образцы, объёмы которых лежат в пределах от 0,1 см³ до нескольких кубических сантиметров.

Для ядер, обладающих электрическими квадрупольными моментами, может наблюдаться несколько резонансных линий. Появление таких линий связано с взаимодействием ядерного квадрупольного момента с электрическим полем кристалла. Это приводит к существенному уширению резонансных линий. Установление равновесных значений населённостей зеемановских уровней системы связано с переходами между этими уровнями под влиянием спин-решёточного взаимодействия. Благодаря таким переходам, время жизни системы на каком-либо одном уровне будет ограничено, что приводит к дополнительному уширению линии на величину в энергетических единицах.

В этом разделе мы пренебрежём всеми перечисленными выше эффектами и сосредоточим внимание на механизме уширения резонансных линий, связанном с диполь-дипольным взаимодействием между магнитными моментами различных ядер. Такое пренебрежение во многих случаях вполне допустимо. В частности, оно вполне оправдано в тех случаях, когда спины отдельных ядер равны (в этом случае квадрупольные моменты ядер равны нулю), а время спин-решёточной релаксации достаточно велико.

Вклад диполь-дипольных взаимодействий в ширину резонансных линий легко оценить по порядку величины. Если расстояние между соседними ядрами, обладающими магнитными моментами , равно r, то каждое ядро будет создавать в точке, где находится соседнее ядро, магнитное поле , по порядку величины равное

(36)

Если принять, что r = 2 Å и  = 10^{– 23} эрг/Гс (2 ядерных магнетона), то . Так как это поле может иметь различную ориентацию относительно постоянного поля , резонансные частоты отдельных ядер будут распределены в области шириной примерно 1 Гс. В этой же области будет наблюдаться резонансное поглощение энергии. Из этих рассуждений следует, что ширина резонансной линии не зависит от внешнего магнитного поля Н.

Классическое выражение для энергии взаимодействия двух магнитных моментов и имеет следующий вид:

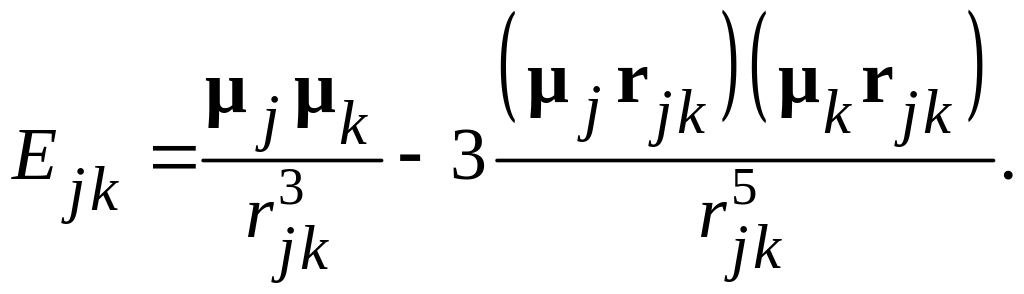(37)

Для получения квантово-механического гамильтониана взаимодействия

необходимо подставить в (37) вместо векторов и соответствующие операторы

(38)

Полный гамильтониан системы N одинаковых взаимодействующих спинов в сильном внешнем магнитном поле может быть записан в виде

(39)

где

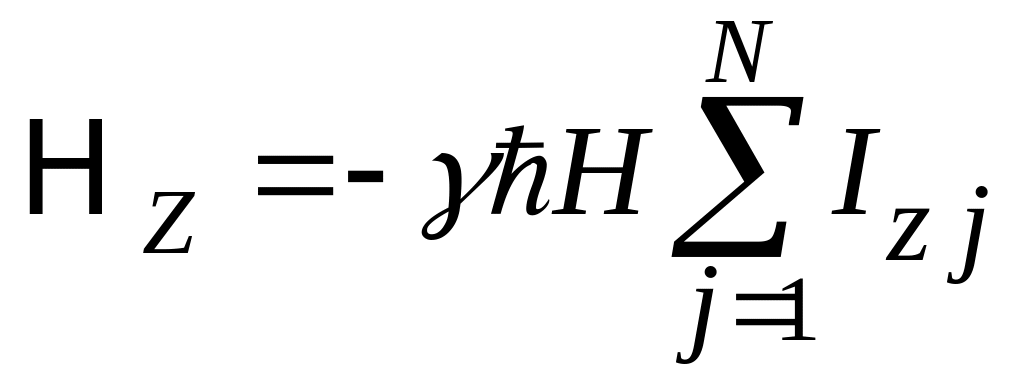(40)

– энергия во внешнем магнитном поле, а

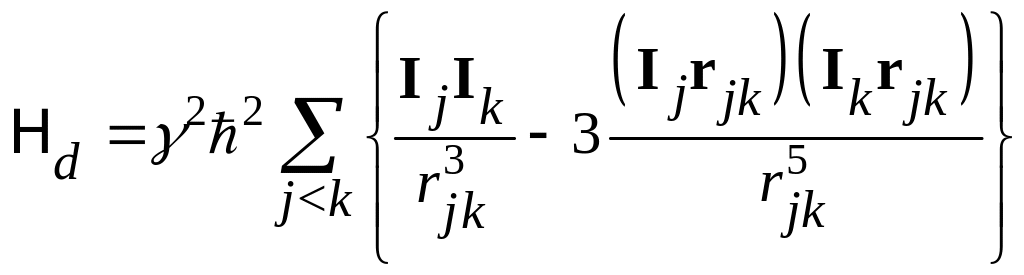(41)

– энергия диполь-дипольного взаимодействия.

В дальнейшем, чтобы сделать формулы менее громоздкими, там, где это не может вызвать недоразумение, опустим индексы j и k сферических координат r, , . Тогда

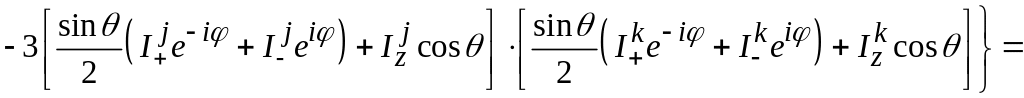
(42)

где

,

(43)

Рассмотрим взаимодействие j-ой и k-ой частиц. Допустим, что избрано такое представление, в котором z-компонента спина каждой частицы диагональна. Пусть и М – квантовые числа проекций и Нетрудно сообразить, что операторы (43) связывают состояния, различающиеся следующим образом:

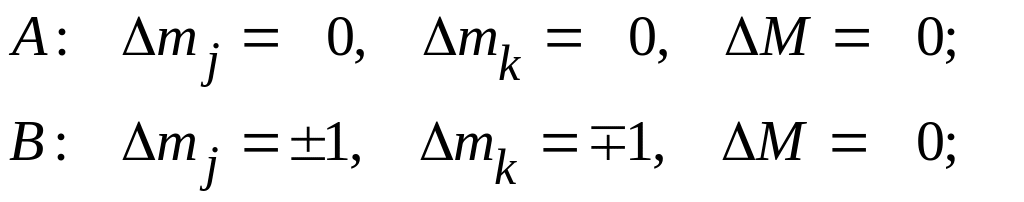
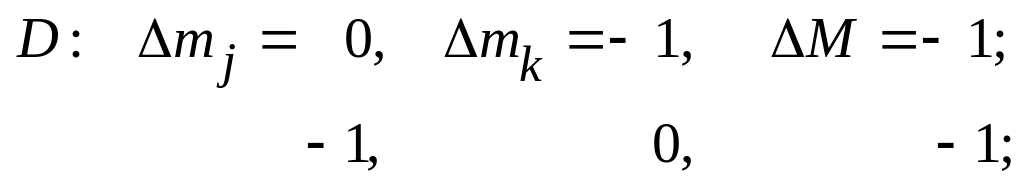
Мы видим, что матрицы А и В диагональны по М и коммутируют с матрицей зеемановской энергии (40).

Поскольку диполь-дипольное взаимодействие намного слабее зеемановского, естественно попытаться выяснить, какие заключения могут быть сделаны о спектре ЯМР и форме резонансных линий на основе теории возмущений. Рассмотрим энергетический уровень соответствующий гамильтониану(40). Этот уровень сильно вырожден, т.к. существует много способов, которыми можно скомбинировать отдельные значения чтобы получить величину

Возмущение, описываемое гамильтонианом _d, расщепляет уровень на много подуровней. Согласно первому приближению теории возмущений, вклад первого порядка в расщепление уровня дают лишь те члены гамильтониана возмущения, которые обладают отличными от нуля матричными элементами внутри множества т.е. те, которые, действуя на состояние не вызывают изменения величины М. Обращаясь к (44), мы видим, что только операторы А и В удовлетворяют этому условию и должны быть сохранены для вычисления поправок к энергии .

Член А имеет тот же вид, что и выражение для взаимодействия двух классических диполей, и описывает взаимодействие одного диполя со статическим локальным полем, создаваемым другим диполем.

Член В описывает взаимодействие, при котором возможно одновременное переворачивание двух соседних спинов в противоположных направлениях. Эта часть гамильтониана соответствует резонансному действию вращающегося локального поля.

Влияние члена С заключается в примешивании к состоянию с невозмущённой энергией малой доли состояния Таким образом, точное собственное состояние гамильтониана  следует представить в виде где – малая величина порядка

Под влиянием переменного магнитного поля между двумя зеемановскими уровнями и будут иметь место переходы с вероятностью, пропорциональной

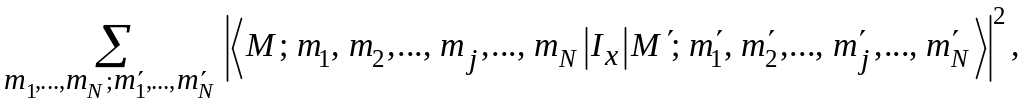(45)

где

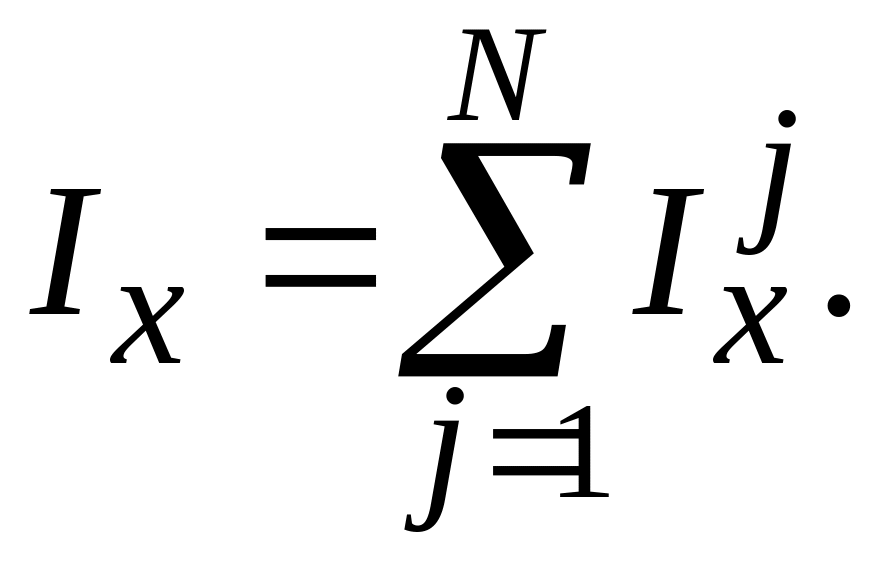
Из структуры матрицы ясно, что переходы

возможны только между соседними зеемановскими уровнями, что даёт одну резонансную линию на частоте

Этот вывод перестаёт быть справедливым, если перейти к следующему приближению теории возмущений. Действительно, с учётом операторов C, D, E и F правильные волновые функции можно представить в виде

(46)

где  Теперь становятся возможными переходы на частотах интенсивность дополнительных пиков поглощения пропорциональна .

Матрица А + В такова, что её структура не изменится, если у диагональных элементов изменить знак на обратный. Поэтому решение векового уравнения А + В – Е = 0 даёт для энергии возмущения Е значения, которые попарно одинаковы по модулю, но различаются по знаку. Легко сообразить, что вероятности перехода между двумя парами подуровней, отличающихся знаками энергии, также будут одинаковы. Отсюда вытекает, что форма основной линии ЯМР симметрична относительно резонансной частоты.

Проведение детальных расчётов методом возмущений невозможно из-за огромного числа степеней свободы системы магнитных частиц. Поэтому широкое применение нашёл метод моментов, позволяющий учесть магнитные дипольные взаимодействия и оценить форму резонансной линии, не производя вычислений энергетического спектра. Анализ формы линий магнитного резонанса методом моментов впервые был выполнен Ван-Флеком.