1.2. Магнитный резонанс в системах связанных спинов

1. Имея дело со связанной системой постоянных магнитных диполей, удобнее оперировать намагниченностью М или магнитным моментом всей системы, нежели магнитными моментами индивидуальных частиц. Магнитный момент всей системы представляет собой просто векторную сумму отдельных магнитных моментов. Поэтому в целом система спинов будет подчиняться классическому уравнению движения

(8)

Нас интересуют системы, в которых индивидуальные диполи слабо взаимодействуют друг с другом, т.е. такие, для которых статическая магнитная восприимчивость в приближении высоких температур H/kT 1 подчиняется закону Кюри:

(9)

(N – число частиц).

2. Особенности магнитного резонанса в системе связанных спинов мы учтём, отказавшись от предположения, что все изменения ориентации и величины намагниченности всецело обусловлены внешними магнитными полями, и приняв во внимание дополнительно два основных типа внутренних взаимодействий в конденсированных средах: 1) взаимодействие диполей с тепловыми колебаниями решётки и 2) взаимодействие их друг с другом. Оба этих взаимодействия обычно намного слабее зеемановского взаимодействия с внешними полями, но имеют значение благодаря их совокупному действию в течение длительных промежутков времени. Основное различие между ними состоит в том, что только первое взаимодействие (тепловые возмущения) может изменить энергию спин-системы, тогда как второе оставляет эту энергию неизменной.

Основную часть энергии спин-системы составляет зеемановская энергия в постоянном магнитном поле . Следовательно, основные изменения в энергии обязаны изменениям компоненты намагниченности . Предположим, что в какой-то момент времени компонента намагниченности не равна своему равновесному значению . Мы можем предположить (и это предположение оказывается хорошим приближением к действительности), что восстановление намагниченности происходит по экспоненциальному закону в соответствии с дифференциальным уравнением

(10)

Здесь – характеристическая постоянная времени, иногда называемая временем “продольной релаксации”, поскольку она определяет изменения -компоненты, параллельной постоянному магнитному полю. Часто эту константу называют временем “спин-решёточной релаксации”, поскольку она связана с обменом энергией между спин-системой и решёткой, в которую внедрены диполи.

Взаимодействие двух одинаковых диполей в сильном поле Н может быть описано с классической точки зрения следующим образом. Первый диполь прецессирует с ларморовой частотой вокруг поля Н и, следовательно, обладает постоянной составляющей вдоль этого поля и составляющей, которая вращается в плоскости, перпендикулярной полю. Постоянная составляющая создаёт в месте расположения диполя слабое постоянное поле ( ), ориентация которого относительно Н зависит от взаимного расположения спинов. Поскольку Н – сильное поле, то на него заметно влияет только параллельная или антипараллельная ему составляющая слабого поля. Каждый спин в решётке имеет несколько соседей с различными относительными положениями и ориентациями, поэтому постоянная составляющая локального поля имеет разные значения в различных местах, что приводит к разбросу ларморовских частот и уширению линии резонансного поглощения. Вращающаяся составляющая создает в месте расположения локальное магнитное поле, вращающееся с ларморовской частотой , которая совпадает с ларморовской частотой для . В свою очередь она имеет составляющую в плоскости, перпендикулярной Н, и, следовательно, может заметно изменить ориентацию благодаря явлению резонанса. Соответствующая ширина линии должна быть порядка величины вращающегося поля. В рассматриваемом случае оно того же порядка величины, что и локальное постоянное поле, и, следовательно, вносит в уширение вклад сравнимой величины.

3. Здесь следует остановиться на различии между однородным и неоднородным уширениями. Линия считается неоднородно уширенной, если ширина обусловлена разбросом ларморовских частот различных магнитных моментов в образце. Причины такого разброса разнообразны – от неоднородности внешнего магнитного поля до локальных изменений гиромагнитного отношения , вызванных взаимодействием диполей с их окружением. Какова бы ни была причина, неоднородное уширение имеет одну общую особенность: потеря фазовой когерентности, вызванная веерообразным расхождением индивидуальных прецессирующих диполей в плоскости xy, не является необратимой. Существует метод, известный под названием “спиновое эхо”, с помощью которого фазовая когерентность может быть восстановлена.

Если ширина линии в целом обусловлена релаксационными эффектами, то резонансная линия считается “однородно уширенной”. Прецессирующие компоненты дипольного поля индуцируют так называемые “флип-флоп” переходы, при которых один диполь теряет энергию, а другой приобретает её. Флип-флоп процесс наиболее эффективен тогда, когда диполи прецессируют с одинаковой частотой. При такой взаимной переориентации моментов суммарное значение сохраняется, и полная энергия системы остаётся неизменной. Полные значения и , напротив, не сохраняются; в результате переориентации спинов происходит постепенное разрушение фазовой когерентности между компонентами индивидуальных диполей в плоскости xy, и прецессирующая намагниченность в этой плоскости постепенно уменьшается до нуля. Флип-флоп процесс задаёт “истинное” время поперечной или спин-спиновой релаксации . Следуя Блоху, предположим, что компоненты намагниченности и подчиняются дифференциальным уравнениям

(11)

4. Как и раньше, мы предполагаем, что система спинов подвержена действию постоянного магнитного поля, направленного вдоль оси z, и поля вращающегося с частотой  в плоскости xy и имеющего компоненты Распишем уравнение движения намагниченности (8):

(12)

С учётом релаксационных эффектов они могут быть представлены в виде

(13)

Впервые эти уравнения были даны Блохом. Нужно отметить, что в отличие от уравнения (10), действительного для любого агрегатного состояния вещества, уравнения (11) справедливы, строго говоря, только для магнитных моментов, находящихся в быстром движении друг относительно друга, т.е. для жидкостей и газов. Из уравнения (11) следует, что спад амплитуды поперечной намагниченности во времени происходит по экспоненциальному закону. Можно показать, что экспоненциальный спад поперечной намагниченности  отвечает лоренцевой форме резонансной линии

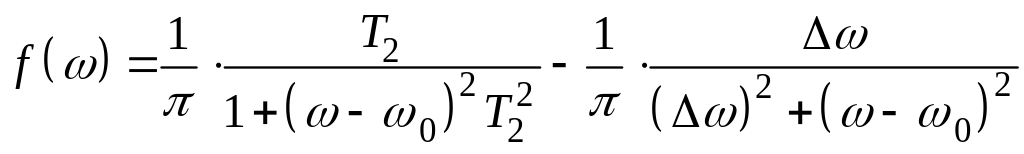(14)

( – ширина линии). Однако известно, что линии магнитного резонанса в твёрдых телах чаще всего имеют форму, близкую к гауссовой. Ниже мы получим решения уравнений движения намагниченности (13) для случая медленного прохождения через резонанс. Хотя эти решения нельзя считать адекватно описывающими магнитный резонанс в твёрдых телах, их можно использовать для анализа качественной стороны явления.

Будем искать стационарное решение, соответствующее вынужденной прецессии намагниченности вокруг постоянного магнитного поля с угловой скоростью приложенного поля :

(15)

В дальнейшем удобно заменить поперечные компоненты и на

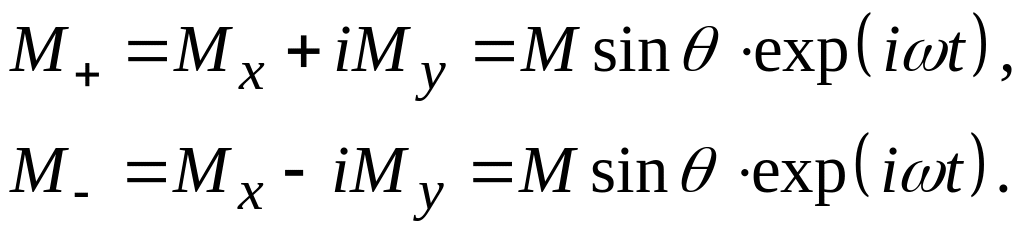(16)

Предположим, что скорость прохождения через резонанс очень мала, и во все моменты времени преобладают стационарные условия: или Тогда уравнения Блоха принимают такой вид:

(17)

Имея в виду, что

(см. (16)),

из первых двух уравнений (17) находим

(18)

Подставив эти решения в третье уравнение Блоха (17), получаем выражение для продольной намагниченности :

(19)

из которого видно, что компонента практически всегда равна и даже при резонансе отличается от мало, если  ²H₁²T₁T₂  1. Комбинация (18) и (19) даёт выражение для компонент поперечной намагниченности:

(20)

В целом, решения (19), (20) соответствуют прецессии вектора намагниченности вокруг поля Н под углом  к нему таким, что

(21)

В большинстве экспериментов прохождение через резонанс осуществляется путём изменения поля Н, а частота  сохраняется при этом постоянной. Поэтому величину tg удобно выразить через магнитные поля. Имея в виду, что – резонансное поле для частоты , а – ширина резонансной линии, мы можем переписать (21) в следующем виде:

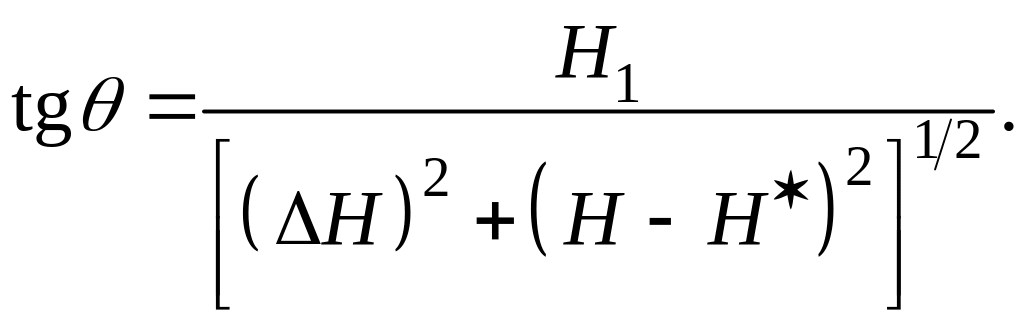(22)

Обычно, при изучении магнитного резонанса стационарным методом амплитуда осциллирующего поля выбирается намного меньше ширины линии; поэтому угол  даже при резонансе близок к нулю.

Выясним, как ведёт себя при резонансе проекция намагниченности на плоскость, перпендикулярную постоянному полю Н. Угол, который составляет эта проекция с вектором осциллирующего поля , можно найти из выражения

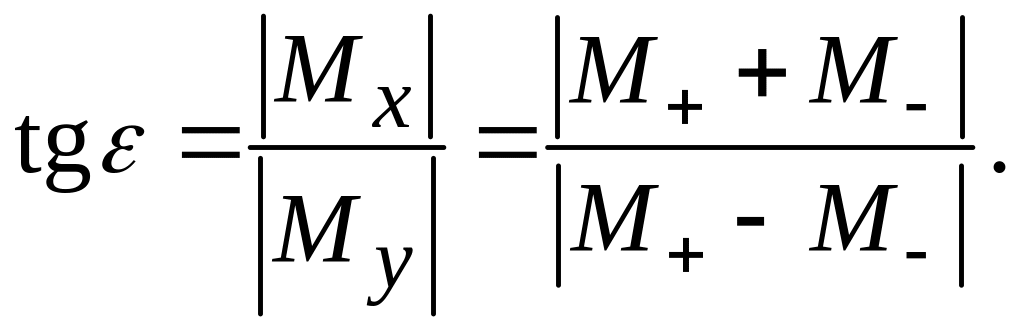(23)

Подстановка (18) в (23) даёт:

(23 a)

Таким образом, при прохождении резонанса ориентация вектора поперечной намагниченности относительно поля изменяется от параллельной до антипараллельной; при резонансе вектор поперечной намагниченности составляет с угол

5. Осциллирующая часть намагниченности может быть выражена через комплексную восприимчивость:

(24)

Пользуясь (24), запишем выражения для действительной и мнимой частей комплексной восприимчивости:

(25)

Подставив (20) в (25), получаем:

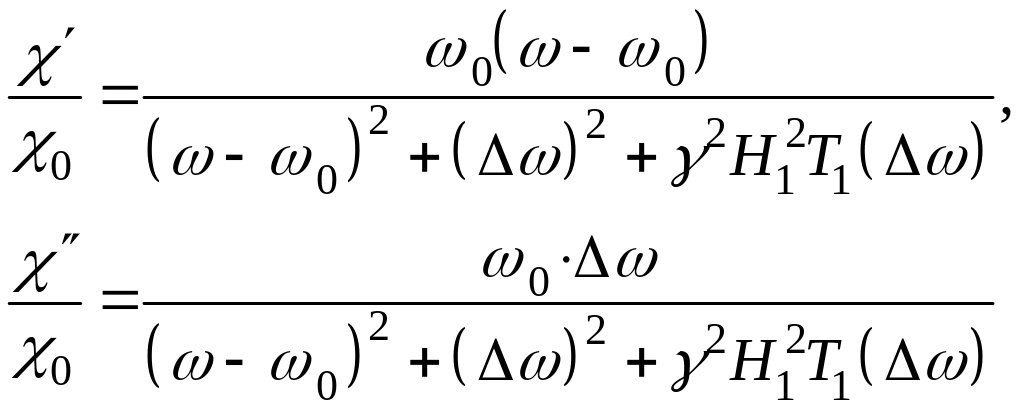(26)

(в формулах (26) использовано обозначение ).

Таким образом, действительная часть восприимчивости при резонансе равна нулю, а в стороне от резонанса она либо положительна (если ), либо отрицательна (если ). Мнимая часть восприимчивости при резонансе имеет максимум и, если , то

(27)

Это означает, что мнимая часть комплексной восприимчивости намного больше статической восприимчивости, если ширина линии мала по сравнению с резонансной частотой. Поэтому резонансные методы в раз чувствительнее статических.

6. Выше отмечалось, что при выполнении условия величина продольной компоненты намагниченности отличается от М₀ незначительно даже в момент резонанса. При резонансе величина

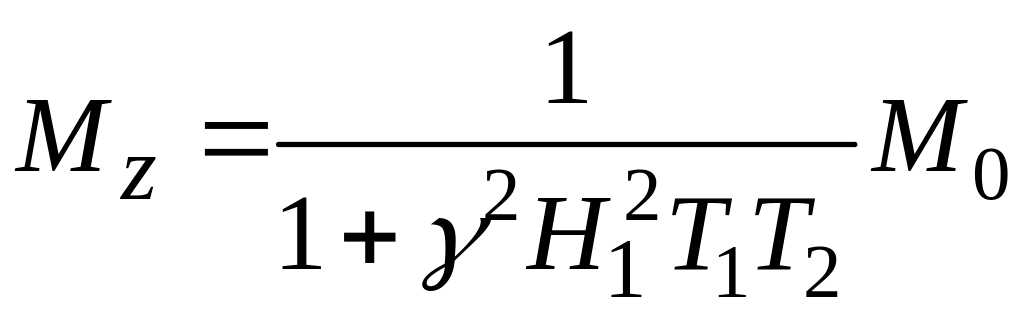(28)

может оказаться малой только вследствие эффекта насыщения резонансной линии сильным радиочастотным полем . Это происходит потому, что спин-система поглощает энергию осциллирующего поля с некоторой скоростью , и это поглощение повышает температуру спин-системы до тех пор, пока не сравняется со скоростью передачи энергии от спин-системы к решётке. Естественно, температура спин-системы возрастает с увеличением тем больше, чем длиннее времена спин-решёточной ( ) и спин-спиновой ( ) релаксаций.

7. Какова же скорость поглощения энергии радиочастотного поля спин-системой? Другими словами, какова поглощаемая мощность?

Имеем

(29)

где

Подставив в (29) выражения для компонент поперечной намагниченности

(30)

и произведя усреднение, получаем

(31)

Таким образом, мощность, поглощаемая при резонансе, пропорциональна мнимой части комплексной восприимчивости. По этой причине эту величину часто называют просто поглощением.

8. Частотная зависимость задаёт форму линии резонансного поглощения. В микроскопической теории показывается, что в общем случае мнимая часть комплексной восприимчивости связана со статической восприимчивостью соотношением

(32)

где – так называемая функция формы линии, удовлетворяющая условию нормировки:

(33)

При подходящем выборе функции формы линии выражение (32) подобно выражению (27), полученному нами из макроскопических уравнений. Действительно, формулу (27) легко получить из формулы (32), подставив в последнюю лоренцеву функцию формы (14).

9. В выражении (32), как мы видим, отсутствуют квантово-механические величины. Это является следствием так называемых соотношений Крамерса-Кронига, которые связывают действительную и мнимую части комплексной восприимчивости. Вывод этих соотношений приведен в монографии [1]. В применении к нашей задаче соотношения Крамерса-Кронига могут быть представлены в виде

(34)

Из первого соотношения следует, что статическая магнитная восприимчивость равна

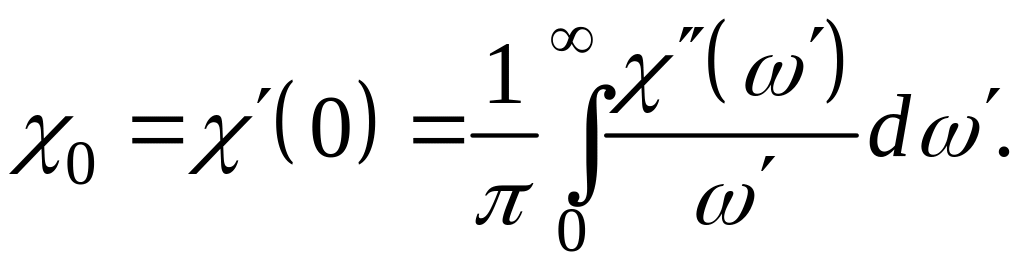(35)

Действительно, подставив в (35) мнимую часть восприимчивости из (32), получаем

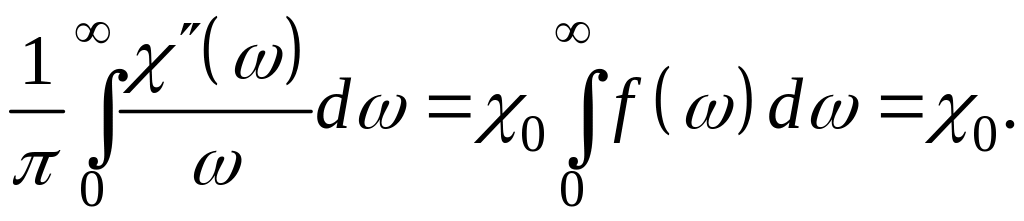
Здесь следует отметить, что формулы (26) для и , полученные нами из макроскопических уравнений движения намагниченности, содержат члены с и удовлетворяют соотношениям Крамерса-Кронига только в предельном случае малых . При больших амплитудах наступает насыщение, температура спин-системы становится выше температуры кристаллической решётки, и намагниченность перестаёт быть линейной функцией . Соотношения же Крамерса-Кронига справедливы только для линейных систем.