
5.3.3.2 Конустық бет
Жоғарыда атап өтілгендей, жалпы жағдайда конустық бет әрбір қалыпта құраушы ортақ S нүктесі арқылы өтетіндей және қандай да бір нүктеде бағыт-таушыны қиып өтетіндей, құраушының қисық сызықты бағыттаушы бойымен орын ауыстыруымен құрастырылады (49, б, 50-суреттер). Егер бағыттаушы шеңбер болып табылса, ал S нүктесі оның центріне перпендикулярда орналас-са, онда алынған бет «тік дөңгелек конус» немесе көпшіліктің түсінігінде «конус» деп аталады (48, б-сурет).
Кез-келген айналу беті сияқты, тік дөңгелек конус қаңқасының тірек сызықтары бас фронталь меридиан (63, а-суреттегі ФМ’, ФМ’’ қараңыз) және бас профиль меридиан (ПМ’, ПМ’’) болып табылады. Конустың шартты эква-торы оның негізі болып табылады. Бұл вертикаль конус бетіндегі кез-келген нүктелердің горизонталь проекцияларының көрінетін болып табылатынын білдіреді. Фронталь проекциялармен берілген, 1…5 нүктелердің жетіспейтін проекциялары, олардың әрқайсысының өзінің тірек сызығына тиесілігі бойын-ша сфераға ұқсас анықталады. Тірек сызықтарына тиесілі емес нүктелердің жетіспейтін проекциялары, құраушылар проекциялары арқылы да (63, б-сурет-тегі 1, 2 нүктелерді қараңыз), параллельдер проекциялары арқылы да анық-талуы мүмкін (3-нүкте). Студенттерге параллельдер проекциялары арқылы 1, 2 нүктелердің горизонталь проекцияларын, 3 нүктенің фронталь проекциясын құраушы проекциясы арқылы анықтау және нәтижелердің толық сәйкес келетініне көз жеткізу ұсынылады.
63,
а-сурет
63,
б-сурет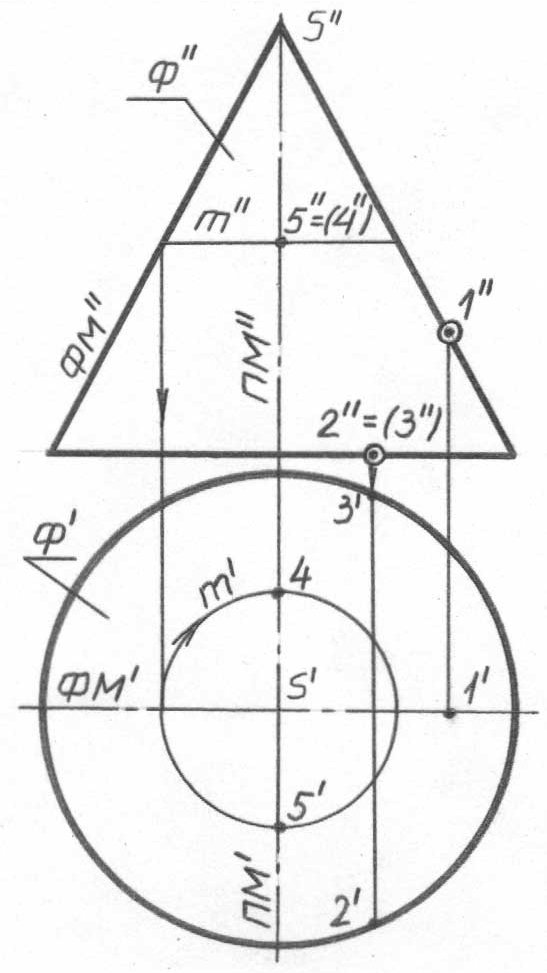
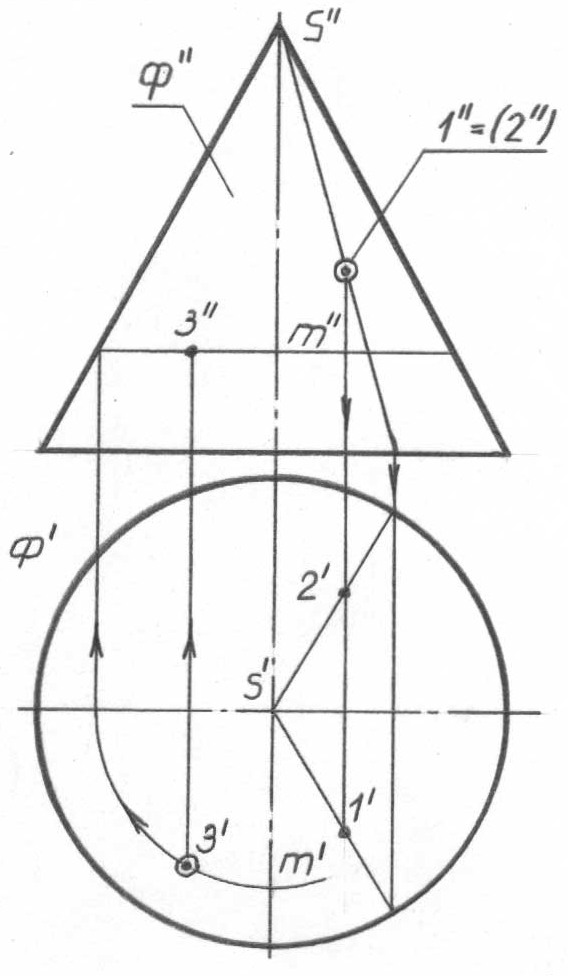
3.3.3 Цилиндрлік бет
Тік дөңгелек цилиндр бетін құрастыру мәселесі бұрын қарастырылған. Бет қаңқасының тірек сызықтары 64-суретте берілген (ФМ’, ФМ’’, ПМ’, ПМ’’ қараңыз). Бұл бетте экватордың жоқ екендігін атап кетейік. Осы бетпен байланысты, оларға тән кейбір моменттер келесіге келтіріледі.
Б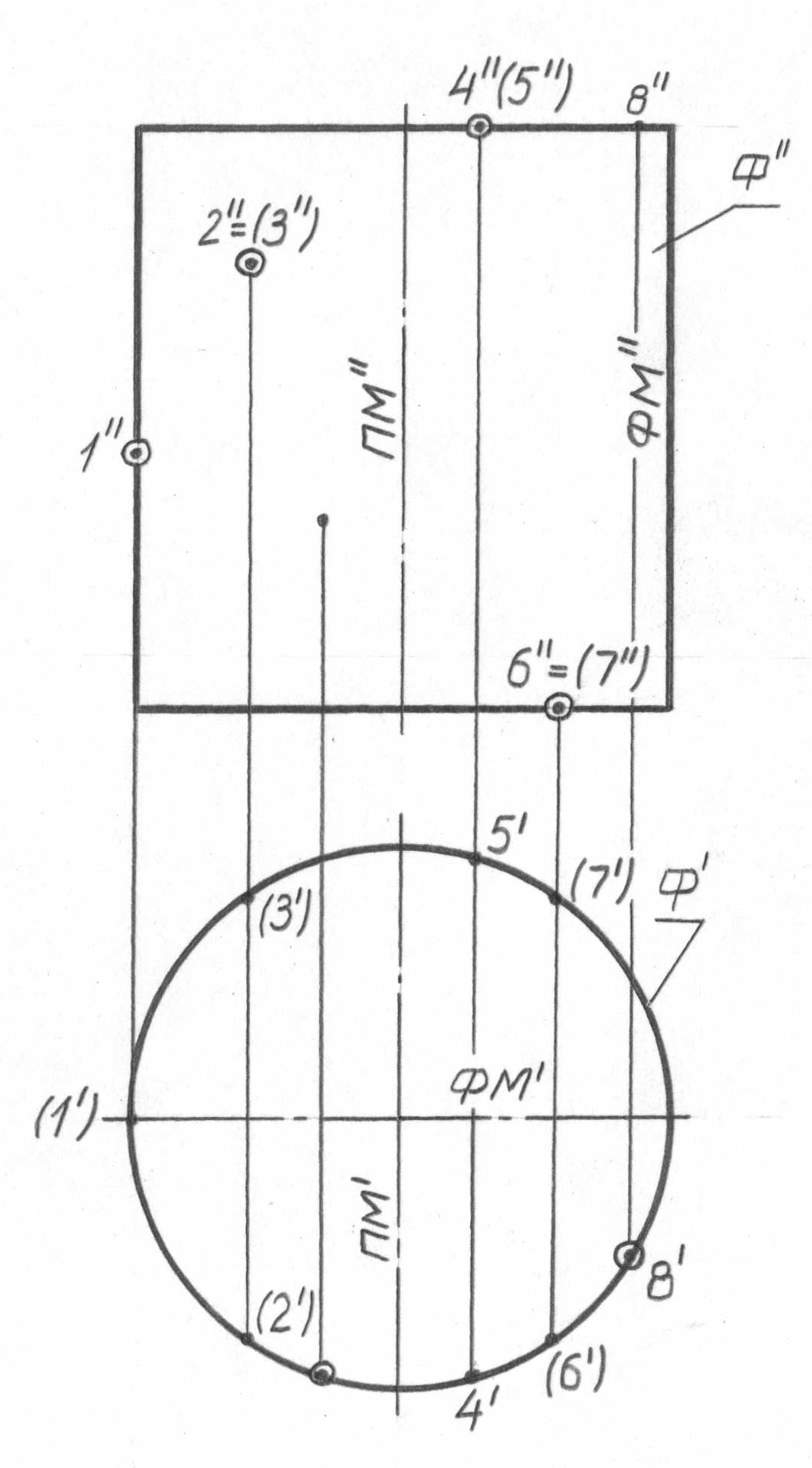 іріншіден,
горизонталь проекция-да, жоғарғы қиықта
орналасқандардан (4, 5, 8) басқа, барлық
нүктелер көрінбейтін болады.
іріншіден,
горизонталь проекция-да, жоғарғы қиықта
орналасқандардан (4, 5, 8) басқа, барлық
нүктелер көрінбейтін болады.
Екіншіден, мұндай цилиндрдің кез-келген құраушысы горизонталь-проекциялаушы сызық (тік призмадағы сияқты) болып табылатындықтан, беттің кез-келген нүктелерінің горизонталь проекциялары оның Ф’ горизонталь очеркінде ғана көрсетілетін болады және одан түсе алмайды.
Үшіншіден, 8 нүктенің горизон-таль проекциясы (көрінетін), нүктенің беттің жоғарғы қиығында орналасқаны туралы айтады.
Т
64-сурет
5.4 Беттің жеке орналасқан жазықтықпен қимасы
5.4.1 Жалпы ескертулер
Ұсынылып отырған тақырып студенттерді оқу курсының «Проекциялық сызу» графикалық модулін орындауға теориялық дайындаудың элементі болып табылады. Оны әр түрлі беттерге қатысты бірнеше бір типті есептерді шешу мысалдарында қарастырамыз. Есептің жалпыланған тұжырымдамасы келесі түрде болады: «беттің жеке орналасқан жазықтықпен қиылысуы фигурасының проекциясын және нақты көлемін салу». Есеп шартының жалпыланған формулалы жазбасы мынадай болады:
![]()
Беттің жазықтықпен қиылысуының l сызығының жазықтық пен бет үшін ортақ, жеке нүктелер бойынша салынатынын алдын-ала байқаймыз. Салуды оларға тән нүктелерден: жоғарғы, төменгі, жақын, алыс, сол, оң, көрінушілік аймақтары шекараларынан бастау керек. Егер оларға тән нүктелер ізделіп отырған қисықтың пішінін айқындау үшін жеткіліксіз болып табылса, кәдімгі (қатардағы) нүктелердің бірнеше жұбын табады. Нүктелердің көрінушілігі және оларды қосу тізбектілігі туралы мәселені шешеді. Кез-келген есепте оларға тән нүктелердің әрқайсысын тура салумен анықтауға болатынын атап кету керек. Бұл жағдайда тән нүктенің болжанып отырған облысында бірнеше қосымша нүктелерді беруге және олар арқылы оның орнын нақтылауға болады.
5.4.2 Сфераның жеке орналасқан жазықтықпен қиылысуы
Материалды түсінуді жеңілдету үшін l сызығын салу процесі бірнеше графикалық фрагментке бөлінген (65, а-г-сурет). «Тақырыпқа кіру» тәртібінде кеңістікте және проекцияларда ізделіп отырған l сызығының пішіні туралы
65, а-сурет
Рис. 65б
Рис. 65г
65, б-сурет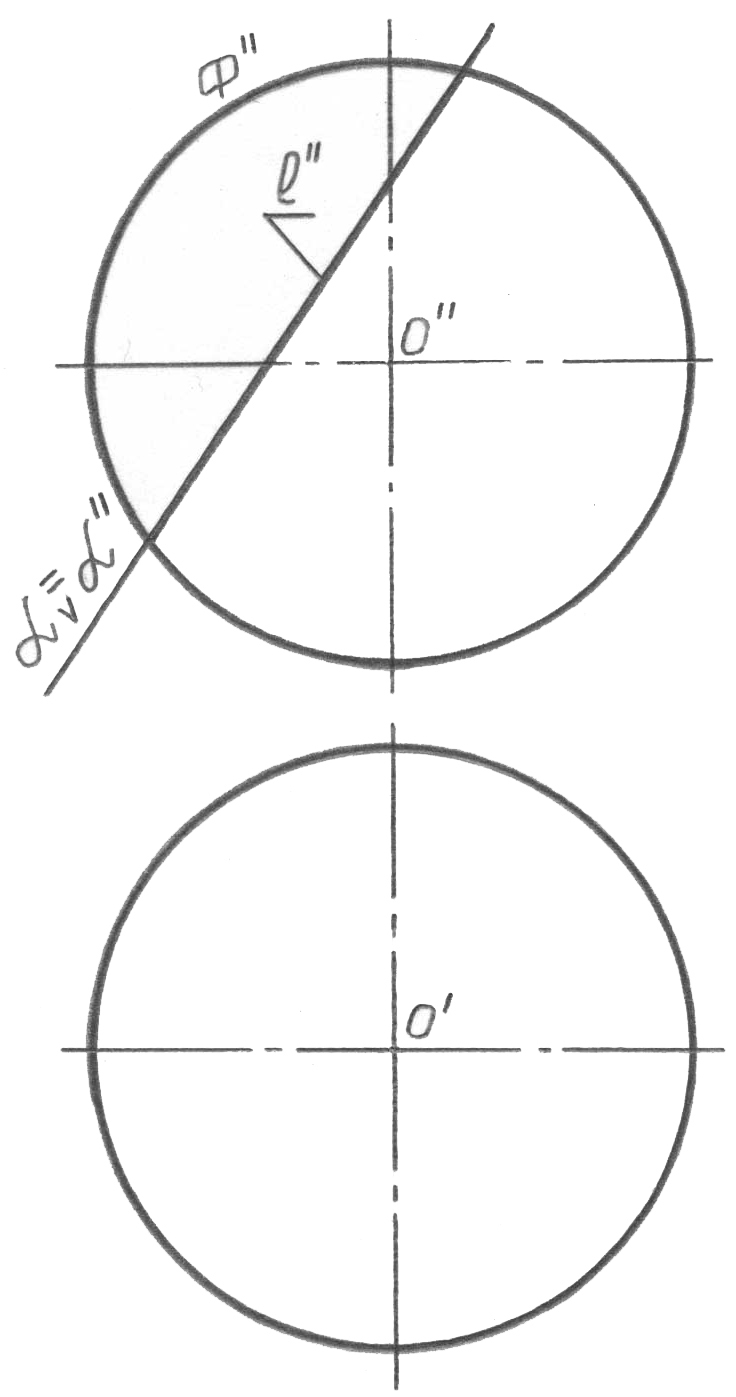
65, в-сурет
65, г-сурет
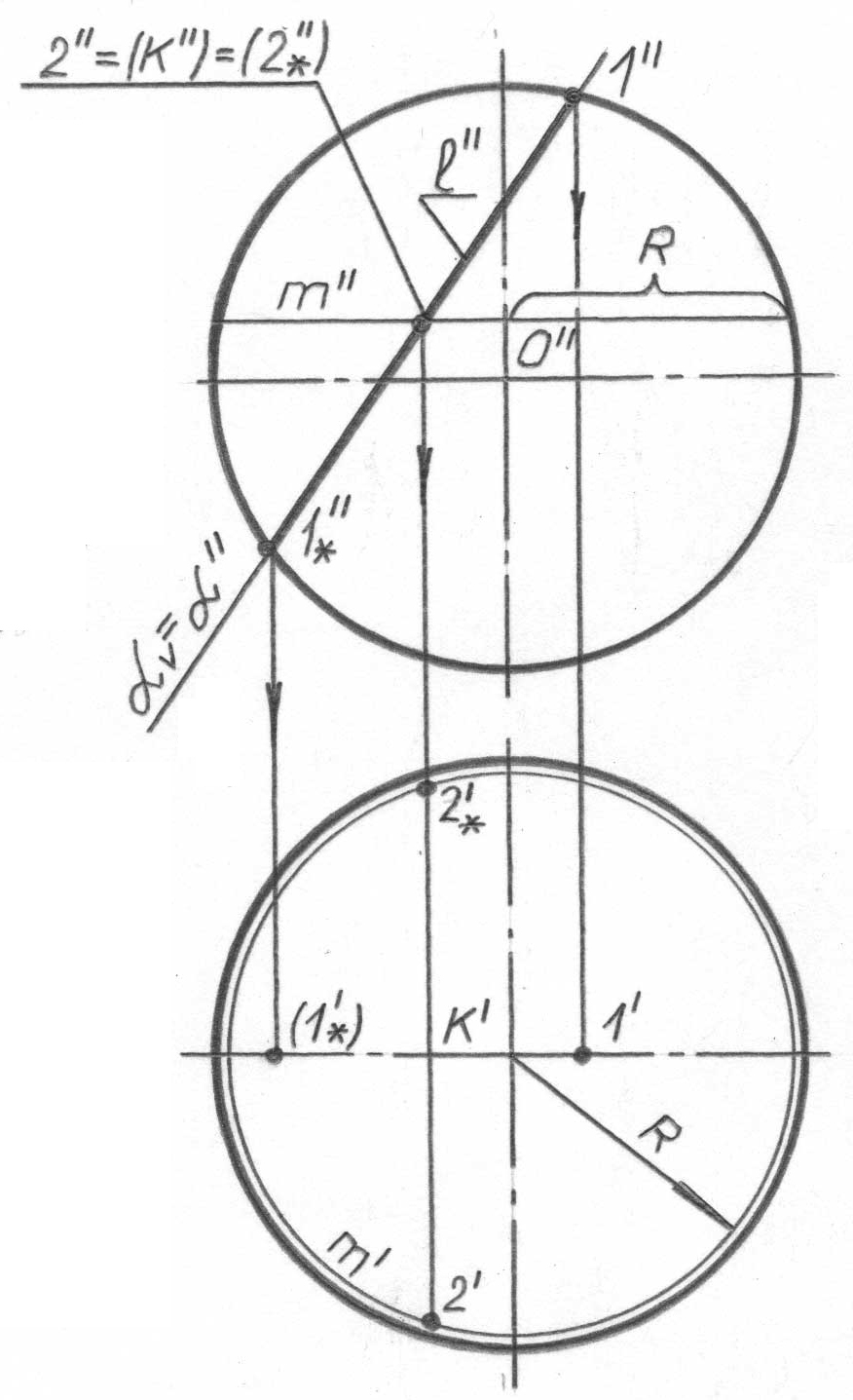
сұраққа жауап беруге тырысамыз. Сонымен бірге сфераның кез-келген жанама емес жазықтықпен қиылысуында шеңбер болатынын еске түсірген пайдалы. Біздің есебімізде (65, а-сурет) жазықтығы фронталь жазықтыққа перпен-дикуляр. Бұдан шығатыны: l шеңберінің l’’ фронталь проекциясы, ізбен - жазықтығының проекциясымен сәйкес келетін, сфера очеркінің ішіндегі түзу болады (есіңізге түсіріңіз: «проекциялаушы жазықтықта орналасқан, кез-келген нүкте, сызық немесе жазық фигура, оның із-проекциясында көрсетіледі», ал l сызығы бетке де, жазықтығына да тиесілі болады). l сызығының горизонталь проекциясы эллипсті білдіреді, өйткені жазықтығы проекцияның горизонталь жазықтығына параллель емес. Сөйтіп, есеп H горизонталь жазықтығында l шеңберінің бір мағыналы анықталған l’’ = V = ’’ фронталь проекциясы бойынша l эллипсін салуға келтіріледі.
65, а-суреттен 1 нүктесінің - l сызығының жоғарғы оң нүктесі, ал 1* төменгі сол нүктесі болып табылатыны көрініп тұр. Олардың 1’’ және 1*’’ проекциялары - Ф’’ бас фронталь меридианның фронталь проекциясында (62, б, г-суретті қараңыз) жатқандықтан, 1’ және 1*’ нүктелердің горизонталь проекциялары фронталь меридианның горизонталь проекциясында орналасу керек (65, б-сурет). 1* нүктесі экватордың астында орналасқандықтан, горизонталь проекцияда ол көрінбейтін (1*’) болады. 1’-(1*’) кесіндісі дегеніміз ізделіп отырған эллипстің кіші осі. Эллипс симметриялы фигура болып табылатындықтан, оның осьтері өзара перпендикуляр және бір-бірін жартыға бөледі. Бұдан, 1'-(1*') және 1'’-(1*'’) кесінділерін жартыға бөліп (65, б-сурет), осьтер қиылысуының k нүктесінің k’ және k’’ проекцияларын аламыз және сонымен бірге үлкен осьтің горизонталь (1'-(1*') перпендикуляр) және фронталь (2’’ = (k’’) = (2*’’)) проекциялардағы бағытын аламыз. Горизонталь проекция-дағы эллипстің үлкен осінің 2 және 2* ұштарын оған m’’ фронталь проекциясы 2’’ = (k’’) = (2*’’) нүктесі арқылы алдын ала жүргізілетін, m параллелінің көмегімен анықтаймыз. Сонымен бірге 2 нүктесінің - ең жақын, ал 2* нүктесінің ең алыс болып табылатынын атап кетеміз.
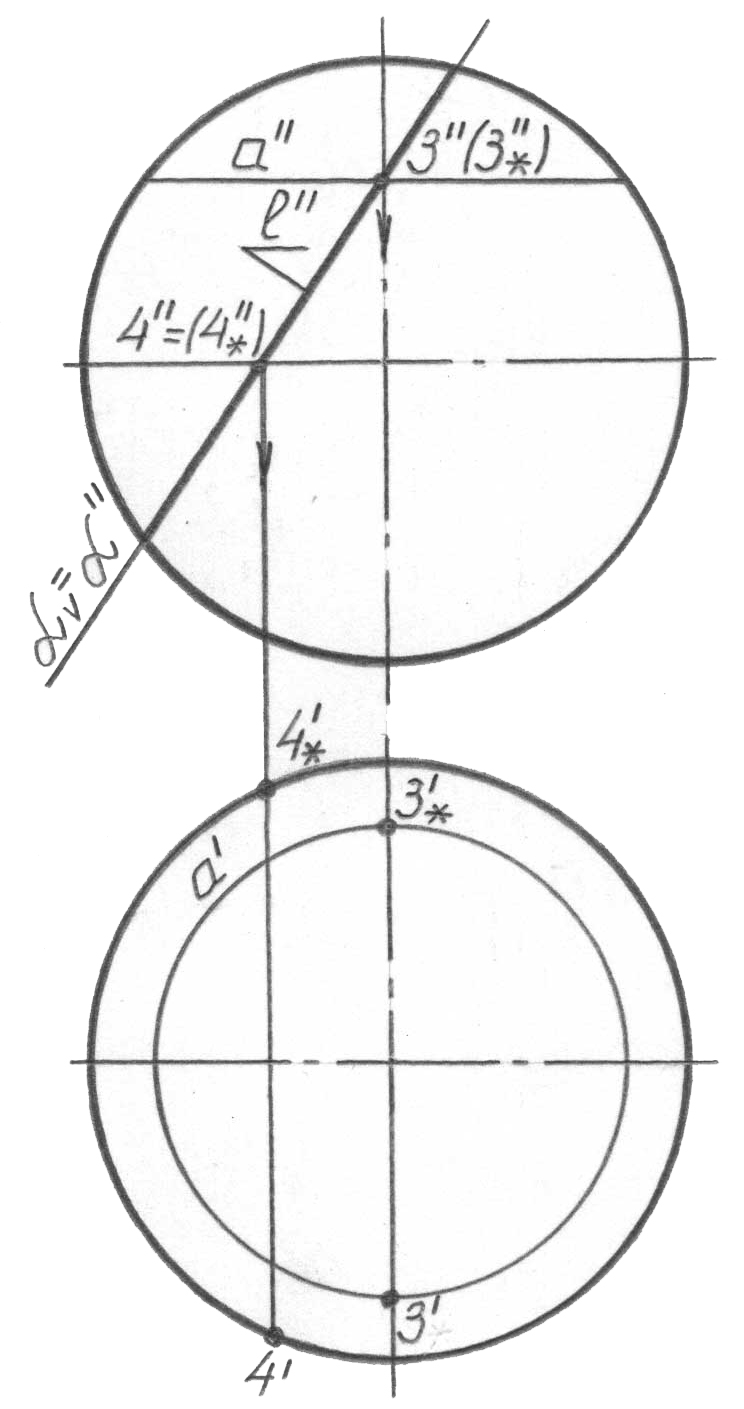
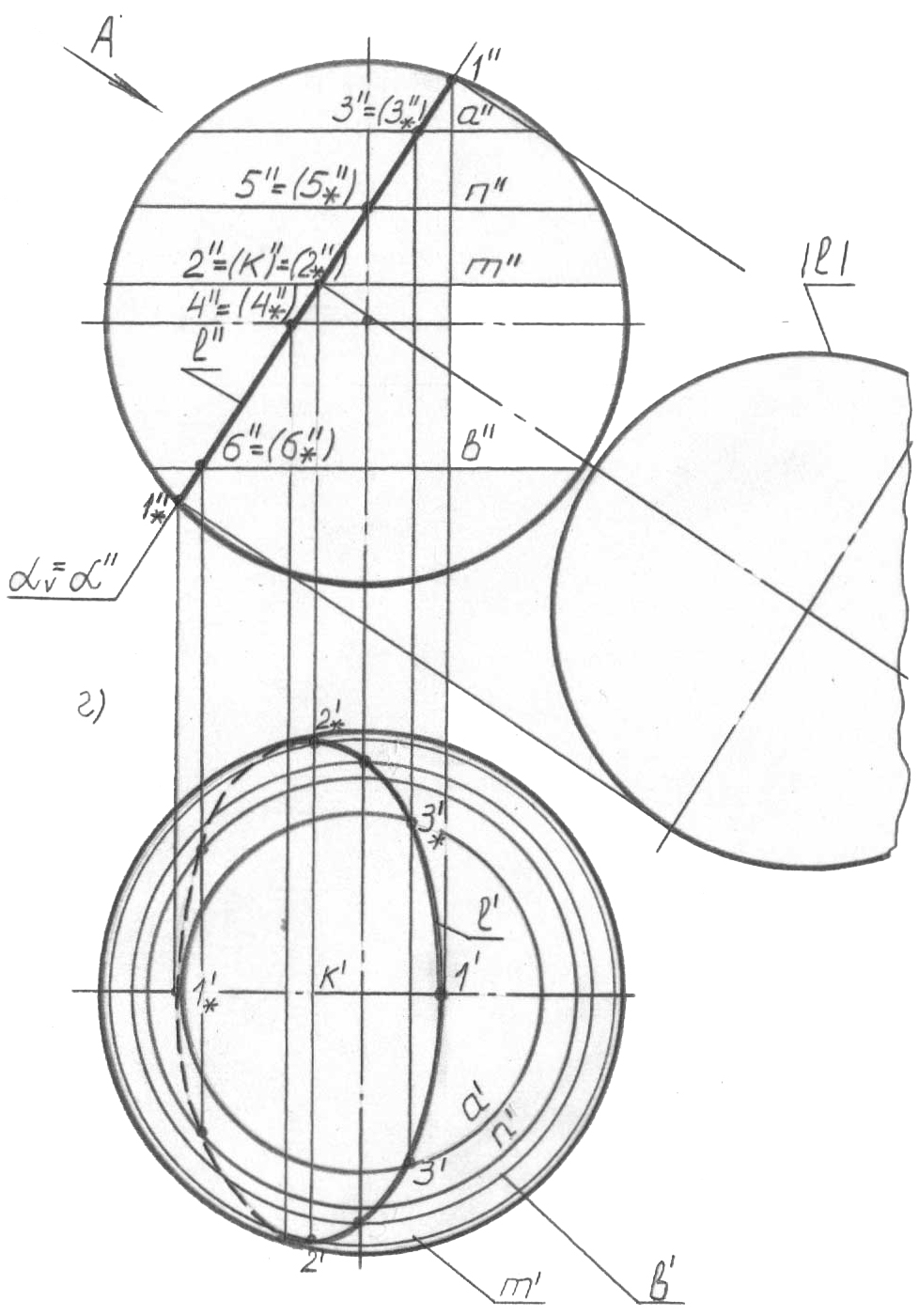
Егер 1 нүктесі (65, б-сурет) – көрінетін, ал 1* нүктесі - горизонталь проекцияда көрінбейтін болса, онда, әрине, l қисығында онда көрінушілік керіге өзгеретін нүктені анықтау қажет. Сфера үшін мұндай шекара оның экваторы және l қисығының оған тиесілі 4, 4* нүктелері (4’’ (4*’’) проекция-лары) болып табылады (65, в-сурет), олардың горизонталь проекциялары сфераның горизонталь очеркінде жатады. Екі жазықтықты сызба үшін оған тән нүктелер анықталған, және кәдімгі нүктелердің бірнеше жұбын анықтау қалады. Олардың горизонталь проекцияда орналасуы фронталь проекцияда алдын ала ерікті берілген, a, n, b параллельдері арқылы анықталады. Ал енді жеке фрагменттерді (65, а-в-сурет) бір кескінде біріктіреміз, оған кәдімгі 3, 3* (65, в-сурет) және 5, 5* және 6, 6* нүктелерін (65, г-сурет) қосамыз. Міне, қойылған есеп шешімінің нәтижесі осы.
Сфераның жазықтығымен қиылысу фигурасының |l| нақты шамасы жалпы жағдайда кешенді сызбаны түрлендірудің белгілі тәсілдерімен, мысалы, проекциялар жазықтықтарын ауыстыру тәсілімен анықталады. Қарастырыла-тын есепке қатысты, қисықтың пішіні ең қарапайым және симметриялы болған-да, қима фигурасының нақты көлемі қарапайым логикамен анықталуы мүмкін: егер қимаға жазықтығына перпендикуляр бағытта қарасақ (А стрелкасы, 65, г-сурет), 1’’-2’’ кесіндісіне тең диаметрлі шеңбер түрінде нақты көлемінде көреміз. Оны перпендикуляр, байланыс сызықтары бойынша жүргіземіз.
5.4.3 Кониктер
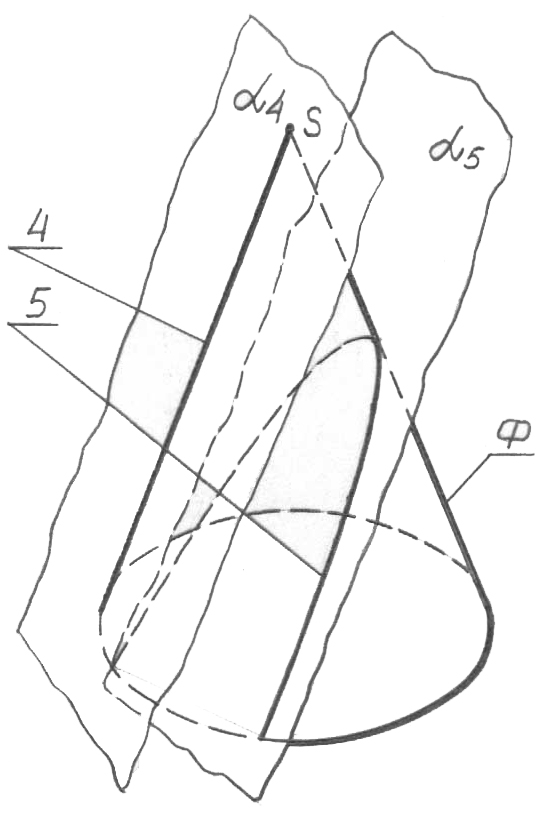
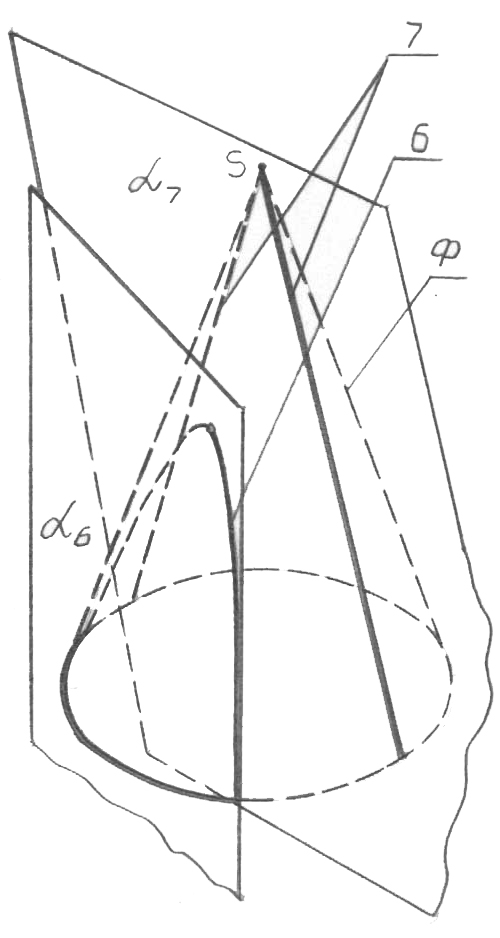
Тік дөңгелек конустың беті басқа беттердің арасында ерекше орын алады. Ол конус әр түрлі орналасқан жазықтықтармен қиылысқан кезде алынатын, екінші ретті қисықтардың: 2 - шеңбердің (66, а -сурет), 3 – эллипстің (66, а-сурет), 5 - параболаның (66, б-сурет) және 6 - гиперболаның (66, в-сурет) жиынтығын тасушы болып табылатынымен теңдессіз. 2 қиюшы жазықтығы конус осіне перпендикуляр болғанда - шеңбер; 3 жазықтығы оське
66, а-сурет
66, б-сурет
66, в-сурет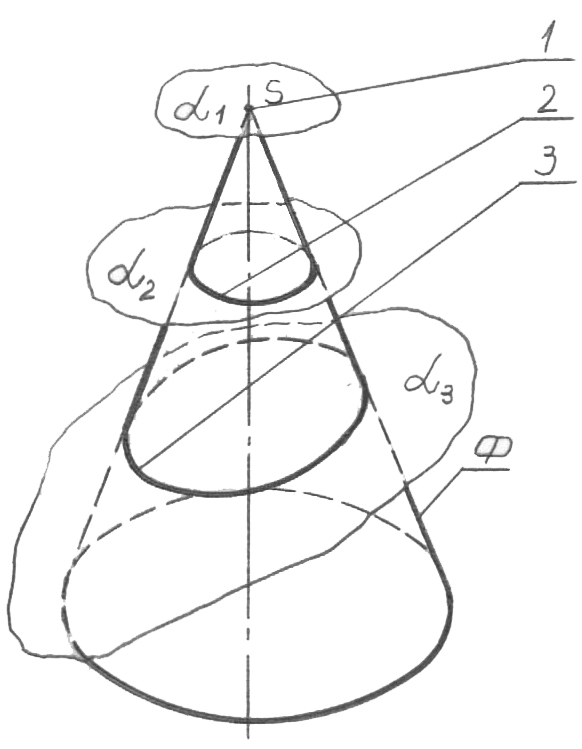


п
Рис. 66в
Өзін-өзі тексеру үшін студенттерге 5.3.3.2-тармақтың ережелерін және 63-суретті басшылыққа алып, 2-7 сызықтардың горизонталь және фронталь проекцияларын салу ұсынылады.
5.4.4 Конустың жеке орналасқан жазықтықпен қиылысуы
Е
67, а-сурет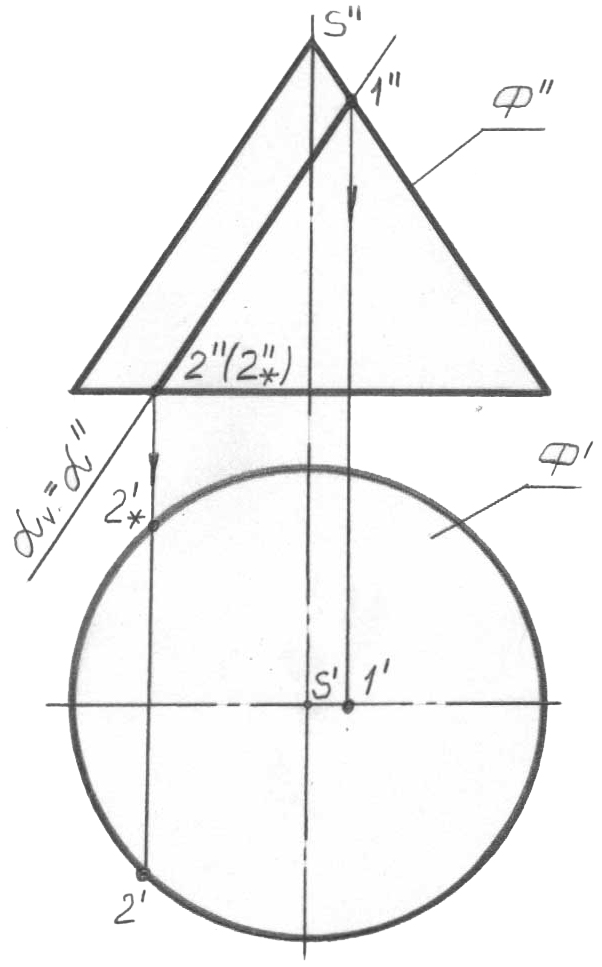
Оған тән нүктелерді анықтаймыз. 1 нүк-тесі – жоғарғы, оң; 2 және 2* нүктелері – сәй-кес түрде төменгі жақын және төменгі алыс.
1 нүктесі - бас фронталь меридианда, 2, 2* нүктелері конустың шартты экваторында (негізінде) болады, ал бұл олардың горизонталь проекцияларын тиесілігі бойынша анықтайды. Басқа тиесілі нүктелері жоқ. 3, 4, 5 нөмірлерімен белгіленген кәдімгі нүктелердің бірнеше жұбын алу ғана қалды (67, б-сурет). Олардың фронталь проекцияда орналасуы мүлдем ерікті түрде беріледі (азды-
к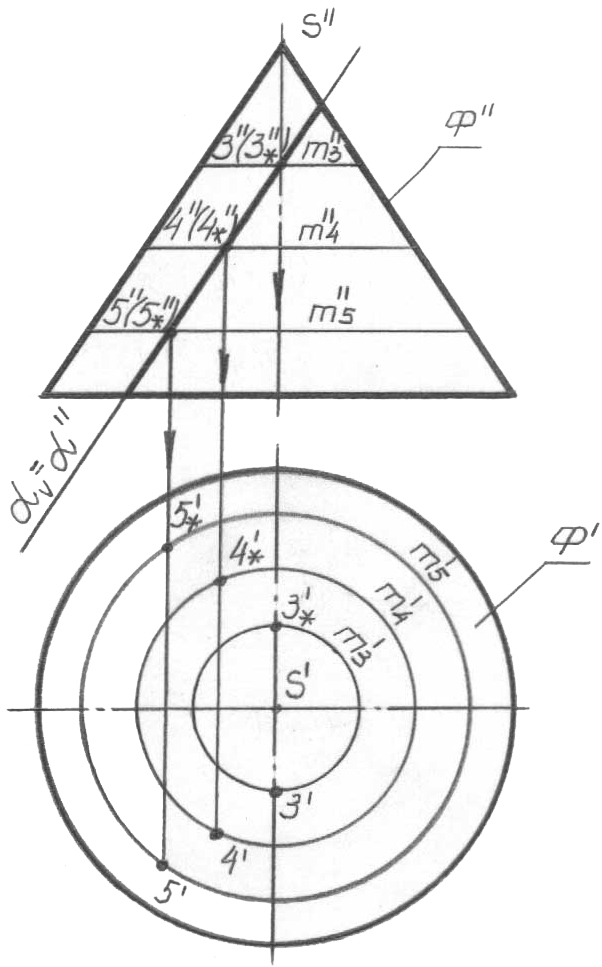 өпті
бірқалыпты болса), ал гори-зонталь
проекциялары сәйкес m3,
m4,
m5
параллельдері
арқылы анық-талады (сондай-ақ 5.3.3.2 және
63-суретті қараңыз). Кескіндерді (67, а,
б-суреттер) есепті шешу нәтижесі болып
табылатын, жалпы-лаушы кескінге (67,
в-сурет) келтіріңіз.
өпті
бірқалыпты болса), ал гори-зонталь
проекциялары сәйкес m3,
m4,
m5
параллельдері
арқылы анық-талады (сондай-ақ 5.3.3.2 және
63-суретті қараңыз). Кескіндерді (67, а,
б-суреттер) есепті шешу нәтижесі болып
табылатын, жалпы-лаушы кескінге (67,
в-сурет) келтіріңіз.
l қимасы фигурасының нақ-ты көлемін салу негізіне проек-циялар жазықтықтарын ауысты-ру әдісі салынған. Сонымен бірге келесі түрде ойлаймыз. l сызығы горизонталь проекцияда бұзылып проекцияланғандықтан, проекция-
л
67,
б-сурет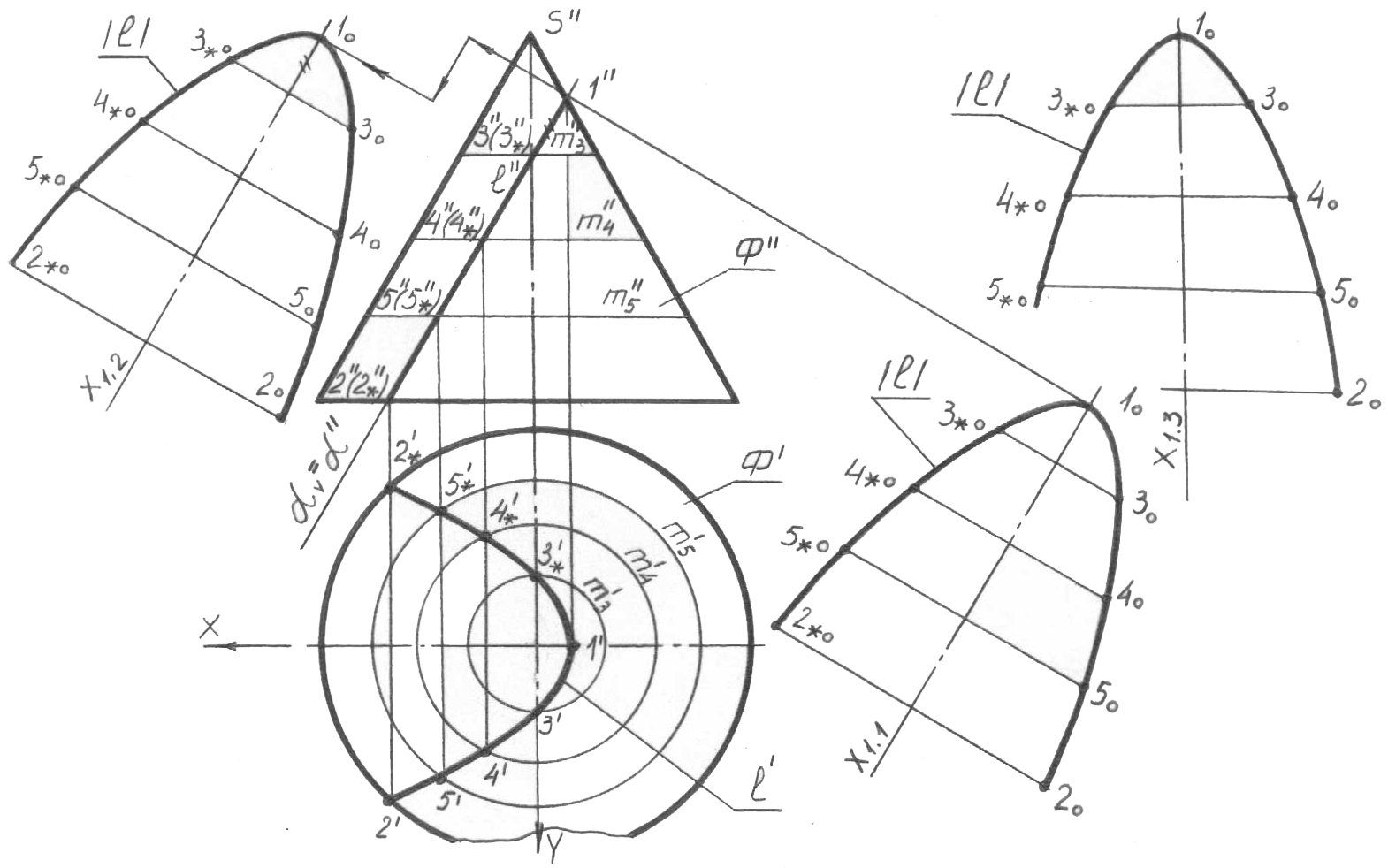 елтіріледі.
Бұл кесінділер проекциялар жазықтықтарының
ескі жүйесіндегі әрбір нүктенің Y
мәндерінің дәл өзі.
елтіріледі.
Бұл кесінділер проекциялар жазықтықтарының
ескі жүйесіндегі әрбір нүктенің Y
мәндерінің дәл өзі.
67, в-сурет
Мысалы, S’3*’ кесіндісін - x1,1 осімен оңға қарай және x1,1 осінен солға қарай, 4*’x кесіндісін өзінің байланыс сызығы бойынша және т.с.с. соңғы нүктелер жұбына дейін 2 нөмірімен қалдыру керек.
Қима фигурасының нақты көлемін жоғарыда сипатталғандай, ығысуымен (x1,2 осі бар кескінді қараңыз) және ығысуымен және бұрылуымен (x1,3 осі бар кескінді қараңыз) жалпы жағдайда проекциялық байланысты салуға болады. Соңғы екі жағдайда проекциялық байланыстардың бұзылуынан x1,2 және x1,3 осьтерінің бойында кесінді байланысының 1’’-3’’(3’’)-4’’(4*’’) сызықтары арасындағы 2’’(2*’’) нүктелеріне дейінгі ара қашықтықтар теңдігін қамтамасыз ету керек. Сонымен бірге салудың басына жаңа осьтің қай жерінде болсын орналасқан, кез-келген 10 нүктесі қабылдануы мүмкін. Қима фигурасының нақты көлемін салудың Сіз қабылдаған үш нұсқасының біреуі әрбір нақты жағдайда сызбада кескіндерді құрастыру шарттарымен анықталады. Қорытын-дысында мынаны атап өтейік: конустың горизонталь және фронталь проекция-лары арасындағы координаталық осьтердің дәстүрлі орналасуы (айтпақшы, студенттер үшін үйреншікті), ізделіп отырған |l| сызығының кескіндерін оның пішінін бұзбай, x1,1, x1,2, x1,3 осьтеріне қатысты оңға қарай ығысуына әкеліп соғушы еді және |l| сызығын салудың өзінің ыңғайлылығын кемітуші еді.
5.4.5 Пирамиданың жеке орналасқан жазықтықпен қиылысуы
П
68-сурет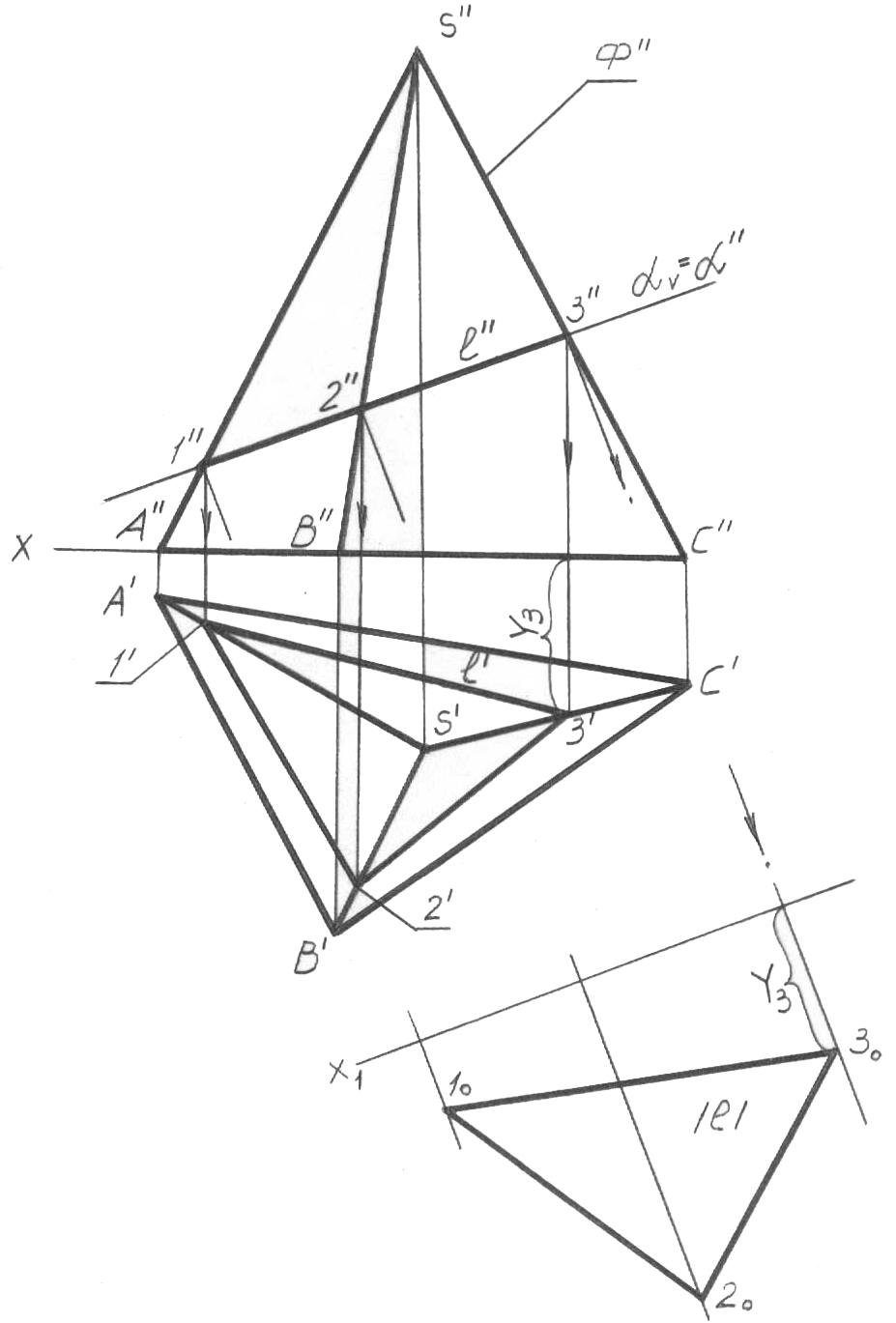
үшін де, жазықтығы үшін де ортақ болып табылатын, ізделіп отырған 1, 2, 3 нүктелері, әрбір қыр проекциясының жазықтығының V = ’’ із-проекция-сымен қиылысуының 1’’, 2’’, 3’’ нүктелерін білдіретін болады.
1’, 2’, 3’ нүктелерінің горизонталь проекциялары олардың әрбір қырға тиесілігі бойынша анықталады. жазықтығы пирамиданың АВС негізіне параллель емес болғандықтан, үшбұрыштың 1’2’3’ қабырғаларының біреуі де A’B’C’ негізінің сәйкес қабырғаларына параллель болмау керек.
Қиманың пішіні симметриялы емес болғандықтан, қима фигурасының нақты көлемін салу үшін бастапқы V/H жүйесінде x осінің орналасуын дәстүрлі түрде, яғни пирамиданың негізімен сәйкес келетіндей етіп береміз. Оларда 10, 20, 30 нүктелерінің орналасуын анықтау үшін, жазықтығына және проекция-лық байланыс сызығына параллель (1’’, 2’’, 3’’ нүктелерінен V = ’’ перпенди-куляр) х1 осін жүргіземіз. 3 нүктесінің байланыс сызығы бойынша қимада x осі-нен 3 нүктесінің 3’ горизонталь проекциясына дейін алынған, Y3 ара қашықты-ғын қалдырамыз. Нәтижесінде ізделіп отырған үшбұрыштың шынайы пішінін анықтайтын, 30, 20, 10 нүктелерін алып, 2 және 1 нүктелермен де солай істейміз.
5.4.6 Призманың жеке орналасқан жазықтықпен қиылысуы
6
69-сурет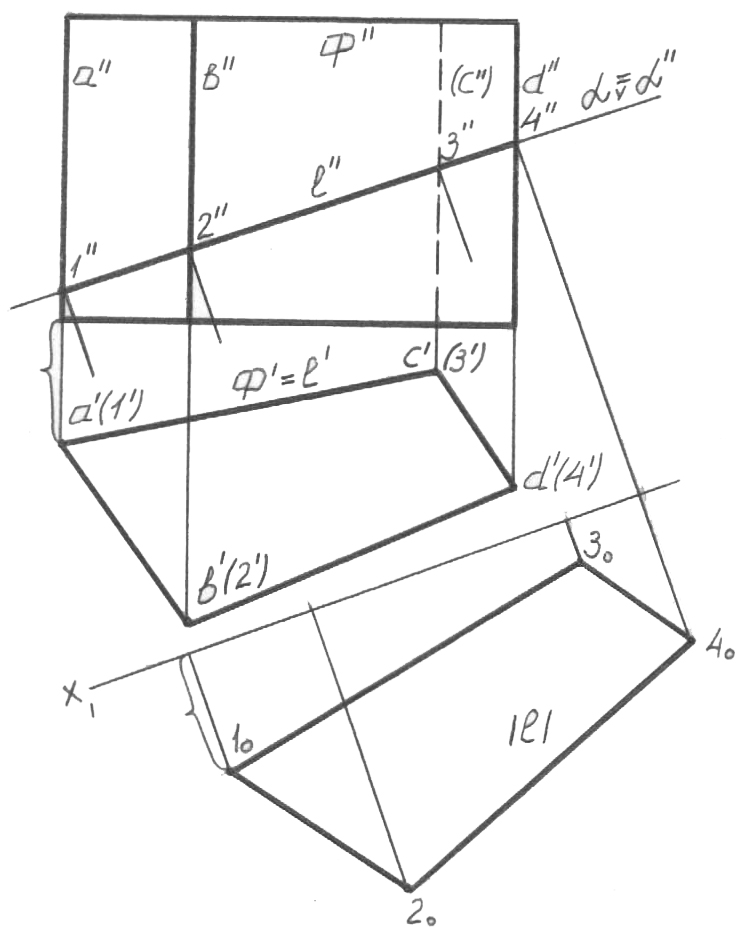
5.4.7 Цилиндрдің жеке орналасқан жазықтықпен қиылысуы
7
70-сурет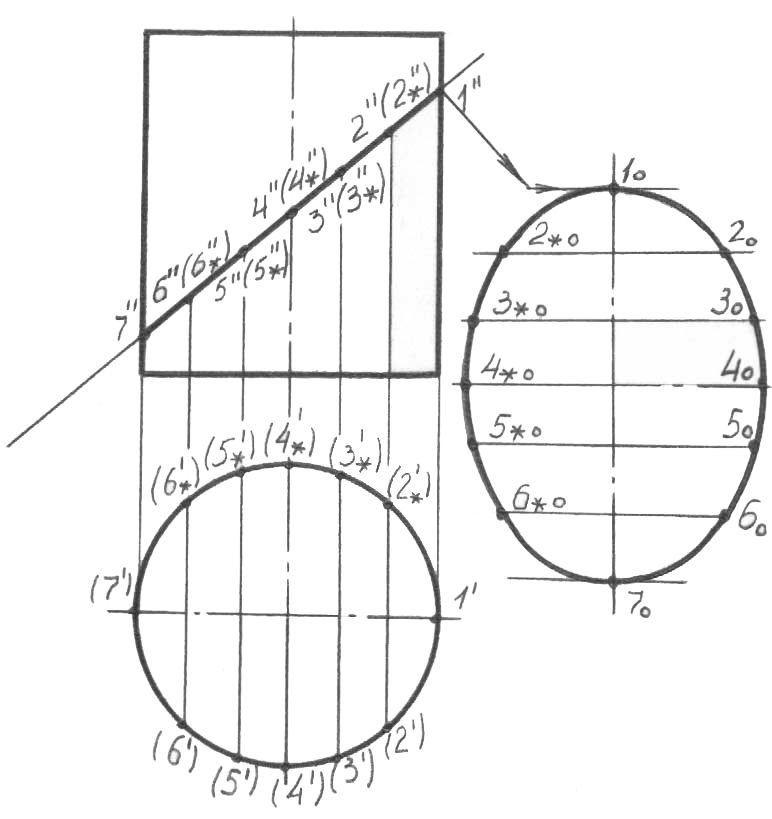
циясы шеңберді білдіреді.
Қима фигурасының нақты көлемі ығыстырумен және бұрумен салынған эллипсті білдіреді. Оны салу тәртібі 67-суретке ұқсас. 20, 30 және т.б. нүкте-лер-дің Y координатасының ағымдағы мәндері фигуралы жақшалармен берілген.
Қарастырылған тақырыптама бірнеше элементар геометриялық пішіндер-дің жиынтығын білдіретін, кез-келген пішін үйлесімді заттардың қимасы фигурасының проекциялары мен нақты шамасын жүзеге асыруға мүмкіндік береді.
5.5 Беттердің қиылысуы
5.5.1 Беттердің қиылысу сызығын салудың жалпы алгоритмі
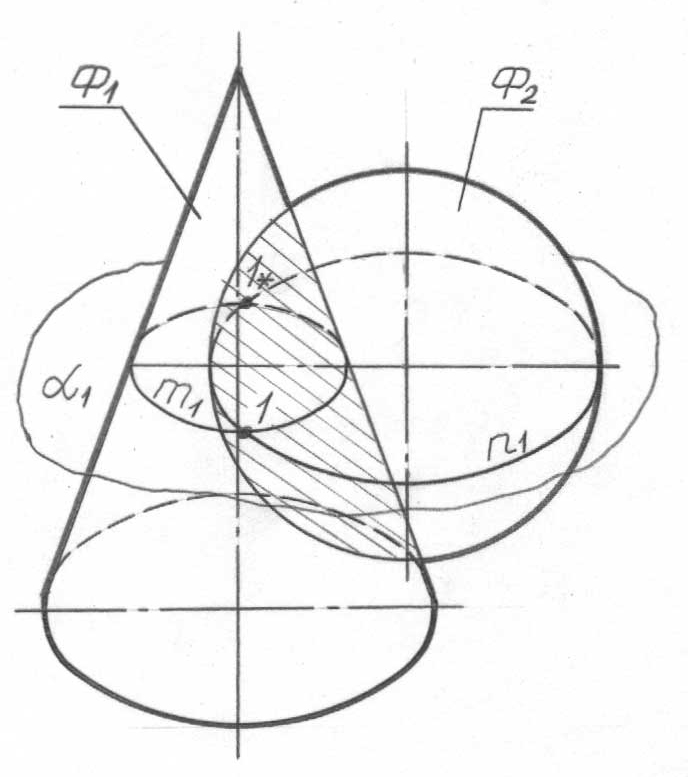
Ф1 және Ф2 беттерінің қиылысу сызығын салу үшін (71-сурет) қажет:
Б
 ерілген
беттерді қосым-ша
геометриялық элемент – қосымшамен
(α1)
қиып өту.
ерілген
беттерді қосым-ша
геометриялық элемент – қосымшамен
(α1)
қиып өту.Қосымшаның (α1) әрбір бетпен жеке қиылысу сызықта-рын (m1 және n1) салу.
Алынған сызықтардың (m1 және n1) қиылысу нүктелерін (1 және 1*) табу.
71-сурет
Осы алгоритмді қажетті есе рет қайталау (71-суретте бұл көрсетілмеген).
Алынған нүктелерді (1, 1*, 2, 2* және т.б.) өз араларында қажетті тізбектілікте қосу. Салу ретін символдық жазу келесі түрде болады.
α1 ∩ Ф1 = m1; α1 ∩ Ф2 = n1; m1 ∩ n1 = 1, 1* – бірінші қадам.
α2 ∩ Ф1 = m2; α2 ∩ Ф2 = n2; m2 ∩ n2 = 2, 2* – екінші қадам және т.с.с.
і) αk∩ Ф1 = mk; αk ∩ Ф2 = nk; mk ∩ nk = k, k* – соңғы қадам.
l = {1, 1*, 2, 2*, ... k, k*}.
Беттердің қиылысуына арналған кез-келген есепті шешуді едәуір жеңіл-дету және дәлдігін қамтамасыз ету үшін алгоритмнің әрбір қадамының ішінде бар салынатын элементтерге сол және бір индексті тағайындау ұсынылады, яғни, мысалы, 5 индексімен қосымшаны, m5 және n5 сызықтарын береді, олардың қиылысуы өздерінің ерекше белгілерімен 5 нөмірлі (5*, 50, 5., 5∆ және т.с.с.) нүктелерді береді.
5.5.2 Жалпы ескертулер
Жалпы жағдайда қосымшалар ретінде жалпы орналасқан жазықтық-тар, жеке орналасқан жазықтықтар, концентрлік немесе эксцентрлік сфералар, цилиндрлер және нақты графикалық есепке байланысты т.б.
Қосымша m және n сызықтары ең қарапайым (шеңберлер, түзулер, түзулер жиынтығы) болатындай, сондай (түрі бойынша) және осылай (орналасуы бойынша) болып таңдалу керек.
Ізделіп отырған l сызығының 1, 2 және т.б. нүктелері қиылысатын беттер проекцияларының өзара салыну ауданының шегінде орналасу керек (71-суреттің күңгірттелген аймағы).
Салуды "оған тән" деп аталатын нүктелерден: жоғарғы, төменгі, сол, оң, жақын, алыс, көрінушілік аймақтары шекараларынан және т.с.с. бастау керек. Егер ізделіп отырған сызықтар сипатын бір мағыналы анықтау үшін оған тән нүктелер жеткіліксіз болса, "кәдімгі" деп алатын нүктелерді табу қажет.
Егер қиылысатын беттердің проекциялардың қандай да бір жазықты-ғына параллель, жалпы симметрия жазықтығы болса, онда олардың очерктерінің қиылысуы оған тән екі нүктені береді, ал қалған нүктелер (соның ішінде оған тән де) бір-бірінің жармасында болады.
Қиылысу сызығының реті қиылысатын беттер реттерінің көбейтінді-сіне тең.
Нүктелердің көрінушілік-көрінбеушілік мәселелері және олардың қосылу тізбектіліктері әрбір есеп үшін жеке шешіледі.
5.5.3 Жазық ортаңғы сызықтар әдісі
71-суретте көрсетілген алгоритмнің мәнін көрнекті көрсетуден, тікелей осы беттердің екі жазықтықты сызбада қиылысу сызығын салуға ауысамыз (72-сурет). Есеп шартының формулаландырылған жазбасы келесідей түрде болады:
Ф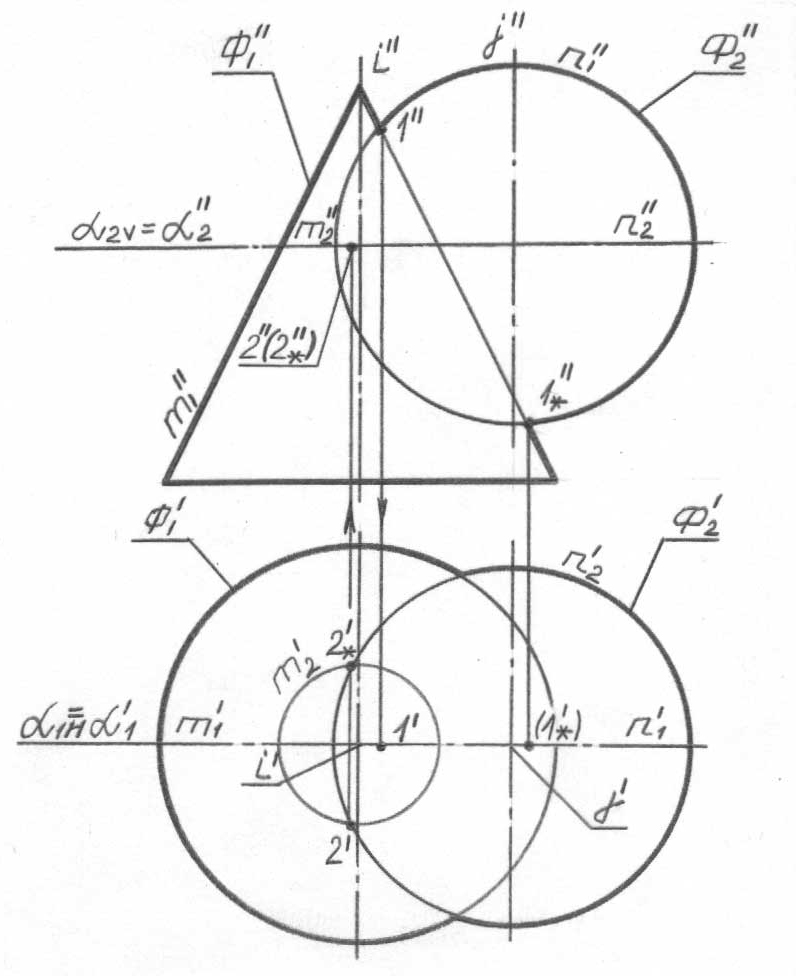 1,
Ф2; Ф1 ∩ Ф2 = l?
1,
Ф2; Ф1 ∩ Ф2 = l?
72, а-сурет
Есепті талдау және шешу.
Екінші ретті екі айналу беті қиылысады, осыдан, ізделіп отырған l сызығы төртінші ретті болады.
Қиылысу түрі – "бұранда" (алмасатын қиылысу) болғандықтан, онда l сызығы біреу болады.
Беттердің проекциялардың фронталь жазықтығына параллель, α1 симметриясының жалпы жазықтығы бар (72, а-сурет), ендеше олардың Ф1'' және Ф2'' фронталь очерктерінің қиылысуы оған тән екі нүктені береді: 1'' – жоғарғы және 1*'' – төменгі. Айтпақшы, бірінші қосымша ретінде α1 жазықтығын пайдаланудың тура сол нәтижені беретінін байқаймыз, өйткені m1'' және n1'' сызықтары беттердің фронталь очеркінен басқа ештеңе емес.
Осы есепте келесі салулар үшін қосымшалар ретінде α2, α3 және т.б. горизонталь жазықтықтарды қабылдау мақсатқа сәйкес болады, өйткені олардың беттердің әрқайсысымен қиылысу сызықтары (72, а, б-суретті қараңыз) ең қарапайым (шеңберлер) болып табылады.
Проекциялардың горизонталь жазықтығы үшін ізделіп отырған l сызығының көрінушілік аймағының шекарасы сфераның экваторы болып табылады, сондықтан Ф2 сферасының экваторы арқылы өткізіл-ген жазықтық – α2 қосымшасы, алгоритмнің екінші қадамында проекциялардың горизонталь жазықтығы үшін көрінушілік аймағы-ның шекаралары болып табылатын, экваторға тиесілі 2 және 2* нүктелерін береді. Осы нүктелер ең сол нүктелер болып табылады.
Проекциялардың фронталь жазықтығы үшін көрінушілік шекаралары қиылысатын беттердің бас фронталь меридиандары және оған тиесілі 1 және 1* болып табылады. Проекциялардың фронталь жазықтығына параллель, α1 симметриясының жалпы жазықтығының бар болуы есебінен, V жазықтығындағы ізделіп отырған l сызығының көрінбейтін бөлігі қисықтың көрінетін бөлігімен толығымен жабылады (бұл туралы 2(2*) нүктелерінің екі рет белгіленуі куәландырады) және т.б. Қарастырылатын есепте басқа оған тән нүктелер жоқ.
72, б-сурет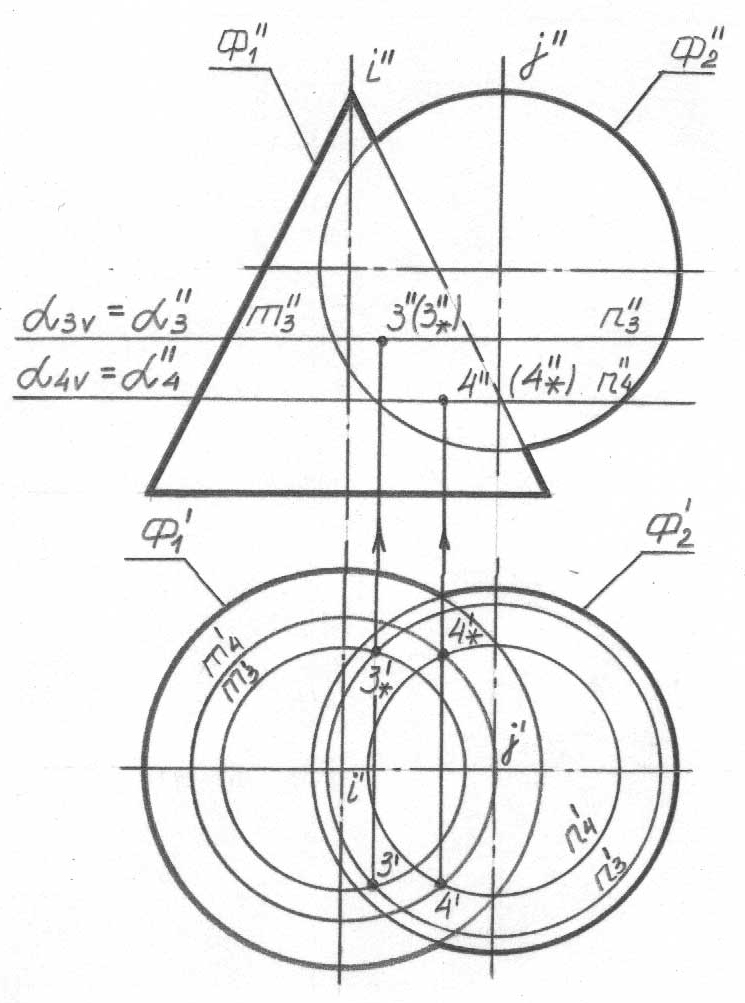
Сөйтіп, беттердің қиылысу сызықтарын салу келесіге келтіріледі.
Біріншіден, (72, а-сурет) беттердің i және j осьтері арқылы проекция-лардың фронталь жазықтығына параллель, α1 жазықтығын жүргіземіз. Проек-циялардың горизонталь жазықтығында – бұл х осіне параллель, α1Н = α1' із-проекциясы. Фронталь проекциядан Ф1'' және Ф2'' очерктері қиылысуының 1'' және 1*'' нүктелерін қарастырамыз. Алынған нүктелерді олардың көрінушілігін есепке алумен, α1 жазықтығының α1Н = α1' горизонталь із-проекциясына түсіреміз (1' нүктесі – көрінетін, 1*' нүктесі – көрінбейтін). Алгоритмнің бірінші қадамын мына түрде жазамыз:
1) α1 || V; α1 i, j; α1 ∩ Ф1 = m1; α1 ∩ Ф2 = n1; m1 ∩ n1 = 1, 1*.
1 нүктесі – жоғарғы, 1* нүктесі – төменгі.
Алгоритмнің кеңістік үшін жазылатынын, ал проекциялардың әрбір жазықтығы үшін нүктелердің проекцияларын және l сызығын салу әрбір салу элементін міндетті белгілеумен жүргізіледі.
Екіншіден, Ф2 сфераның экваторы арқылы проекциялардың горизонталь жазықтығына параллель, α2 жазықтық-қосымшаны жүргіземіз (α2V = α2'' қараңыз). Фронталь проекцияның m2 және n2 параллельдері айырылмайды, өйткені олардың m2'' және n2'' проекциялары бір-біріне жартылай салынады. Сондықтан сәйкес радиусты шеңберлер және олардың қиылысуының 2' және 2*' нүктелері сияқты, олардың m2' және n2' горизонталь проекцияларын табамыз. Осы нүктелердің 2'' және 2*'' фронталь проекцияларын α2 жазықтығының α2V = α2'' із-проекциясында проекциялық байланыс нүктелері бойынша табамыз. Алгоритмнің екінші қадамын жазамыз.
2) α2 || Н; α2 ∩ Ф1 = m2; α2 ∩ Ф2 = n2; m2 ∩ n2 = 2, 2*.
Екі нүкте де – Н жазықтығы үшін көрінушілік шекаралары.
Үшіншіден, Н жазықтығына параллель, α3 жазықтығын ерікті жүргіземіз. Екінші қадамға ұқсас, осы жазықтықтың әрбір бетпен қиылысу сызықтарының m3' және n3' горизонталь проекцияларын және 3 және 3* нүктелерінің 3' және 3*' горизонталь проекцияларын, ал содан кейін α3V = α3'' із-проекциясында – осы нүктелердің 3'' және 3*'' фронталь проекцияларын табамыз. Алгоритмнің үшінші қадамын табамыз.
3) α3 || Н; α3 ∩ Ф1 = m3; α3 ∩ Ф2 = n3; m3 ∩ n3 = 3, 3* - кәдімгі нүктелер.
Осыған ұқсас түрде 4 нөмірімен мына нүктелерді алуға болады:
4) α4 || Н; α4 ∩ Ф1 = m4; α4 ∩ Ф2 = n4; m4 ∩ n4 = 4, 4* - кәдімгі нүктелер және қарастырылатын есеп үшін осы жеткілікті.
Алдын ала 72, а және 72, б-суреттерді бір кескінге біріктіріп (72, в-сурет), нүктелердің өз араларында қосылу тәртібін анықтаймыз. Ізделіп отырған l қисығы тұйықталған болып табылатындықтан, оны салуды кез-келген нүкте-ден және кез-келген бағытта бастауға болады, мысалы 1, 2, 3, 4, 1*, 4*, 3*, 2*, 1. Алгоритмнің қорытынды тізбегі мына түрде жазылуы мүмкін:
l = {1, 2, 3, 4, 1*, 4*, 3*, 2*, 1}
Есепті ресімдеу мысалы 72, в-суретте берілген.
72, в-сурет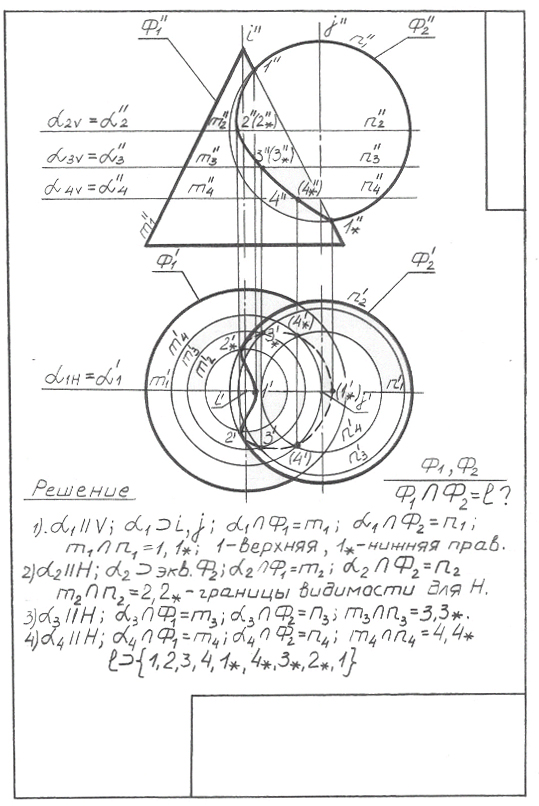
5.5.4 Концентрлік сфералар әдісі
Осы әдістің қолданылуы осьтес ьеттердің қиылысуы туралы теоремаға негізделген. Жалпы айналу осі бар беттер осьтес деп аталады. Теореманың мәні келесіге келтіріледі: екі осьтес айналу беттері қиылысуының l сызығы шеңбер (параллель) болып табылады, оның жалпы айналу осіне параллель l’’ проекциясы дегеніміз түзу сызық, ал жалпы айналу осіне перпендикуляр жазықтыққа дегеніміз – нақты көлемнің l’ шеңбері (73, а-сурет). Бұл принцип-тік ереже кез-келген осьтес қиылысатын беттердің кез-келген кеңістіктік орны үшін дұрыс болады (73, а және 73, б-суреттерді салыстырыңыз). Қорытынды-сында кез-келген түрде қиылысатын екі сфера ылғи да осьтес, сондықтан олардың центрлері арқылы өтетін түзу ылғи да олардың жалпы айналу осі болып табылады.
73, а-сурет
73, б-сурет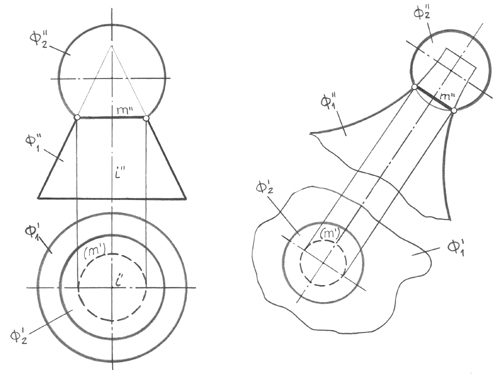
Тік дөңгелек конус және дөңгелек цилиндр мысалында концентрлік сфералар әдісін пайдалану арқылы беттердің қиылысу сызықтарын салу есебін қарастырамыз. Түсінуді ықшамдау үшін 74-суретте есептің кезеңмен шешілуі берілген. Алдын ала осы әдісті қолдану шарттарын тұжырымдаймыз. Олар - үшеу. Біріншіден, қиылысатын беттер айналу беттері болуы керек. Екіншіден, беттердің осьтері қиылысу керек. Үшіншіден, беттердің проекциялар жазық-тықтарының біреуіне параллель, жалпы симметрия жазықтығы болу керек. Бұл шарттар бір мезгілде орындалу керек. Концентрлік сфералар әдісін қолдану-дың керекті нәтижені ең қарапайым жолмен беретін, кез-келген басқа қосымшаларды пайдалануды жоққа шығармайды.
Концентрлік сфералар әдісінің кейбір артықшылықтары мынадан тұрады: ол беттердің бірдей проекцияда қиылысуының ізделіп отырған сызығын алуға мүмкіндік береді (проекциялардың басқа жазықтықтарында салмай-ақ). Алайда, оқу процесінде де, инженерлік практикада да бұл артықшылықты арттырудың керегі жоқ.
74, а-сурет
74, б-сурет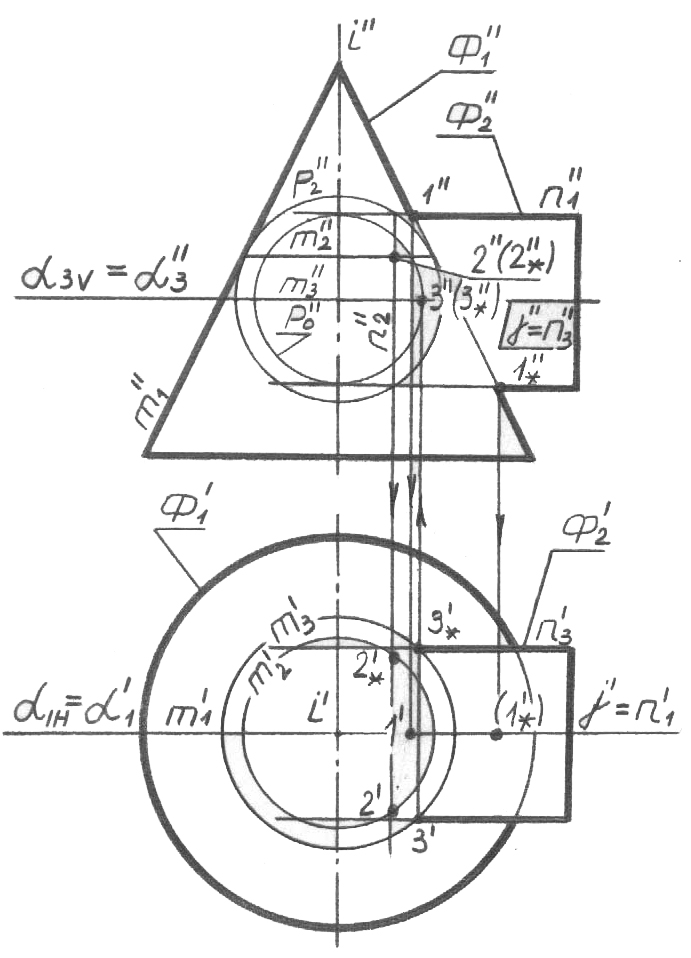
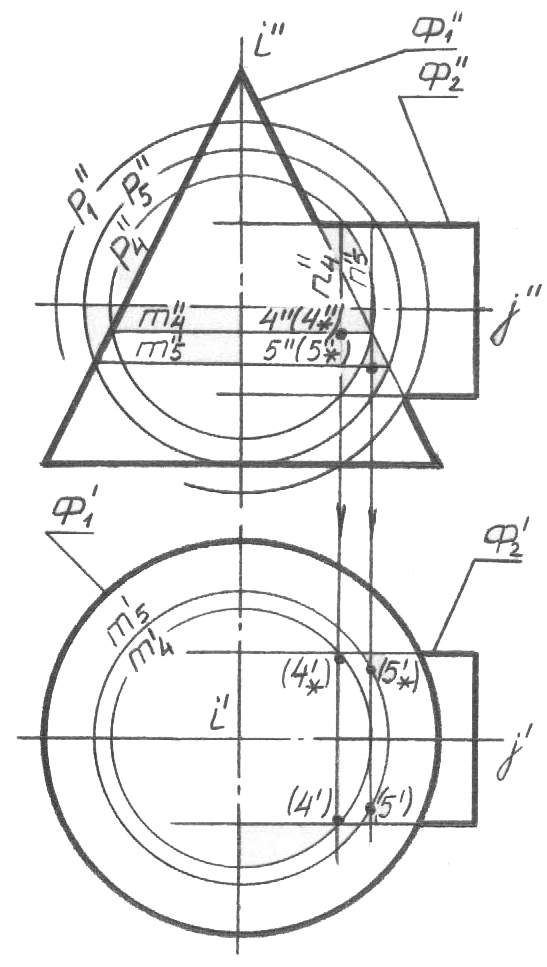
74, в-сурет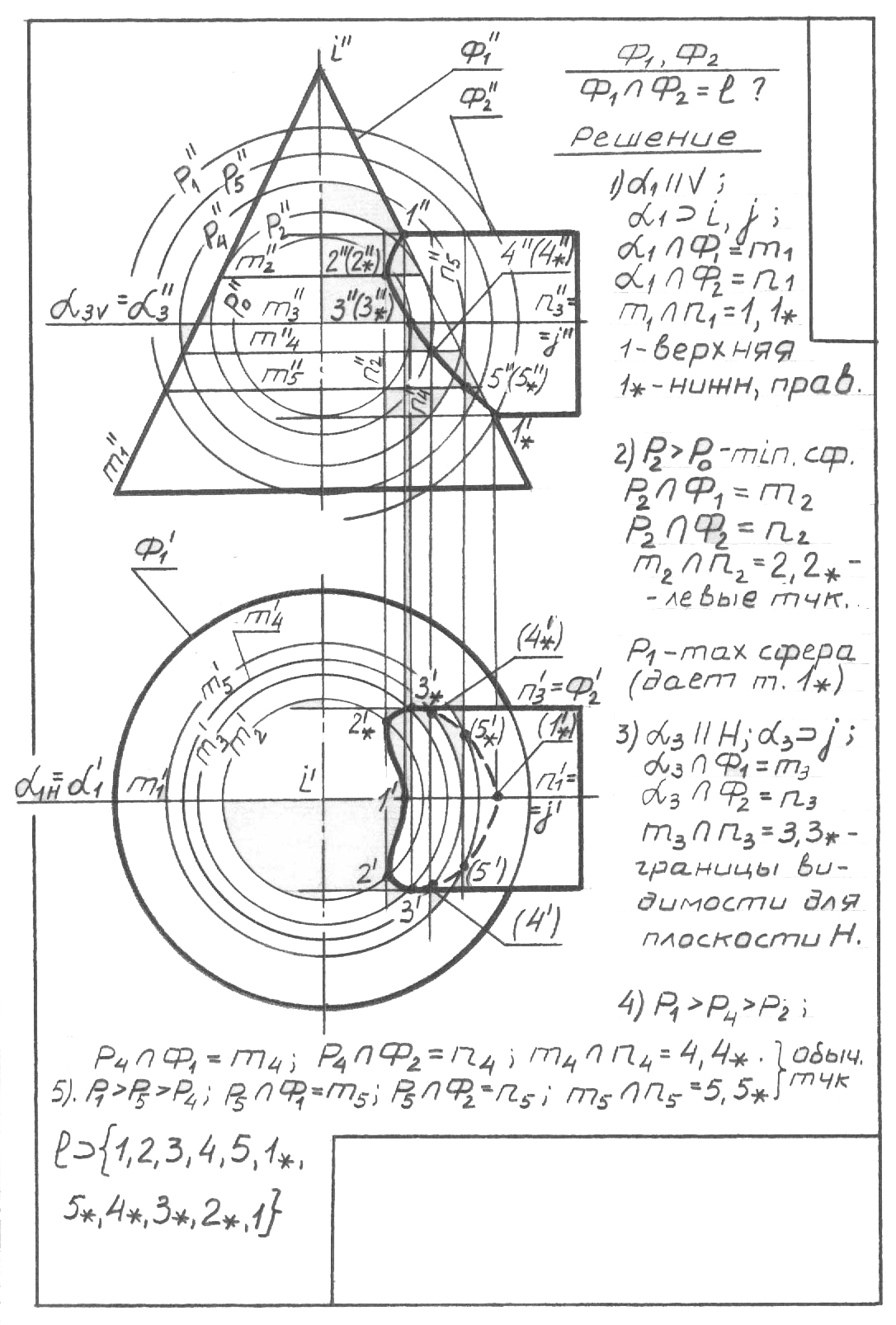
Сфералық қосымшалар беттер осьтерінің қиылысу нүктесінен жүргізілу керек, өйткені тек осы жағдадйда ғана олар (қосымшалар) қиылысатын беттер-дің әрқайсысымен осьтес болып шығады. Минимум қосымша ретінде осьтер-дің (i және j) қиылысу нүктесінен әрбір бетке жеке салынған, сфералардың ең үлкені (Р2, 74, а-сурет) қабылдану керек. Бұл салынған сфералардың ең кішісі-нің (Р0) басқа бетпен (Ф1) қиылысу (немесе жанасу) сызығын бермейтінімен байланысты және осыдан, қиылысатын беттер үшін ортақ нүкте бермейді. Максимум қосымша ретінде сфера (Р1, 74, б-сурет) қабылданады, оның радиусы i және j осьтерінің қиылысу нүктесінен Ф1 және Ф2 беттерінің очерктері қиылы-суының аса қашықтатылған нүктесіне дейінгі (1*, 74, а-сурет) ара қашықтыққа тең. Қалған сфералық қосымшалар минимумнан артық және максимумнан кем болу керек.
Есепті шешу және талдау.
Қарастырылатын мысал үшін алдыңғы есептің 1-3 тармақтары (72-сурет) бір-біріне дұрыс.
Проекциялардың фронталь жазықтығында Р минимум қосымшасын анықтау үшін (74, а-сурет), сәйкес түрде Ф2 және Ф1 беттеріне (Ф2'' және Ф1'' проекцияларына) салынған, Р0 және Р2 сфераларын (Р0'' және Р2'' проекцияларын) жүргіземіз. Минимум қосымша ретінде Ф1 кону-сының бетімен (Ф1'' проекциясы) қиылысудың m0 сызығын бермейтні, ретінде, Р0 (Р0'' проекциясы) қайтарып, Р2 сферасын (Р2'' проекциясы) қабылдаймыз. Р2 сферасының (Р2'' проекциясы) Ф1 конусымен (Ф1'' проекциясы) жанасу нүктесі арқылы оның Ф1 конусымен (Ф1'' проек-циясы) жанасатын m2 (m2'' проекциясы) жүргіземіз (жанасу дегеніміз – қиылысудың жеке жағдайы екенін есепке салайық), ал Р2-нің (Р2'' проекциясы) Ф2 цилиндрімен (Ф2'' проекциясы) қиылысу нүктелері арқылы Р2 қосымшаның Ф2 цилиндрімен қиылысуының n2 сызығын (n2'' проекциясы) жүргіземіз. m2'' және n2''2'' сызықтарының (кеңістікте – шеңберлердің) қиылысуының 2*'' нүктелерін табамыз. m2 параллелі-нің m2' горизонталь проекциясын табамыз және байланыс сызығы бойынша оған 2', 2*' нүктелерін түсіреміз. Алгоритмнің екінші қадамын жазамыз.
2. Р2 > P0 - минимум сфера. Р2 ∩ Ф1 = m2; Р2 ∩ Ф2 = n2; m2 ∩ n2 = 2, 2* - сол нүктелер. Максимум қосымша ретінде бұрын алынған 1* нүктесі (1*'' проекция-сы) арқылы өтетін, Р1 сферасын (74, б-сурет) қабылдаймыз. Қалған сфералық қосымшалардың радиусы Р2-ден артық және Р1-ден кем.
Ізделіп отырған l горизонталь проекциясының көрінушілік аймағының шекарасын анықтау үшін Ф2 цилиндрінің шартты экваторы арқылы (j осі арқылы) α3 деңгейінің горизонталь жазықтығын (α3V = α3'' із-проекциясы) жүргіземіз. Бұл α3 жазықтығы Ф1 конусын m3 шеңбері (m3'' проекциясы) бойымен, ал Ф2 цилиндрі тікбұрыш бойынша қиып өтеді, оның фронталь проекциясы дегеніміз n3'' түзуі, ал n3' горизон-таль проекциясы Ф2 цилиндрінің Ф2' горизонталь очеркімен сәйкес келеді. m3 және n3 сызықтарының m3' және n3' горизонталь проекция-лары қиылысып, 3 және 3* нүктелерін (3' және 3*' проекциялары) береді. Осы нүктелердің 3'' және 3*'' фронталь проекциялары проек-циялық байланыс сызықтары бойынша α3 жазықтығының α3V = α3'' із-проекциясында болады. Алгоритмнің үшінші қадамын жазамыз.
3. α3 || Н; α3 j; α3 ∩ Ф1 = m3; α3 ∩ Ф2 = n3; m3 ∩ n3 = 3, 3*. – бір мезгілде жақын және алыс нүктелер болып табылатын, проекциялардың горизонталь жазықтығы үшін көрінушілік шекаралары.
Осымен оған тән нүктелер аяқталады және кәдімгі нүктелерді салуға өту керек.
Р4 сфералық қосымшасын, Р2 үлкен және Р1 кіші (Р4'' проекциясы) саламыз. Р4 қосымшаның конус пен цилиндрдің беттерімен қиылы-суының m4 және n4 сызықтарының m4'' және n4'' фронталь проекция-ларын және осы сызықтардың қиылысуының m4'' және n4'' нүктелерін табамыз. m4 параллелінің m4' горизонталь проекциясын және онда байланыс желісі бойынша – ізделіп отырған нүктелердің 4', 4*' горизонталь проекцияларын саламыз. Алгоритмнің төртінші қадамын жазамыз.
4. Р1 > P4 > P2; Р4 ∩ Ф1 = m4; Р4 ∩ Ф2 = n4; m4 ∩ n4 = 4, 4*.
Алгоритмнің бесінші қадамы осыған ұқсас түрде шешіледі және жазылады.
5. Р1 > P5 > P2; Р5 ∩ Ф1 = m5; Р5 ∩ Ф2 = n5; m5 ∩ n5 = 5, 5*.
және алгоритмнің қорытынды тізбегі
l {1,2,3,4,5,1*,5*,4*,3*,2*,1}
74, а және 74, б-суреттерді бір кескінде біріктіріп, онда осы тапсырманы ресімдеу мысалы берілген, 74, в-сурет түріндегі есептің түпкілікті шешімін алыңыз.
