
3.4 Жазықтықтағы түзу және нүкте
Түзу мен нүктенің жазықтыққа тиесілігіне арналған есептер жалпы жағдайда екі типтік есепке келтіріледі.
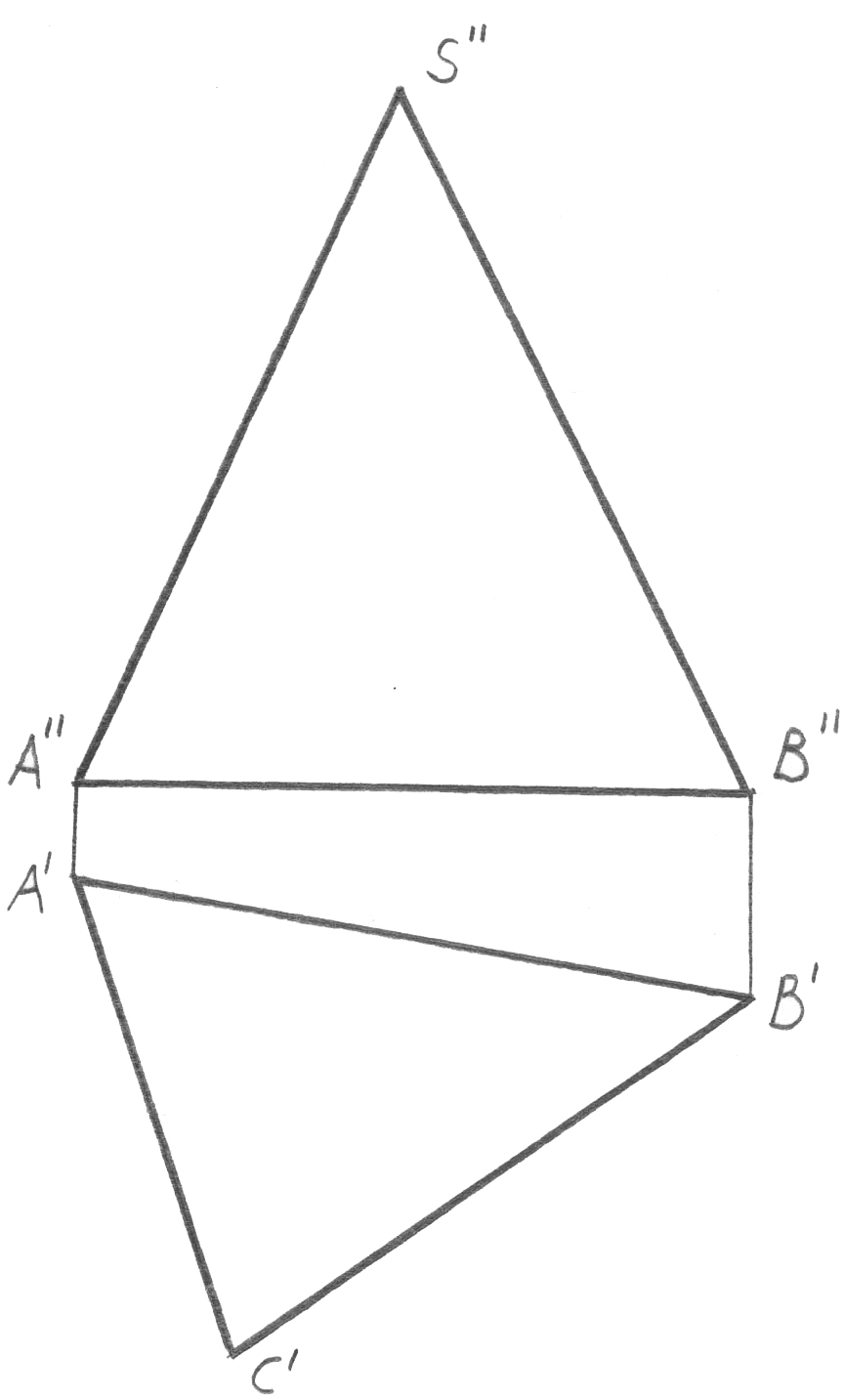
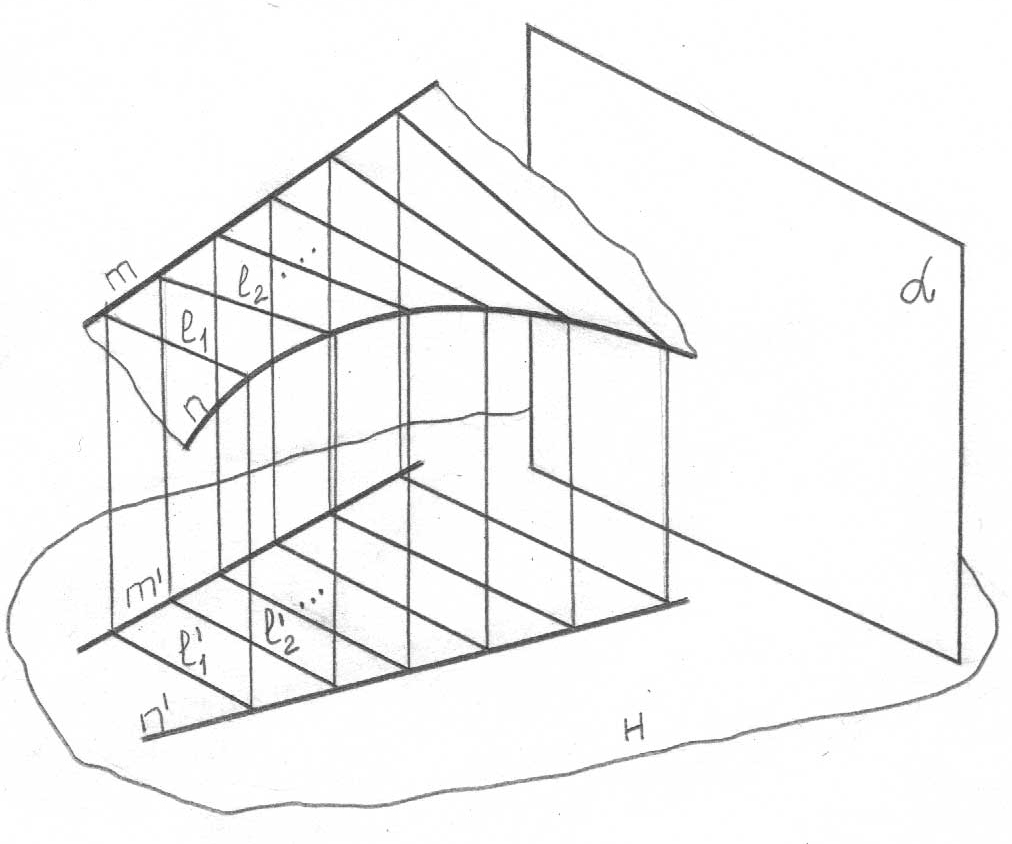
Бірінші типтік есеп. жазықтығы кез-келген түрде, мысалы, екі парал-лель түзумен l || m (немесе олардың АВ, СD кесінділерімен) берілген, 29, а-сурет. Осы жазықтыққа тиесілі, кез-келген n түзуін жүргіземіз. Келесі түрде ой жүгіртеміз. l түзуі өзінің барлық нүктелерімен (өйткені ол осы жазықтықты береді), соның ішінде 1 ерікті нүктесімен (қараңыз 1’’ A’’B’’ және 1’ A’B’) жазықтығына тиесілі болады. Осыған ұқсас түрде 2 нүктесінің CD тиесілі екендігін сөзсіз дәлелдейміз (2’’ C’’D’’ және 2’ C’D’). 1 және 2 нүктелері арқылы өтетін n түзуі, жазықтығына тиесілі, өйткені ол осы жазықтыққа тиесілі екі нүкте арқылы жүргізілген (мұндай түзулердің сансыз жиыны жүргізілуі мүмкін болатынын байқаймыз). Осы аксиома түзудің жазықтыққа тиесілігінің бірінші шарты болып табылады.
Енді n түзуі 1 түзуінің l нүктесі және m түзуінің D нүктесі арқылы өтеді, яғни n1 орнын иеленді деп болжайық. m және n түзулерінің арасындағы бұрышымен не болады? Бұл бұрыш 1 шамасына дейін азаяды. Бұдан – түзудің жазықтыққа тиесілігінің екінші шарты: егер осы жазықтықтың бір нүктесі (1)
29, а-сурет
29, б-сурет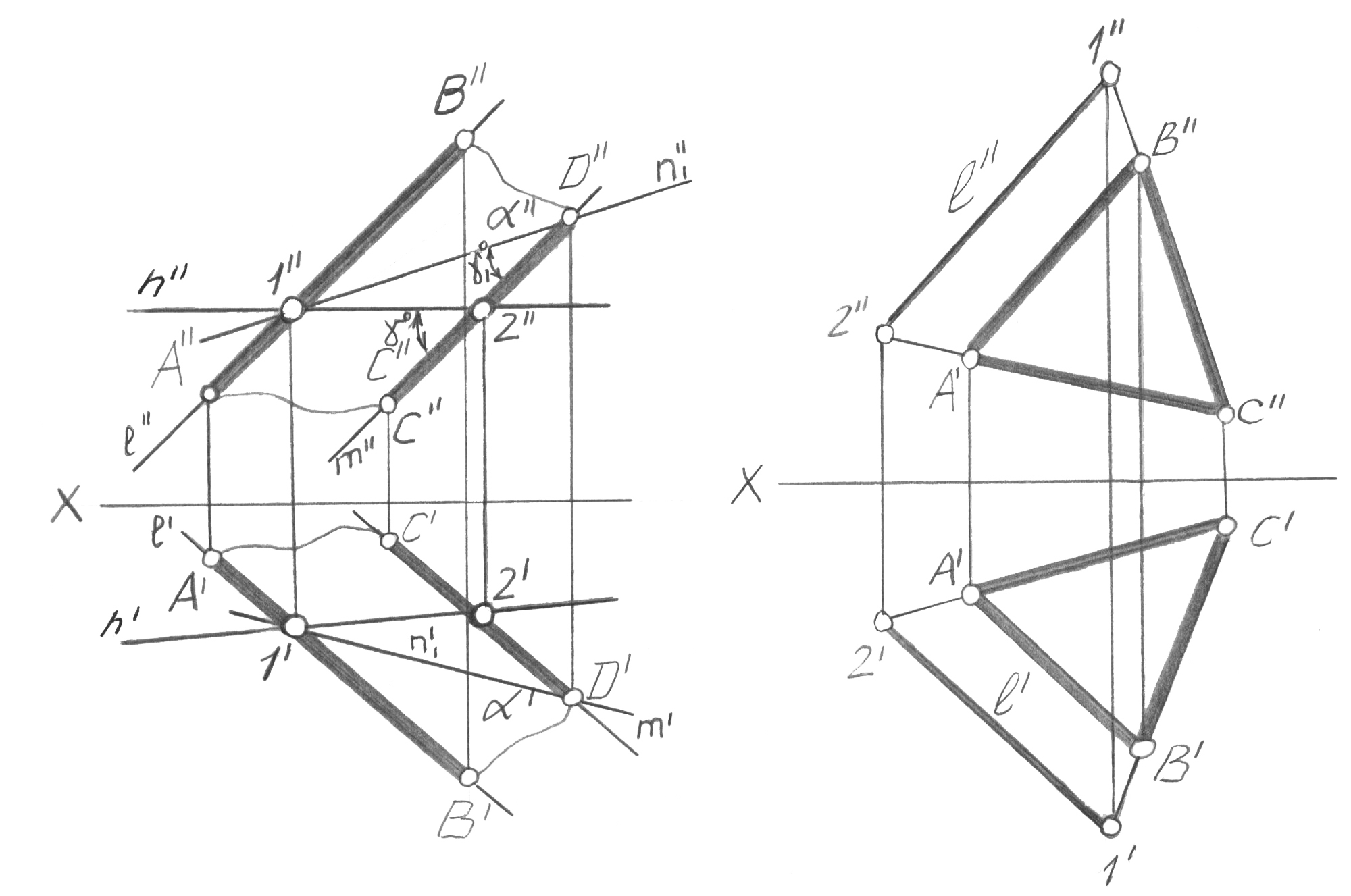
а рқылы
өтсе және осы жазықтықтың қандай да бір
түзуіне (m)
параллель болса, түзу жазықтыққа тиесілі
болады. Осы шарттың практика жүзінде
іске асыры-луы 29, б-суретте берілген.
Сіздер мұнда жазықтықтың АВС үшбұрышымен
берілгенін түсінген шығарсыздар деп
сенеміз. Сонымен бірге l
сызығы
проек-цияларының үшбұрыш проекциялары
контурынан тыс орында болуы Сізді
абыржытпасын: жазықтық кеңістікте
шексіз және сызбада қандай да бір
бейне-мен (біздің жағдайда – АВС
үшбұры-шымен) жасанды түрде шектеледі
ғой.
рқылы
өтсе және осы жазықтықтың қандай да бір
түзуіне (m)
параллель болса, түзу жазықтыққа тиесілі
болады. Осы шарттың практика жүзінде
іске асыры-луы 29, б-суретте берілген.
Сіздер мұнда жазықтықтың АВС үшбұрышымен
берілгенін түсінген шығарсыздар деп
сенеміз. Сонымен бірге l
сызығы
проек-цияларының үшбұрыш проекциялары
контурынан тыс орында болуы Сізді
абыржытпасын: жазықтық кеңістікте
шексіз және сызбада қандай да бір
бейне-мен (біздің жағдайда – АВС
үшбұры-шымен) жасанды түрде шектеледі
ғой.
Е
30-сурет ыс
кез-келген нүктені алу).
l
түзуі
жазықтығына
тиесілі, өйткені осы жазықтықтың A
және М нүктелері арқылы өтеді (A’M’,
A’’M’’
қараңыз). Осы l
түзуінде
(l’,
l’’
қараңыз) кез-келген орында D
нүктесі алынған
(D’D’’
қараңыз). Бұдан жазықтық нүктесінің
тиесілігі шарты: егер осы жазықтықтың
кез-келген түзуінде болса, нүкте
жазықтыққа тиесілі. Егер жазықтық
іздермен берілсе, онда түзу іздері
жазықтықтың онымен бір аттас іздерінде
болған (31-сурет) немесе түзу осы
жазықтықтағы іздердің біреуіне параллель
болған (32-сурет) ж
ыс
кез-келген нүктені алу).
l
түзуі
жазықтығына
тиесілі, өйткені осы жазықтықтың A
және М нүктелері арқылы өтеді (A’M’,
A’’M’’
қараңыз). Осы l
түзуінде
(l’,
l’’
қараңыз) кез-келген орында D
нүктесі алынған
(D’D’’
қараңыз). Бұдан жазықтық нүктесінің
тиесілігі шарты: егер осы жазықтықтың
кез-келген түзуінде болса, нүкте
жазықтыққа тиесілі. Егер жазықтық
іздермен берілсе, онда түзу іздері
жазықтықтың онымен бір аттас іздерінде
болған (31-сурет) немесе түзу осы
жазықтықтағы іздердің біреуіне параллель
болған (32-сурет) ж
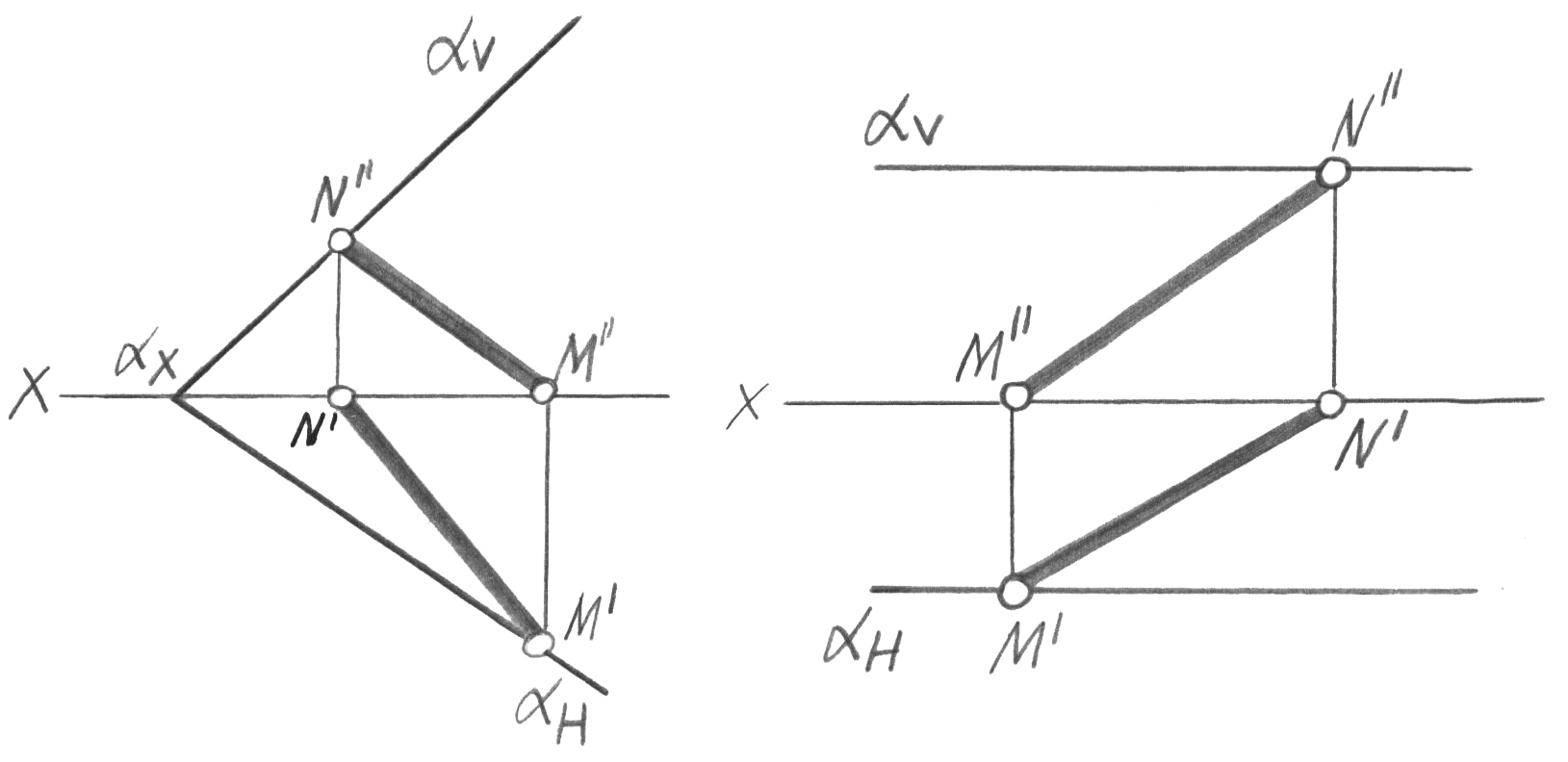 әне
басқа ізбен ортақ нүктесі бар болған
жағдайда, түзу жазықтыққа тиесілі
болады.
әне
басқа ізбен ортақ нүктесі бар болған
жағдайда, түзу жазықтыққа тиесілі
болады.
31, а-сурет
31, б-сурет
32, а-сурет
32, б-сурет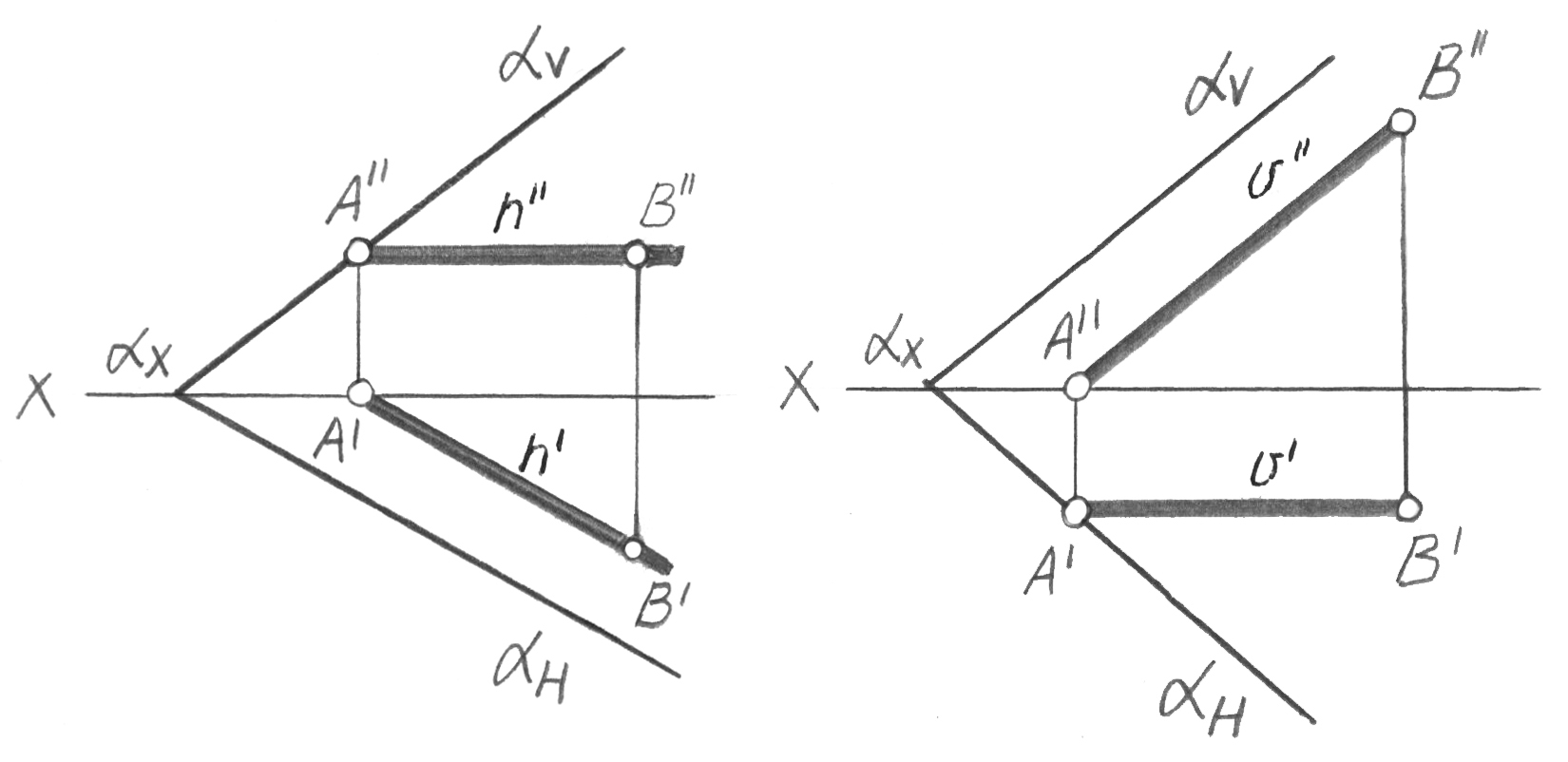
3.5 Жазықтықтың басты сызықтары
Жалпы жағдайда жазықтығының кез-келген нүктесі арқылы 6 бас (тамаша) сызық жүргізілуі мүмкін: h горизонталь, f немесе v фронталь, w про-фиаль және ең үлкен көлбеу сызығы немесе еңіс сызығы деп аталатын, олар-дың әрқайсысындағы перпендикуляр бойынша (осы жазықтықта орналасқан).
h горизонталь – жазықтығында жатқан және Н проекциясының горизонталь жазықтығына параллель түзу (33-сурет). h’’ горизонтальдың фронталь проекциясы, z аппликатасының тұрақты мәні бар сызықтары ретінде, х осіне параллель және оның үстінде орналасқан.
33, а-сурет
33, б-сурет
v
34,
а-сурет
34,
б-сурет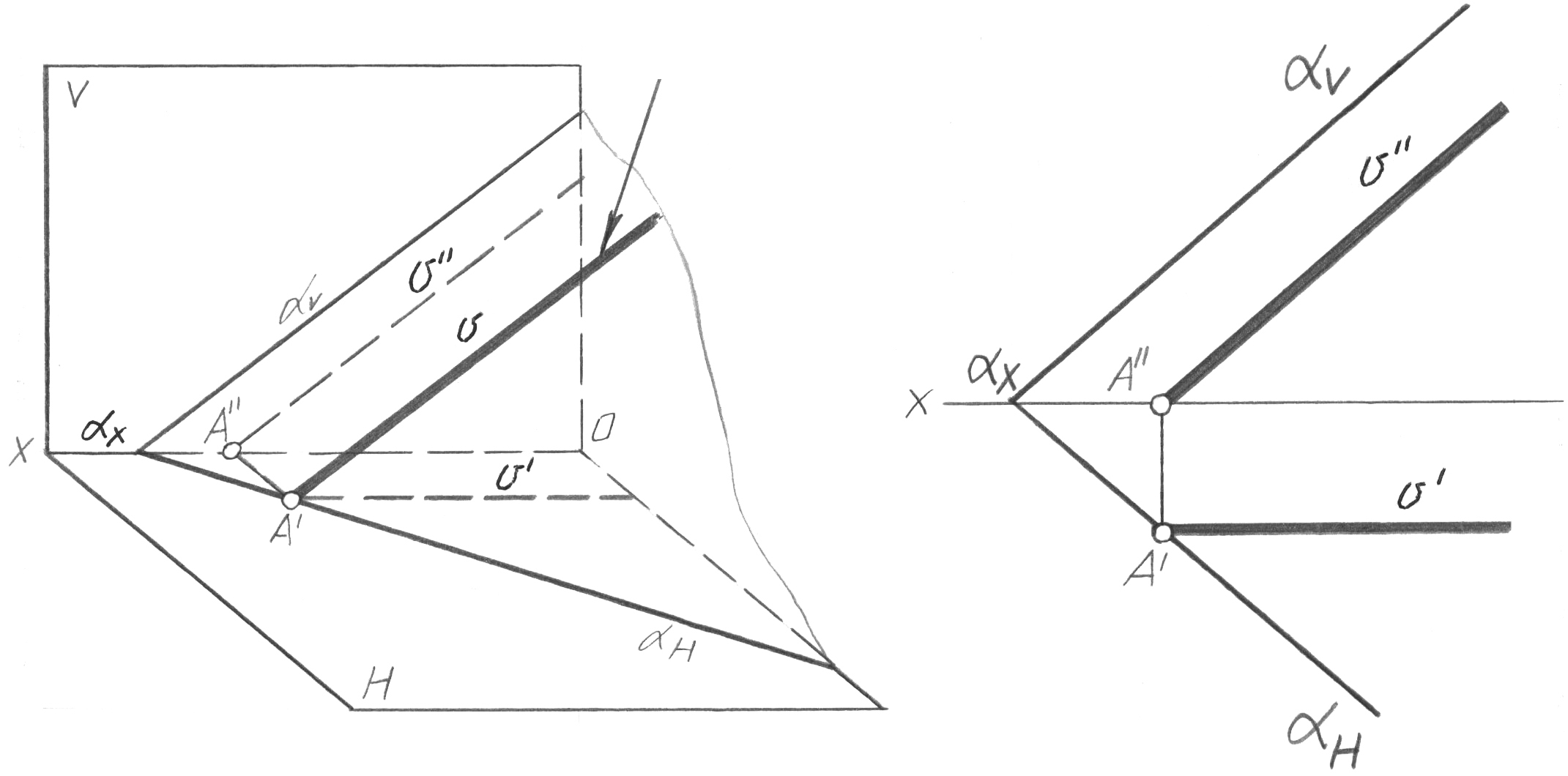
таль жазықтығына параллель түзу (34-сурет). v’ фронтальдың горизонталь проекциясы, Y ординатасының тұрақты мәні бар сызықтары ретінде, х осіне параллель және оның астында орналасқан.
w
35, а-сурет
35, б-сурет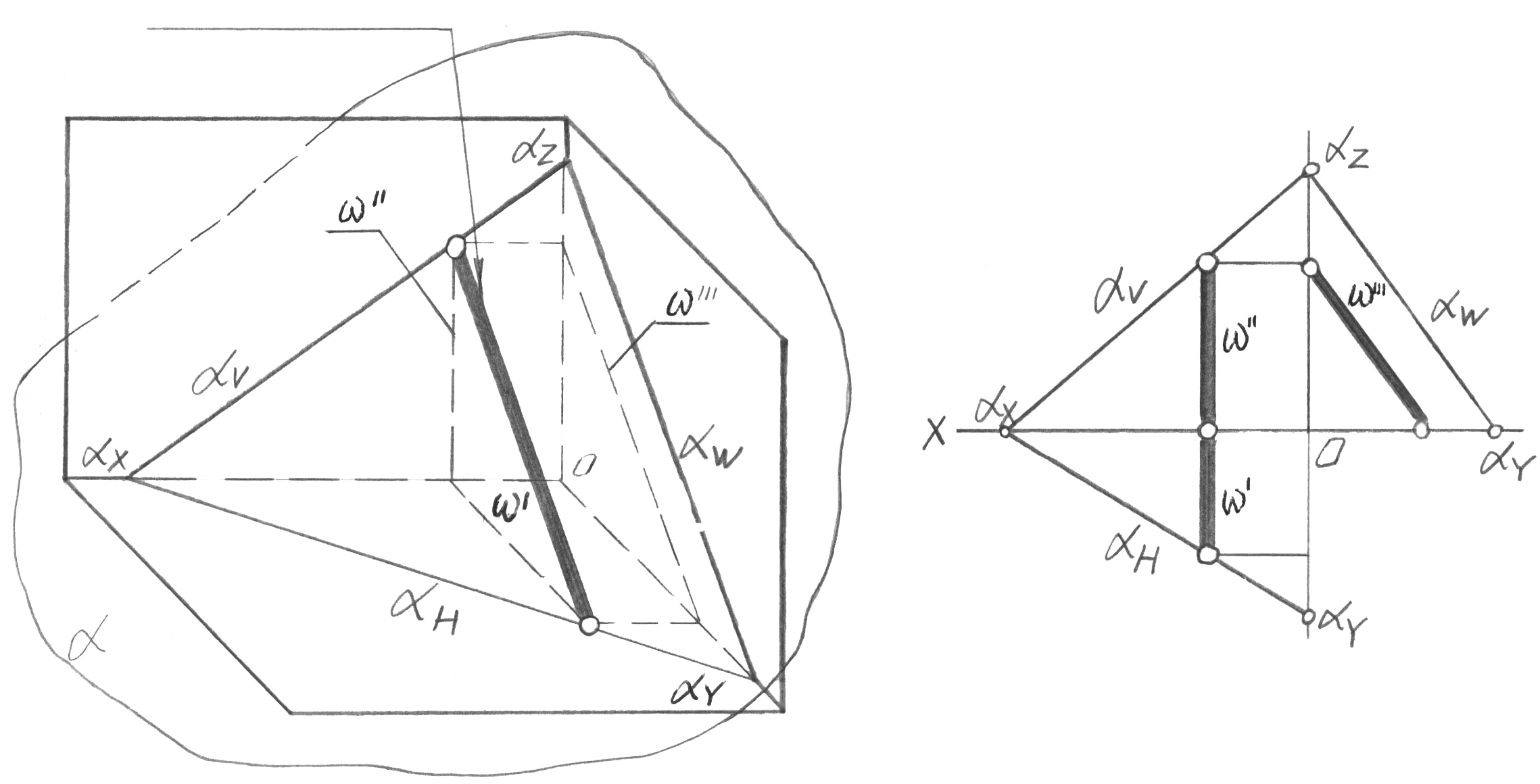
Ең үлкен еңіс сызығы – жазықтығында оның h0, h1 … hi горизонтальда-рына перпендикуляр жатқан түзу (36-сурет). Осыған ұқсас түрде жазықтығы-ның V мен W проекциялары жазықтықтарына ең үлкен еңіс сызығы салынады.
36, а-сурет
36, б-сурет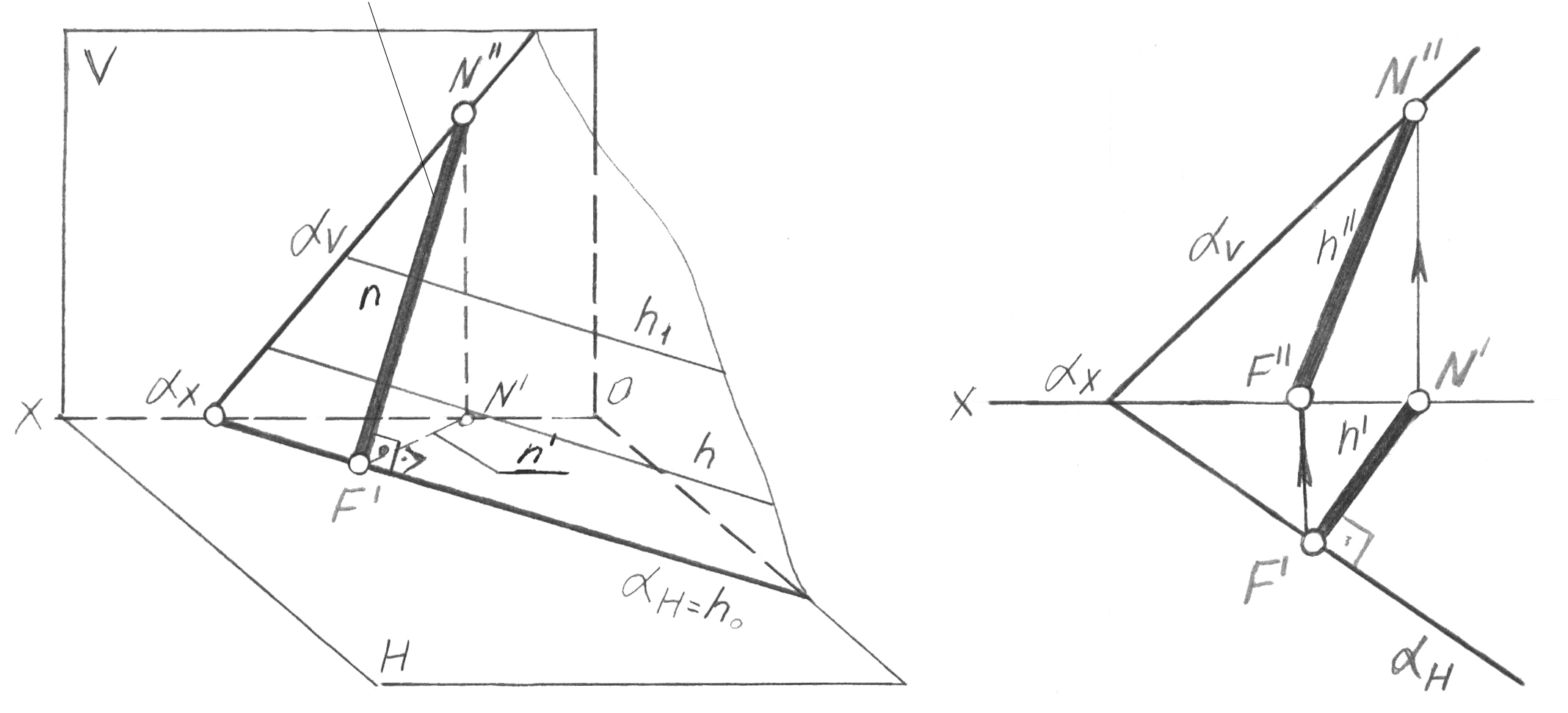
Жазықтықтың барлық бір аттас бас сызықтарының бір-біріне парал-лель екендігін, осыдан олардың бір аттас проекциялары да өз араларында параллель екендігін атап кетейік. Жазықтықтың іздері де сәйкес координатаның нөлдік мәндері бар оның басты сызықтары болып табылады: H горизонталь ізі – бұл нөлдік горизонталь (Z = 0), V фронталь ізі – нөлдік фронталь (Y = 0) және w профиль ізі – нөлдік профиаль (X = 0).
Ж
37-сурет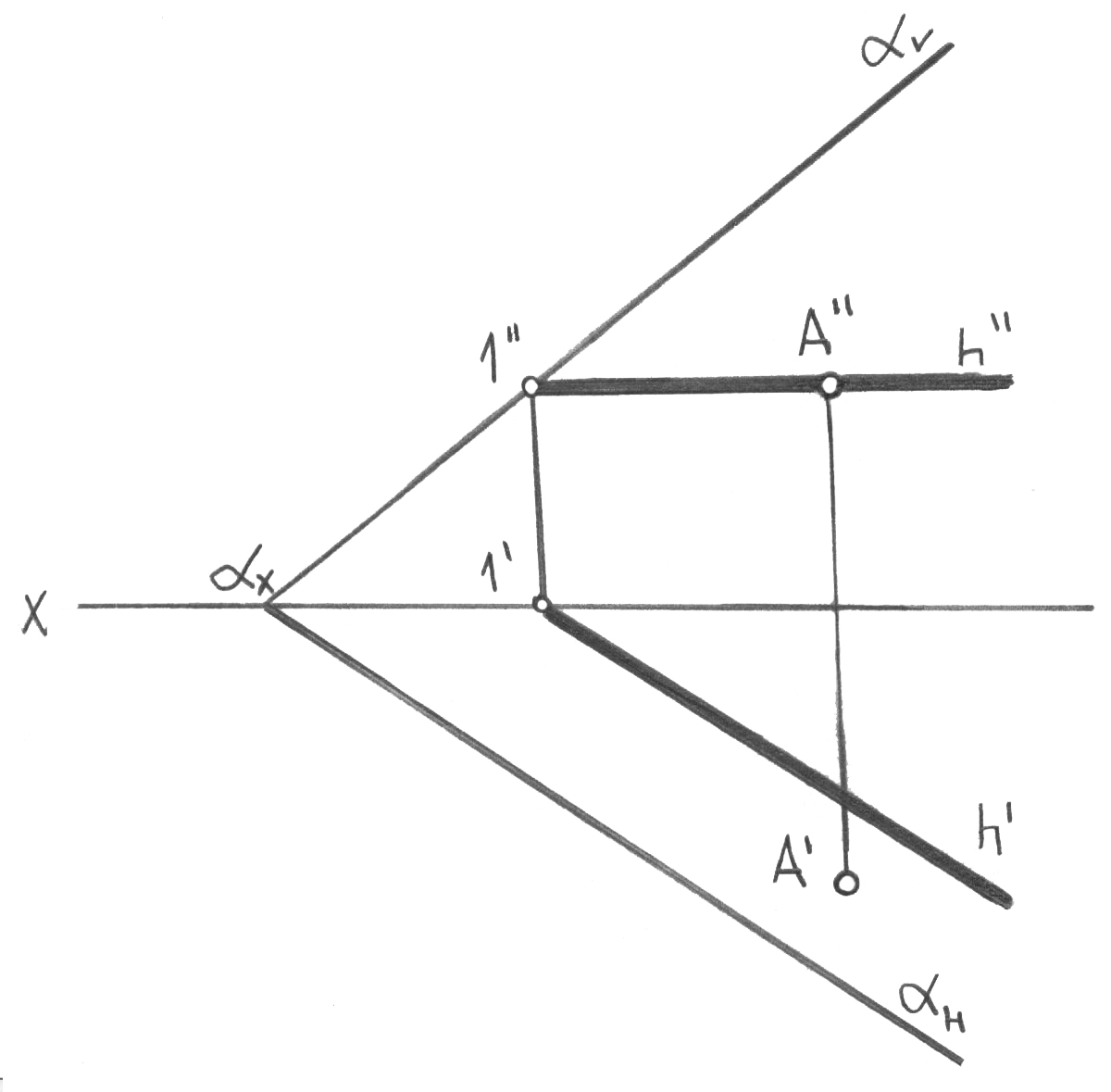
4-БӨЛІМ ПРОЕКЦИЯЛАР ЖАЗЫҚТЫҚТАРЫН ӨЗГЕРТУ ӘДІСІ
Проекцияланатын фигура проекциялар жазықтықтарына қатысты ыңғай-лы (пайдалы, ұтымды) және ыңғайсыз (пайдасыз, ұтымсыз) орында бола алады. Есептер геометриялық фигураның проекциялардың қандай да бір жазықтығы-на қатысты жеке орналасқан жағдайында едәуір оңай шешіледі. Сонымен бірге проекциялардың қандай да бір жазықтығына қатысты перпендикуляр немесе параллель орнын проекцияланатын фигураның аса пайдалы жеке жағдайы деп санау керек.
Проекциялар жазықтықтарын ауыстыру тәсілін қолданып, берілген гео-метриялық фигураны қозғалыссыз қалдырады. Проекциялардың жаңа жазық-тықтарын оларда алынатын проекциялар қарастырылатын есептің ұтымды шешімін қамтамасыз ететіндей етіп анықтайды, және де проекциялар жазық-тықтарының әрбір жаңа жүйесі ортогональ (тікбұрышты) жүйе болу керек.
38-суретте
H
және V
проекцияларының жазықтықтары жүйесінде
беріл-ген, А
нүктесі
берілген. Мұндай
жүйені
![]() деп белгілейміз. Олардың біреуін, мысалы
V,
басқа,
сондай
V1
вертикаль жазықтығымен ауыстырамыз
және осы жазықтыққа нүктенің жаңа
фронталь проекциясын саламыз. V1
жазықтығы
проекциялардың жаңа осін анықтайтын,
х1
түзуінің
бойымен Н жазықтығымен қиылысады. Н
проекцияларының горизонталь жазықтығы
екі жүйе үшін де ортақ болып табылатындықтан,
онда А
нүктесінің Z
координатасы өзгеріссіз қалады.
Проекциялар жазықтықтарының
алғашқы жүйесінен
деп белгілейміз. Олардың біреуін, мысалы
V,
басқа,
сондай
V1
вертикаль жазықтығымен ауыстырамыз
және осы жазықтыққа нүктенің жаңа
фронталь проекциясын саламыз. V1
жазықтығы
проекциялардың жаңа осін анықтайтын,
х1
түзуінің
бойымен Н жазықтығымен қиылысады. Н
проекцияларының горизонталь жазықтығы
екі жүйе үшін де ортақ болып табылатындықтан,
онда А
нүктесінің Z
координатасы өзгеріссіз қалады.
Проекциялар жазықтықтарының
алғашқы жүйесінен
![]() жаңа жүйесіне ауыстыру өзгермейтін z
координатасы
кезінде жүзеге асырылған.
жаңа жүйесіне ауыстыру өзгермейтін z
координатасы
кезінде жүзеге асырылған.
![]()
Осыдан, жаңа фронталь проекциядан жаңа х1 осіне дейінгі ара қашықтық ауыстырылатын проекциядан х осіне дейінгі ара қашықтыққа тең, яғни А1’’Ах1= = А’’Ах. Сонымен бірге А1’’ нүктесі, А нүктесінен V1 жазықтығына түсірілген перпендикулярдың негізі ретінде анықталған. А’ горизонталь проекциясына қатысты алсақ, онда ол бұрынғыдай қалады.
38, а-сурет
38, б-сурет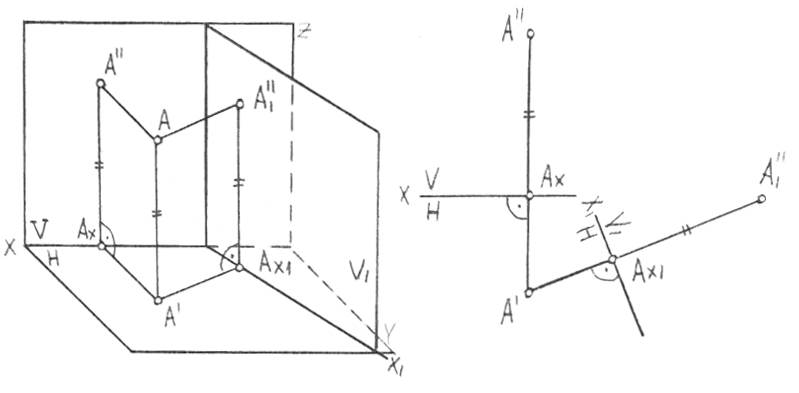
Осыған ұқсас түрде Н проекцияларының горизонталь жазықтығын V проекциясына перпендикуляр, Н1 жазықтығына ауыстыруға болады. Проекция-лардың ортогональ жазықтықтарының түрленуі келесі түрде өрнектеледі:
![]()
Бұл кезде А нүктесінің V проекцияларының екі жүйе үшін ортақ жазық-тығына дейінгі ара қашықтығын анықтайтын, Y координатасының шамасы өзгермейді (39-сурет).
39, а-сурет
39, б-сурет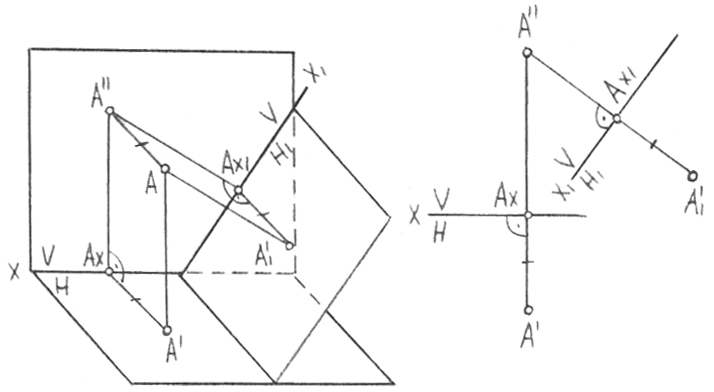
Сондықтан А1’Ах1 = А’Ах. Эпюрде нүктенің жаңа проекциясын салған кезде (39, б-сурет), А’’-дан x1 жаңа осіне перпендикуляр түсірілген, онда Ах1 нүктесінен А нүктесінің Y координатасына тең, А1’Ax1 кесіндісі қалдырылған. Проекциялар жазықтықтарының бір жүйесінен екіншіге жүйелі өтуді, келесі ережені орындай отырып, жүзеге асыру керек. Нүктенің жаңа проекциясынан жаңа оське дейінгі ара қашықтық нүктенің түрленетін (ауыстырылатын) проекциясынан алдыңғы оське дейін ара қашықтыққа теңестірілу керек. Егер қарастыру объектісі нүкте емес, кез-келген басқа геометриялық объект болып табылса, мұндай түрлендірулер әрбір оған тән нүкте үшін жүргізіледі. Сонымен бірге әрбір кезеңде жаңа осьтің орны ерікті түрде емес, ал нақты графикалық есепті шешу үшін қалай пайдалы болатын түрде беріледі.
Проекциялар жазықтықтарын ауыстыру тәсілімен шешілетін барлық есептерді келесі төрт есептің біреуіне келтіруге болады.
1-есеп. Жалпы орналасқан түзу жаңа жүйенің проекциялары жазықтықта-рының біреуіне параллель болатындай етіп, сызбаны түрлендіру керек.
4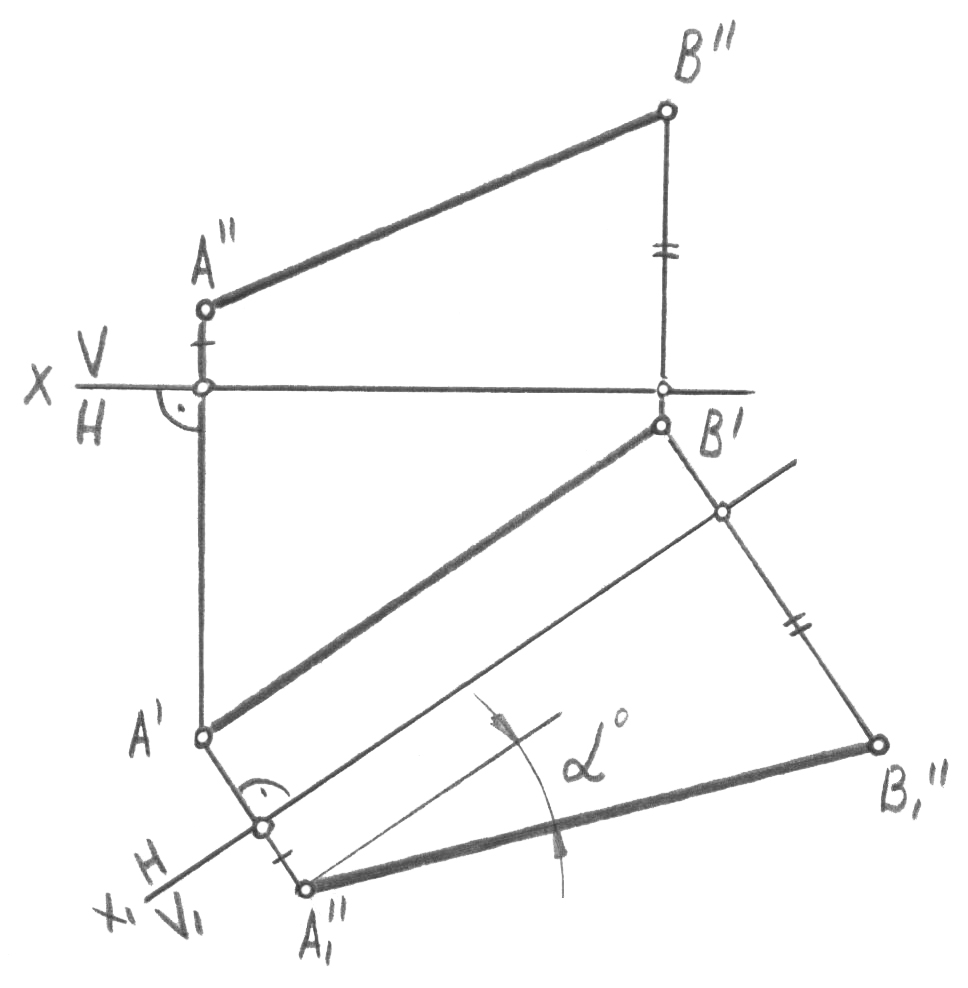 0-суретте
[АВ] түзуінің кесіндісі көрсетілген, ол
проекциялар жазық-тықтарының алғашқы
жүйесінде жалпы орында алады.
0-суретте
[АВ] түзуінің кесіндісі көрсетілген, ол
проекциялар жазық-тықтарының алғашқы
жүйесінде жалпы орында алады.
Е
40-сурет
дықтан натурал шамаға проекцияланды. [A1’’B1’’] проекциясы және x1 осі арасындағы бұрыш [AB] кесіндісінің Н жазықтығына 0 көлбеу бұрышы болып табылады [A1’’B1’’] = [AB].
Осы есепті Н проекцияларының горизонталь жазықтығын Н1-ге ауысты-румен де шешуге болады (41-сурет). Н1 жаңа жазықтығы V перпендикуляр және [AB] кесіндісіне параллель орналасқан, ал жаңа ось х1 || [AB]. [A1’B1’] = [AB] және [A1’B1’] проекциясымен және х1 осімен құрылған, 0 бұрышының, [AB] түзуі кесіндісінің V жазықтығына көлбеу бұрышына тең екендігі анық.
41-сурет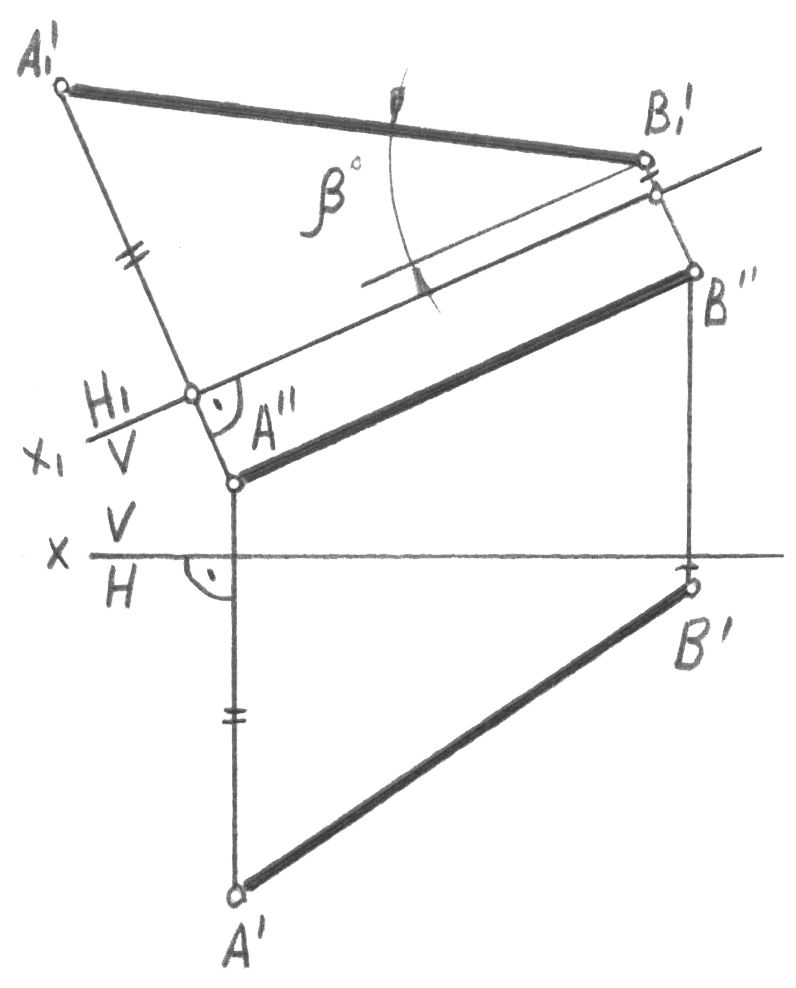
2-есеп. Жалпы орналасқан түзу жаңа жүйенің проекциялары жазықтықта-рының біреуіне перпендикуляр болатындай етіп, сызбаны түрлендіру керек.
Жалпы орналасқан түзу проекцияларының біреуін нүктеге түрлендіру жазықтықтарды екі рет ауыстыруды талап етеді, өйткені жүйесінде түзуге перпендикуляр жазықтық, не Н-қа да, не V-ға да ортогональ болмайды.
жүйесінен жүйесіне өткен кезде V1 жазықтығын Н-қа перпен-дикуляр және [AB] түзуіне параллель етіп орналастырады (42-сурет), яғни жоғарыда қарастырылған, бірінші есепті шешеді.
Екінші
рет
ауыстырған
кезде
жаңа
Н1
жазықтығын
[AB] түзуінің
кесіндісіне
перпендикуляр,
яғни
х2
A1’’B1’’
орналастырады.
Мұнымен
V1
және Н1
ортогональдылық шарты қамтамасыз
етілетін болады. Бұл кезде Y
= const
мәні алғашқы
жүйесінен емес, ал біз оны түрлендіретін,
яғни одан соңғы
![]() жүйесіне ауысатын,
жүйесінен алынады. Н1
жазықтығында түзу нүктемен бейнеленеді.
Соны-мен,
жүйесінде түзу Н1
жазықтығына
қатысты проекция-лаушы болды. Берілген
есепті ал-
жүйесіне ауысатын,
жүйесінен алынады. Н1
жазықтығында түзу нүктемен бейнеленеді.
Соны-мен,
жүйесінде түзу Н1
жазықтығына
қатысты проекция-лаушы болды. Берілген
есепті ал-
дымен
Н
42-сурет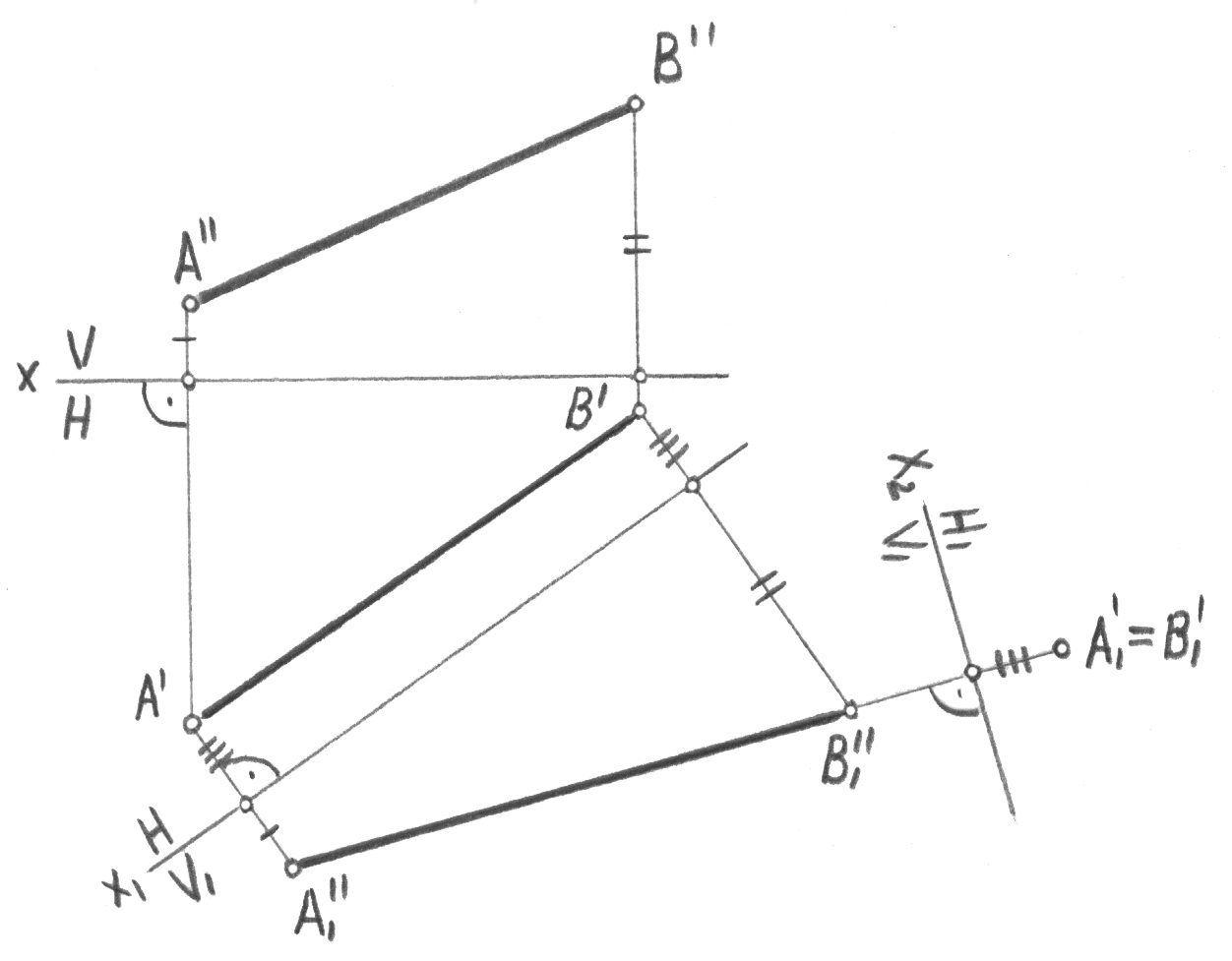
![]() -
42-сурет үшін
-
42-сурет үшін
![]() -
43-сурет үшін
-
43-сурет үшін
43-сурет
3-есеп. Проекциялар жазықтықтарының жаңа жүйесінде жалпы орналас-қан жазықтық проекциялаушы болатындай, сызбаны түрлендіру керек.
44-сурет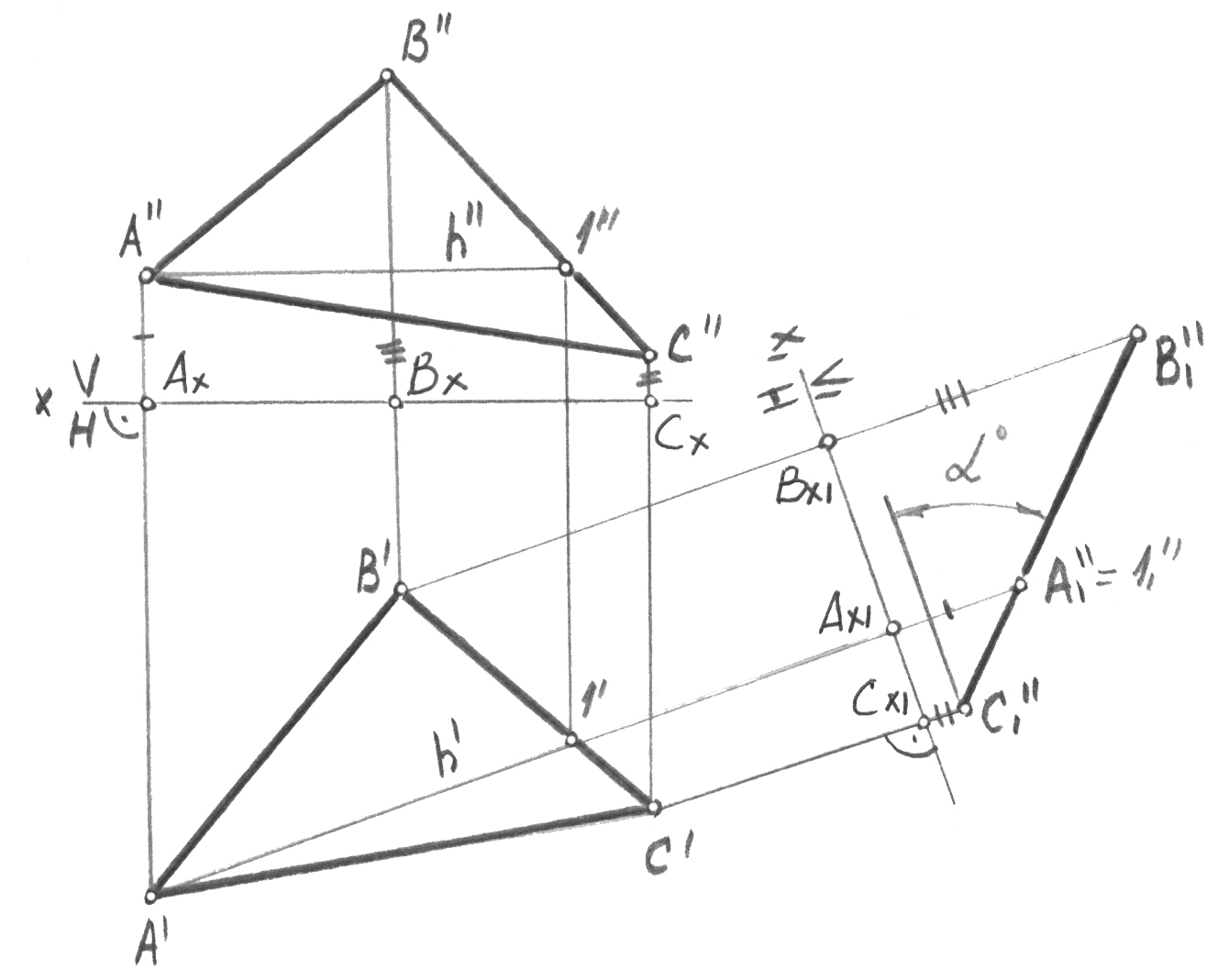
Жалпы орналасқан жазықтық А, В, С үш нүктесімен берілген болсын (44-сурет). Қойылған есепті шешу үшін проекциялардың жаңа жазықтығын АВС және проекциялар жазықтықтарының біреуіне перпендикуляр етіп орналастыру қажет. Ендеше, проекциялардың жаңа жазықтығы берілген жазық-тықта орналасқан, қандай да бір түзуге перпендикуляр болу керек. Мұндай түзу ретінде бағыты әдейі белгілі болатын, АВС үшбұрышы жазықтығының кез-келген h горизонтальды алған ыңғайлы. V1 h (яғни х1 h’) орналас-тырумен бірден екі шарттың орындалуы қамтамасыз етіледі: проекциялардың жаңа жазықтығы V1 H және V1 АВС, сондықтан жаңа х1 осін h1 (яғни A’1’) етіп жүргіземіз. АВС үшбұрышы төбелерінің А’B’C’ горизонталь проекциялары арқылы жаңа оське перпендикуляр түзулер жүргізіп, осы түзулерде х1 осінен Ax1A1’’ = AxA’’, Bx1B1’’ = BxB’’, Cx1C1’’ = CxC’’ кесінділерін қалдырамыз. Осылай түзу сызықты білдіретін, АВС үшбұрышының жаңа А1’’B1’’C1’’ фронталь проекциясы алынады. Үшбұрышқа және Н-қа перпен-дикуляр V1 жазықтығына, үшбұрышпен және Н проекциясының жазықтығымен құрылған, 0 бұрышы бұрмаланусыз проекцияланады.
Осыған ұқсас түрлендіру 45-суретте орындалған, онда Н жазықтығы V-ға және АВС үшбұрышына перпендикуляр Н1 жазықтығымен ауыстырылған. Ол үшін үшбұрыш жазықтығында, оған Н1 жазықтығы перпендикуляр орнала-сатын, V = A1 фронталь жүргізілу керек. Сондықтан жаңа x1 осі v’’=A’’1’’ перпендикуляр таңдалған. Үшбұрыш жазықтығы Н1 қатысты проекциялаушы болды. Н1 жазықтығына үшбұрыштың V проекцияларының фронталь жазықты-ғына 0 көлбеу бұрышы бұрмаланусыз проекцияланады.
45-сурет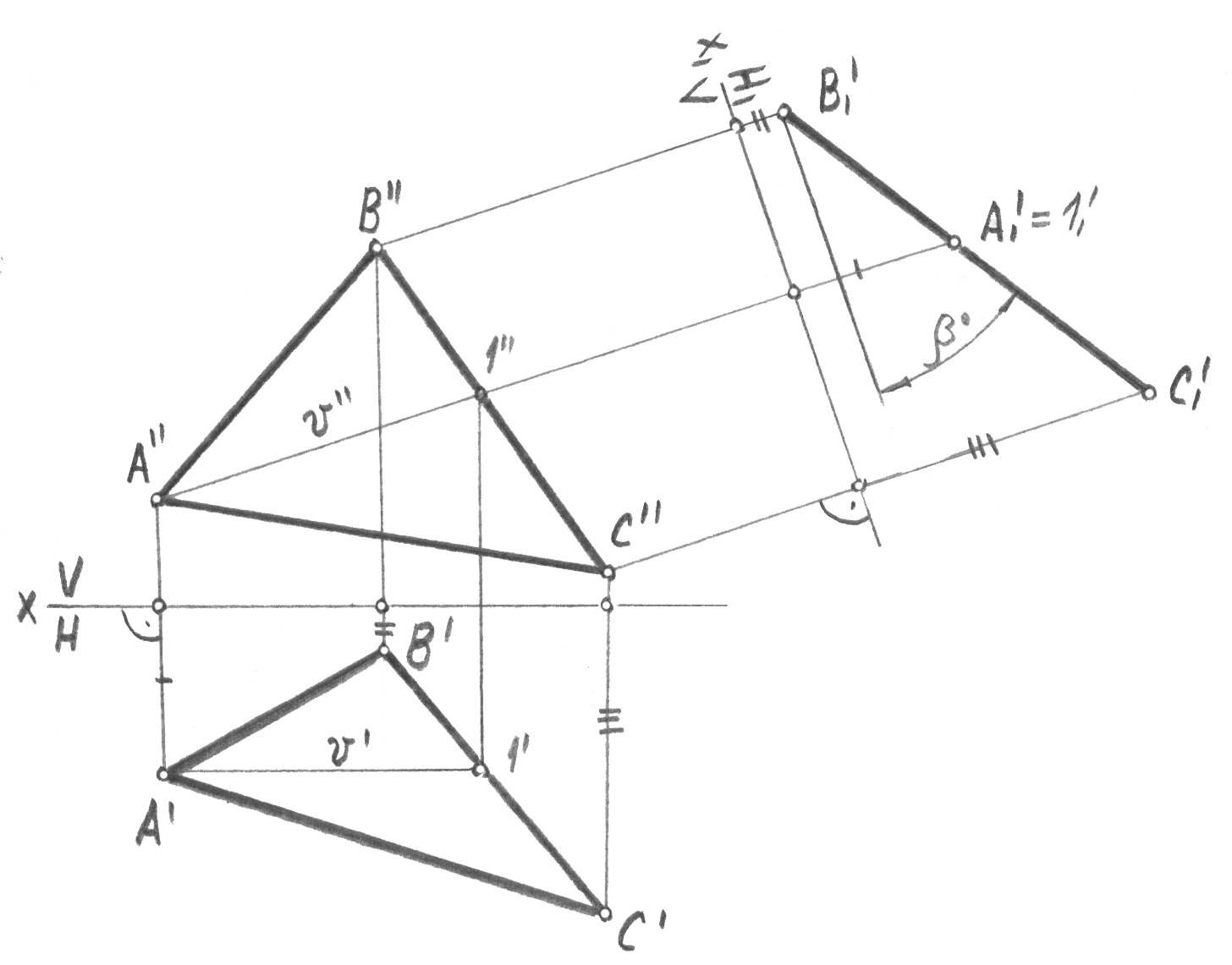
4-есеп. Жалпы орналасқан жазықтық жаңа жүйе проекциялар жазықтық-тарының біреуіне параллель болатындай, сызбаны түрлендіру керек.
жүйесінде жалпы орналасқан АВС үшбұрышы берілген болсын. Проекциялар жазықтықтарының осындай жаңа ортогональ жүйесін құру керек, онда олардың біреуі үшбұрышқа параллель болу керек. жүйесінде мұндай жазықтықты салуға болмайды, өйткені үшбұрышқа параллель жазықтық не Н-қа, не V-ға перпендикуляр болмайтындықтан, яғни ол проекциялар жазықтық-тарымен ортогональ жүйе құрамайды.
Есепті
шешу проекциялар жазықтықтарын екі
рет айырбастауды талап етеді (46-сурет).
Бірінші айырбастау
![]() үшбұрышты проекция-лаушы жазықтыққа
түрлендіруден тұрады. Бұл процесс
жоғарыда сипатталған (44, 45-есептердің
шешімін қараңыз).
үшбұрышты проекция-лаушы жазықтыққа
түрлендіруден тұрады. Бұл процесс
жоғарыда сипатталған (44, 45-есептердің
шешімін қараңыз).
46-сурет
Есепті
шешудің екінші кезеңі
![]() жүйесінен
жүйесінде Y
– const
болғанда
жүйесіне өтуден тұрады (46-сурет).
жүйесінен
жүйесінде Y
– const
болғанда
жүйесіне өтуден тұрады (46-сурет).
Н1 жаңа жазықтығы х2 осіне параллель анықталады, оған салынған пер-пендикулярларда В1’Bx2 = B’Bx1, A1’Ax2 = A’Ax1, С1’Сx2 = С’Сx1 ара қашықтық-тарын қалдырамыз ( жүйесіндегі әрбір нүктенің Y = const координатасы-ның мәні). Салынған A1’B1’C1’ проекциясы АВС ақиқат шамасын анықтайды.
Осыған ұқсас берілген есепті проекциялар жазықтықтары жүйесін екі рет ауыстырумен шешуге болады.
(47-сурет)
Проекциялар жазықтықтарын өзгерту әдісін пайдалану арқылы сондай-ақ геометриялық фигуралардың өзара тиесілігін анықтауға және беттерді берілген пішіннің алдында салуға арналған есептер шешіледі.

47-сурет
5-БӨЛІМ БЕТТЕРДІ ПРОЕКЦИЯЛАУ
5.1 Негізгі ұғымдар және анықтамалар
Бет дегеніміз – оның қозғалысы мен пішіні белгілі заңға бағынған, l сызығының l1, l2 … li тізбекті орындарының жиыны. Заң деп l сызығының кеңістікте әрбір жаңа орында l1, l2 … li жиынының мүшелері бет қабықшасын құрай отырып, бір-біріне жанасатындай орын ауыстыру сипатын, тәртібін, ережелерін, траекториясын түсіну керек.
Б
Образующая –
құраушы;
Направляющая
- бағыттаушы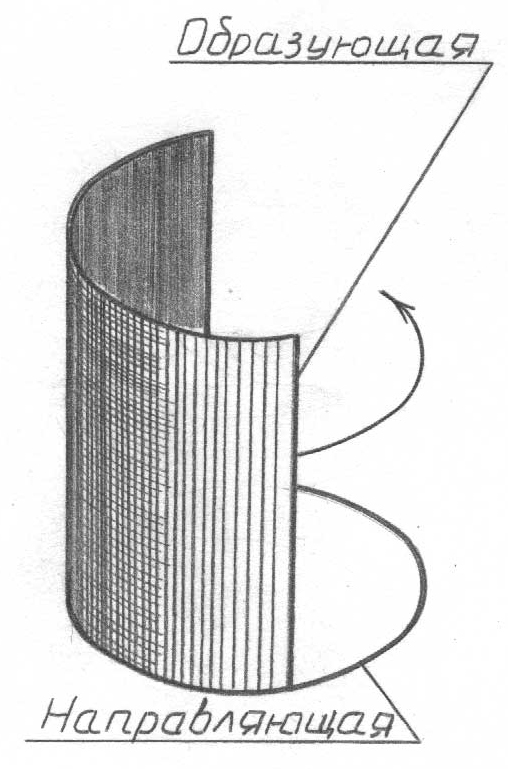
48, а-сурет
48, б-сурет
т үрін
сақтай отырып, біз бірінші жағдай үшін
- призмалық, ал екінші үшін пирамидалық
беттерді алушы едік. Және бұл, тағы да,
құраушының орын ауыстыру заңының
өзгеруі есебінен (шеңбер бойынша емес,
ал көпбұрыш бойынша) болады.
үрін
сақтай отырып, біз бірінші жағдай үшін
- призмалық, ал екінші үшін пирамидалық
беттерді алушы едік. Және бұл, тағы да,
құраушының орын ауыстыру заңының
өзгеруі есебінен (шеңбер бойынша емес,
ал көпбұрыш бойынша) болады.
Б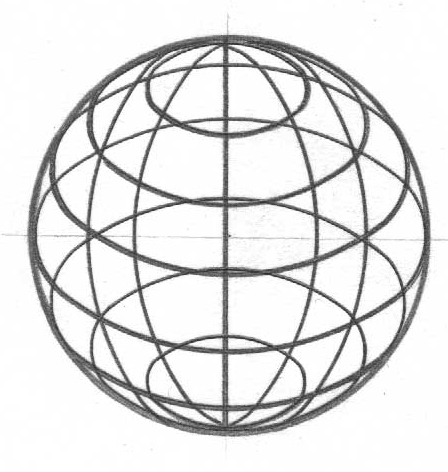
 еттің
дискретті қаңқасы – бұл бетті кеңістікте
және сызбада беретін, құраушылардың
және бағыттаушылардың (немесе нүктелердің)
соңғы жиыны. Терминді беттің тіректі
сызықтарының торы ретінде дәлме-дәл
түсіну керек. 49-суретте жалпы түрдегі
сфералық беттің (49, а-сурет) және конустық
беттің (49, б-сурет) дискретті қаңқалары
берілген. Күрделі бетке қатысты сызбаны
салу оның дискретті қаңқасының проекциясын
салуға келтіріледі. 50, а-суретте жалпы
түрдегі конустық беттің сызбасы
берілген, оның дискретті қаңқасы 49,
б-суретте көрсетілген. Олардың құрылу
заңы айқын көрсетілген, қарапайым беттер
үшін (сфера, дөңгелек конус, дөңгелек
цилиндр және т.б.) дискретті қағқаны
салудың қажеттілігі жоқ, өйткені олардың
әрқайсысы олардың сыртқы контурының
проекцияларымен (очерктермен, 50, б-сурет)
толық берілуі мүмкін.
еттің
дискретті қаңқасы – бұл бетті кеңістікте
және сызбада беретін, құраушылардың
және бағыттаушылардың (немесе нүктелердің)
соңғы жиыны. Терминді беттің тіректі
сызықтарының торы ретінде дәлме-дәл
түсіну керек. 49-суретте жалпы түрдегі
сфералық беттің (49, а-сурет) және конустық
беттің (49, б-сурет) дискретті қаңқалары
берілген. Күрделі бетке қатысты сызбаны
салу оның дискретті қаңқасының проекциясын
салуға келтіріледі. 50, а-суретте жалпы
түрдегі конустық беттің сызбасы
берілген, оның дискретті қаңқасы 49,
б-суретте көрсетілген. Олардың құрылу
заңы айқын көрсетілген, қарапайым беттер
үшін (сфера, дөңгелек конус, дөңгелек
цилиндр және т.б.) дискретті қағқаны
салудың қажеттілігі жоқ, өйткені олардың
әрқайсысы олардың сыртқы контурының
проекцияларымен (очерктермен, 50, б-сурет)
толық берілуі мүмкін.
49, а-сурет
49, б-сурет
50, а-сурет
50, б-сурет
Б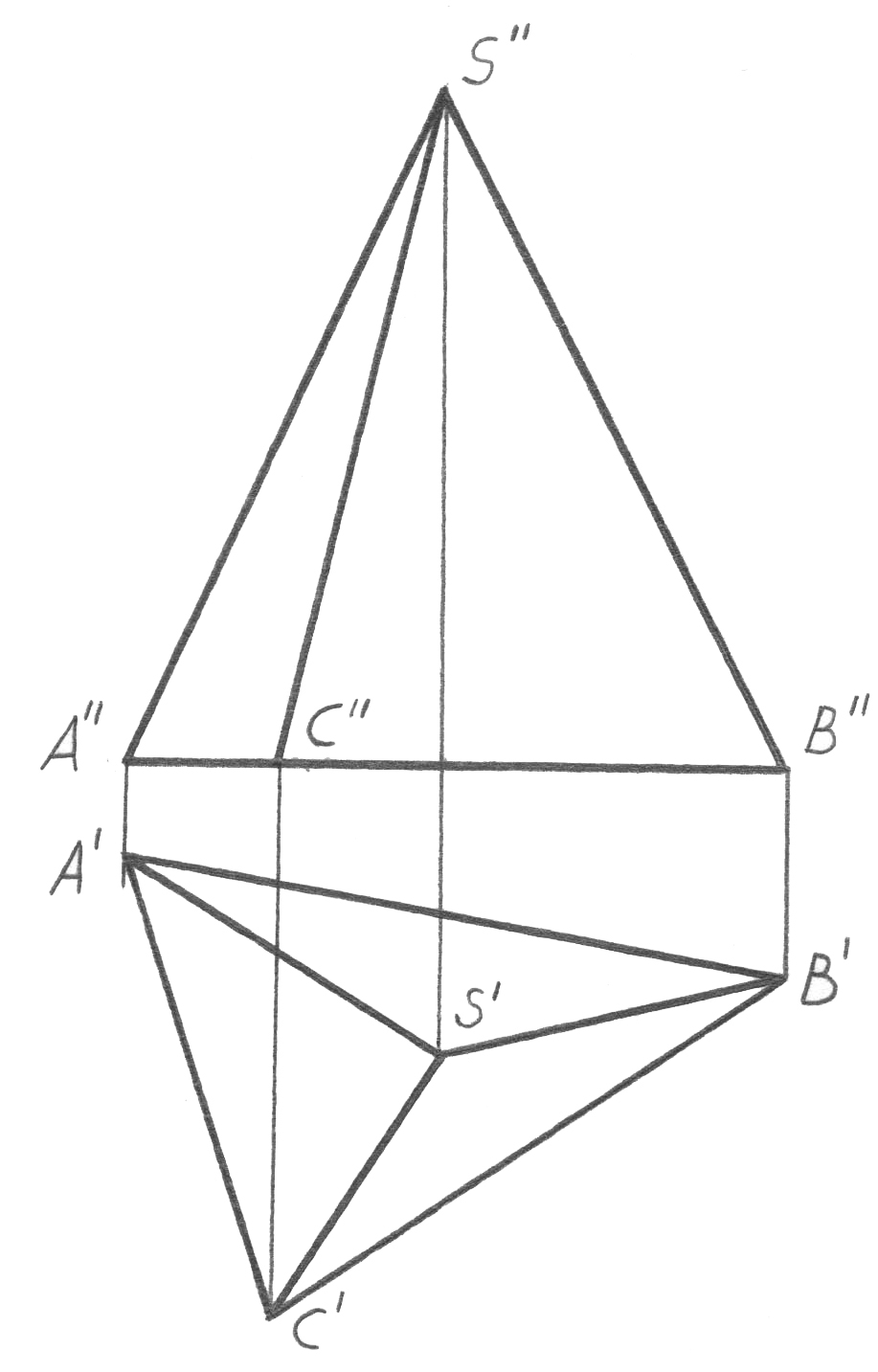
 еттің
«очеркі» және беттің «проекциясы»
терминдерін ажырату керек. «очерк»
терминіне қатысты проекцияның сыртық
сызықтарын шектейтін, тек сыртқы контур
проекциялары туралы ғана сөз болып
отыр. Салыстыру үшін 51, а-суретте –
пирамиданың сызбасы, ал 51, б-суретте осы
беттің очерктері берілген. Жоғарыда
айтылған ойықтары, қиылысулары және
т.б. жоқ, дөңгелек конус, дөңгелек цилиндр
және сфера үшін, очерктер мен проекциялар
сәйкес келеді (50, б-сурет).
еттің
«очеркі» және беттің «проекциясы»
терминдерін ажырату керек. «очерк»
терминіне қатысты проекцияның сыртық
сызықтарын шектейтін, тек сыртқы контур
проекциялары туралы ғана сөз болып
отыр. Салыстыру үшін 51, а-суретте –
пирамиданың сызбасы, ал 51, б-суретте осы
беттің очерктері берілген. Жоғарыда
айтылған ойықтары, қиылысулары және
т.б. жоқ, дөңгелек конус, дөңгелек цилиндр
және сфера үшін, очерктер мен проекциялар
сәйкес келеді (50, б-сурет).
51, а-сурет
51, б-сурет
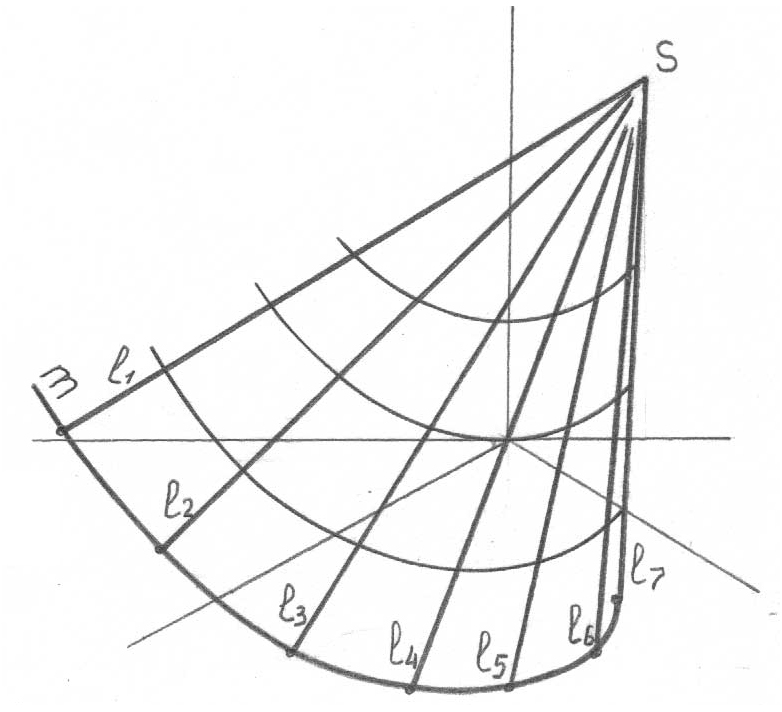
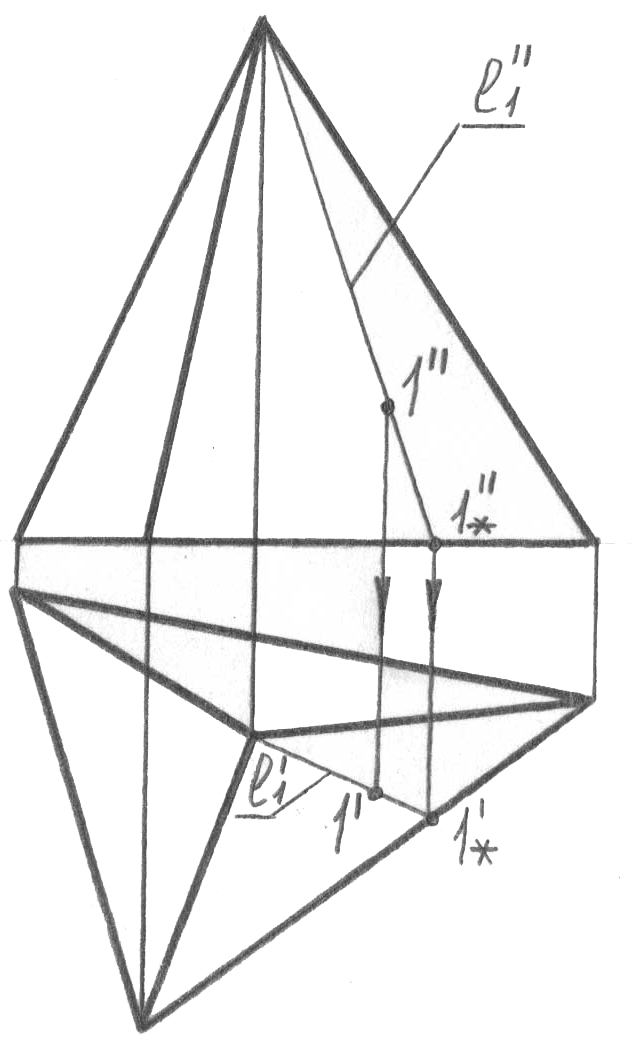
Беттің үздіксіз қаңқасы – бұл бетті оның әрбір нүктесі арқылы осы жиынның жалғыз сызығы ғана жүргізілуі мүмкін болатындай толтыратын, l сызығының l1, l2 … li тізбекті орындарының жиыны. Біздің курс шеңберінде термин көбінесе теориялық сипатта болады, бірақ аса маңызды практикалық тезисті білдіреді: БЕТТІҢ КЕЗ-КЕЛГЕН НҮКТЕСІ АРҚЫЛЫ ЖАЛҒЫЗ ҒАНА ҚҰРАУШЫ ЖҮРГІЗІЛУІ МҮМКІН. Осы тезис олардың әрқайсысындағы олардың жалғыз ғана орнын алдын ала анықтап, беттегі нүктелердің жетіс-пейтін проекцияларын салу негізінде жатыр.
Б
52, а-сурет
52, б-сурет
Сызбада бетті толық беру критерийі осы нүктенің берілген проекция-сының біреуі бойынша беттегі нүктенің жетіспейтін проекцияларын салу мүмкіндігі болып табылады. Беттегі нүктенің жетіспейтін проекциясын салу үшін жалпы жағдайда қажет:
нүктенің берілген проекциясы арқылы (1”, 53, а-сурет) құраушы проекциясын жүргізу (l”, 53, б-сурет);
бетті құрастыру заңы бойынша осы құраушының жетіспейтін проекциясын салу (l’, 53, в-сурет);
проекциялық байланыс сызығы бойынша одан осы нүктенің жетіс-пейтін ізделіп отырған проекциясын табу (1’, 53, г-сурет).
Б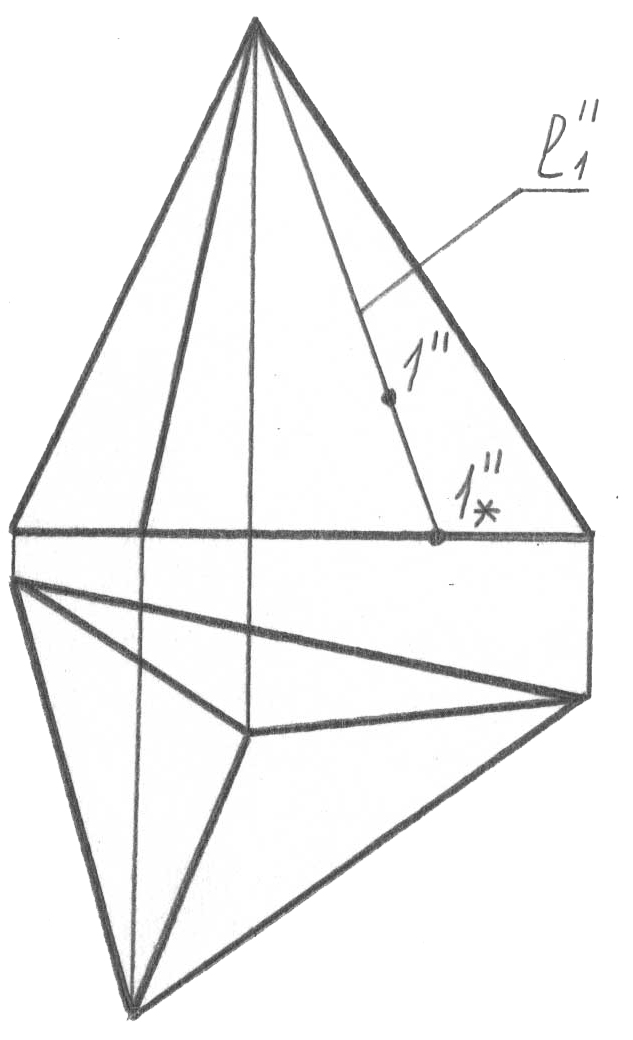 еттің
үздіксіз қаңқасын қалыптастыру негізінде
беттің кез-келген нүктесі арқылы жалғыз
құраушы жүргізілуі мүмкін болғандықтан,
алынған шешім де (1’ нүктесінің) жалғыз
болады.
еттің
үздіксіз қаңқасын қалыптастыру негізінде
беттің кез-келген нүктесі арқылы жалғыз
құраушы жүргізілуі мүмкін болғандықтан,
алынған шешім де (1’ нүктесінің) жалғыз
болады.
53, а-сурет
53, б-сурет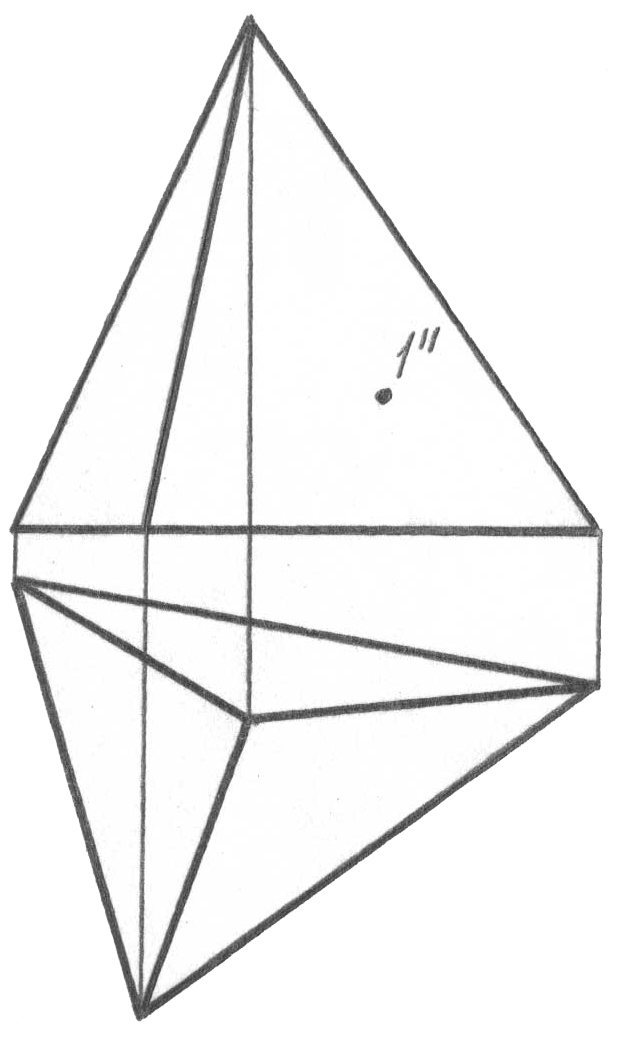
5.2 Беттердің жіктелуі
Мұнда ұсынылып отырған беттердің жіктелуі барлық мүмкін болатын жіктеу белгілері шеңберінде минимум бөлігін алатын, ең қарапайым болып табылатынын алдын ала байқаймыз. Сондай-ақ біздің сызба геометрия циклін-де «Беттер» бөлімінің беттің қоршаған ортамен өзара әрекеттесуін есепке алмай, өткелдері бар бөлшектердің пішін үйлесімін құрастыру көзқарасынан ғана қарастырылатынын да назарға алу керек.
Беттердің жіктелуін екі жіктеу белгілері бойынша қарастырамыз.
53, в-сурет
53, г-сурет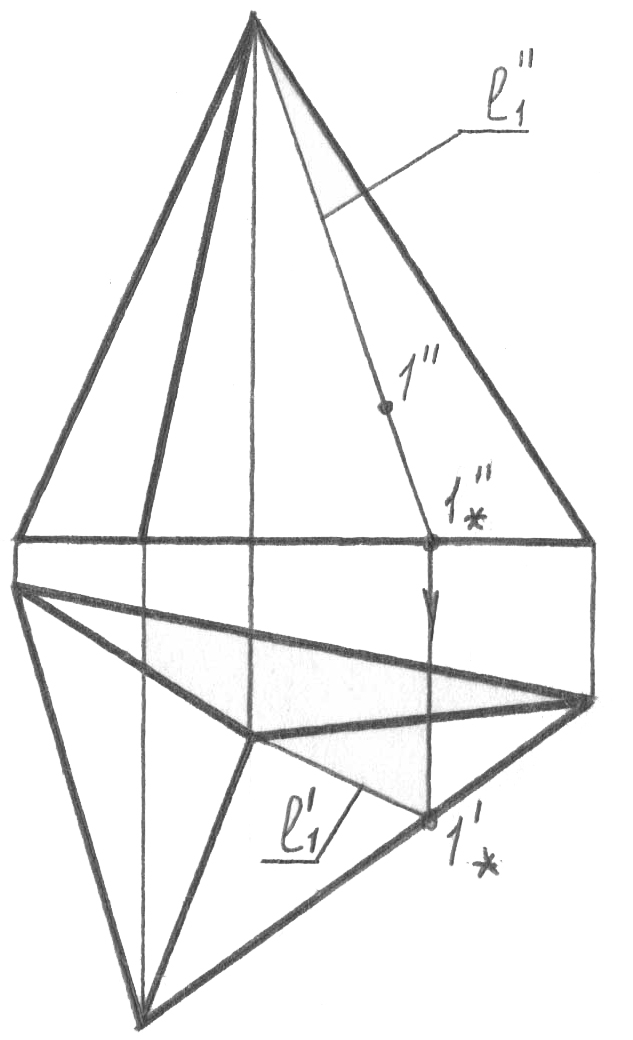
Құраушы
пішініне байланысты б
54-сурет
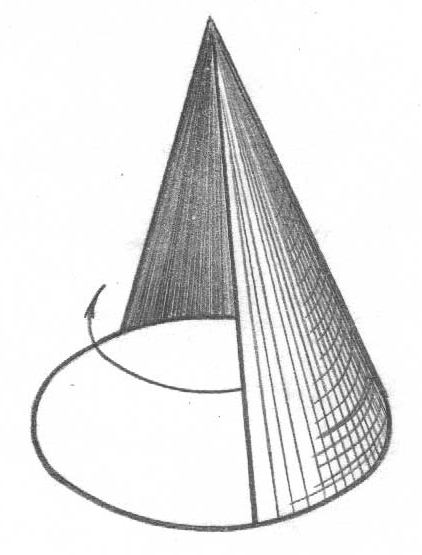
Құрастыру заңына (құраушының орын ауыстыру сипатына) байланысты беттер былай бөлінеді:
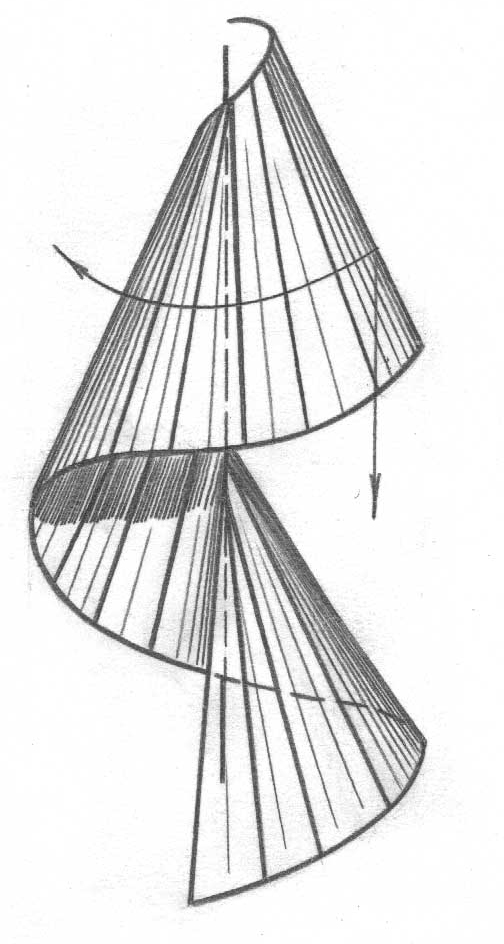
бұрандалы (бұрандалар, шнектер, бұрамдықтар, бұрғылар және т.б. – құраушының осьтің маңайында және оның бойымен айналмалы-үдемелі орын ауыстыру арқылы құрастырылады (55-сурет);
айналымды, - тік сызықты немесе қисық сызықты құраушы-ның (доғалар, шеңбер, жалпы түр-дегі қисық) ось маңында айналуы-мен құрылады. Солай цилиндрлік, конустық, сфералық, торлық және т.б. беттер құрылады (48, 49, 52-беттер);
55-сурет
параллелизм жазықтығы бар беттер (Каталана); әрбір l1, l2 … li орнала-суында құраушы берілген жазықтығына алдынан параллель болып қалатындай (парал-лелизм), m және n тік сызықты немесе қисық сызықты екі бағыт бойынша (56-сурет) l тік сызықты құраушының орын ауыстыруымен құрастырылады.
Жоғары және аса жоғары жылдамдықтар кезінде орта (газ, сұйықтық және т.б.) қатты дене ретінде (турбина жасау, авиация, космонавтика, әскери салалар) қарастырылатын, олармен жұмыс істейтін өнеркәсіп салалары үшін, инженерлік графиканың «Беттер» бөлімі негіз құраушы болып табылады, өйткені беттер геометриясы арқылы бұйымдардың пайдаланушылық, эконо-микалық және өзге (аса жоғары ретті) қасиеттері анықталады. Әрине, тақырып-тамаға осындай көзқарас кезінде оның мүлдем өзге сандық және сапалы қарастырылуы талап етіледі.
56-сурет
5.3 Беттегі нүкте
Қарастырылатын тақырыптамада «Беттегі нүкте» бөлімі өте жауапты болып табылады, өйткені оны меңгеру бетте (нүктелер жиынтығы ретінде) сызықтардың проекцияларын салуға, жалпы және жеке орналасқан жазық-тықтар беттері қимасының фигураларын анықтауға, беттер мен денелерде (сызықтардың жиынтығы ретінде) ойықтар салуға, өз араларында беттердің қиылысу сызықтарын салуға жол ашады. Шешілетін міндеттер шеңберін жай ғана түгендеп кетудің өзі өте анық тұжырымға әкеледі, әрі қарай сызба геометрияда ештеңе жасаудың қажеті жоқ. Сіз бұған көзіңізді жеткізгенше (ал бұл міндетті түрде болады), бұл дәлелге сенуге және төменде баяндалған материалдарға жоғары ынтамен және жауапкершілікпен қарауға кеңес береміз.
5.3.1 Жақты беттер
57-суретте үш жақты пирамиданың үш проекциялы сызбасы берілген. Оған тән бірнеше сәттерді атап кетейік.
57-сурет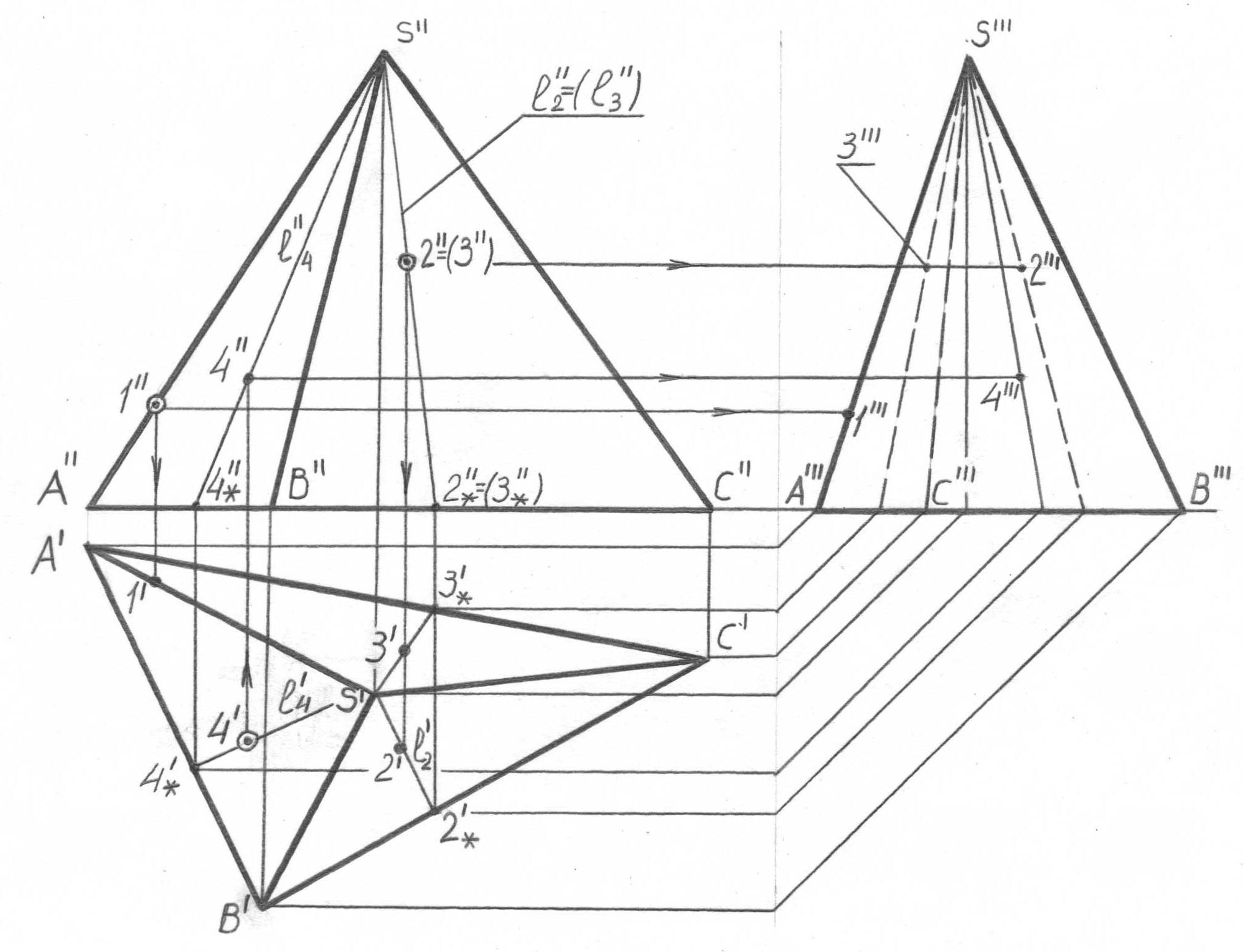
Біріншіден, студент фронталь проекцияда барлық AS, BS, CS қырлары – көрінетін қырлар, бірақ ASC жағы – көрінбейтін, және де AS және CS қырлары фронталь проекция үшін көрінушілік шекаралары болып табылатынын түсіну керек. Профиль проекция үшін AS және BS қырлары - көрінушілік шекара-лары, SC қыры көрінбеушілік шекарасы болып табылады. ASC және BSC көрінбейтін қырлары ASB қырымен жабылған.
Бұл орындар беттің кез-келген жағында орналасқан нүктелердің көрінушілігін анықтайды.
Екіншіден, егер нүкте проекциясы кез-келген қандай да бір қырда беріл-ген болса, оның жетіспейтін проекцияларын осы қырдың сәйкес проекцияла-рынан ғана іздеу керек (параллель проекциялау қасиетін еске түсіріңіз: егер нүкте түзуге тиесілі болса, нүкте проекциялары осы түзудің сәйкес проекция-ларына тиесілі). Фронталь проекцияда берілген 1 нүктесі (1’’ проекциясы) AS қырына (A’’S’’ проекциясы) тиесілі, бұл оның 1’ және 1’’’ горизонталь және профиль проекцияларының осы қырдың A’S’ және A’’’S’’’ проекцияларында орналасқанын бірден анықтайды.
Үшіншіден, пирамиданың кез-келген жағы жазықтықты білдіреді. Онда нүктенің пирамидалық бетке тиесілігіне арналған есеп нүктенің жазықтыққа тиесілігінің белгілі шартына келтіріледі: егер осы жазықтықтың қандай да бір түзуінде жатса, нүкте жазықтыққа тиесілі болады. Пирамиданың бетіне қатыс-ты осындай қандай да бір түзу ретінде құраушыны қабылдаған мақсатқа сәйкес болады, және бұл жағдайда есептің шешімі 53-суретте көрсетілген, жалпы алгоритмге келтіріледі.
Төртіншіден, пирамиданың фронталь және профиль проекцияларында әрбір көрінетін нүктеге көрінетін нүктенің жармасында болатын (бір көру сызығында), көрінбейтін жұп нүкте сәйкес келеді. Сонымен, фронталь проек-цияда 2 - көрінетін нүкте (2’’ проекциясы) 3 – көрінбейтін нүкте (жақшаның ішіндегі 3’’ проекциясы) 2-3 – бір көру сызығында (2’-3’ горизонталь проекции-сы) болады, бірақ олардың әрқайсысы өзінің l2 және l3 құраушысында, сол сияқты бір-бірінің жармасында болатын фронталь проекцияда болады: BSC көрінетін жағының l2 құраушысы ASC көрінбейтін қырының l3 құраушысын жабады (l2’’ = (l3’’)).
Осы сипатты моменттерден алғанда осыған ұқсас түрде (53-суретті қараңыз), мысалы, горизонталь проекцияда берілген 4 - нүктесінің (57-сурет) немесе пирамиданың кез-келген проекциясында берілген, кез-келген басқа нүктенің жетіспейтін проекциялары салынуы мүмкін.
58-суретте үш жақты призма берілген. Мұнда да түйінді моменттерді атап кету керек. Біріншіден, призманың әрбір жағы - горизонталь-проекция-лаушы жазықтықты, ал олардың горизонталь проекциялары, - осы жазықтық-тардың із-проекциялары. Осыдан, кез-келген нүктенің горизонталь проекциясы, ол қайда болса да, осы призманың горизонталь очеркінде ғана орналасуы мүмкін (еске түсіріңіз: проекциялаушы жазықтықта орналасқан, кез-келген нүкте, сызық немесе жазық фигура, оның із-проекциясында көрсетіледі).
Екіншіден, оның жоғарғы қиығында орналасқан барлық нүктелер, горизонталь проекцияда - көрінетін, призманың әрбір жағының кез-келген басқа орнында көрінбейтін болады.
58-сурет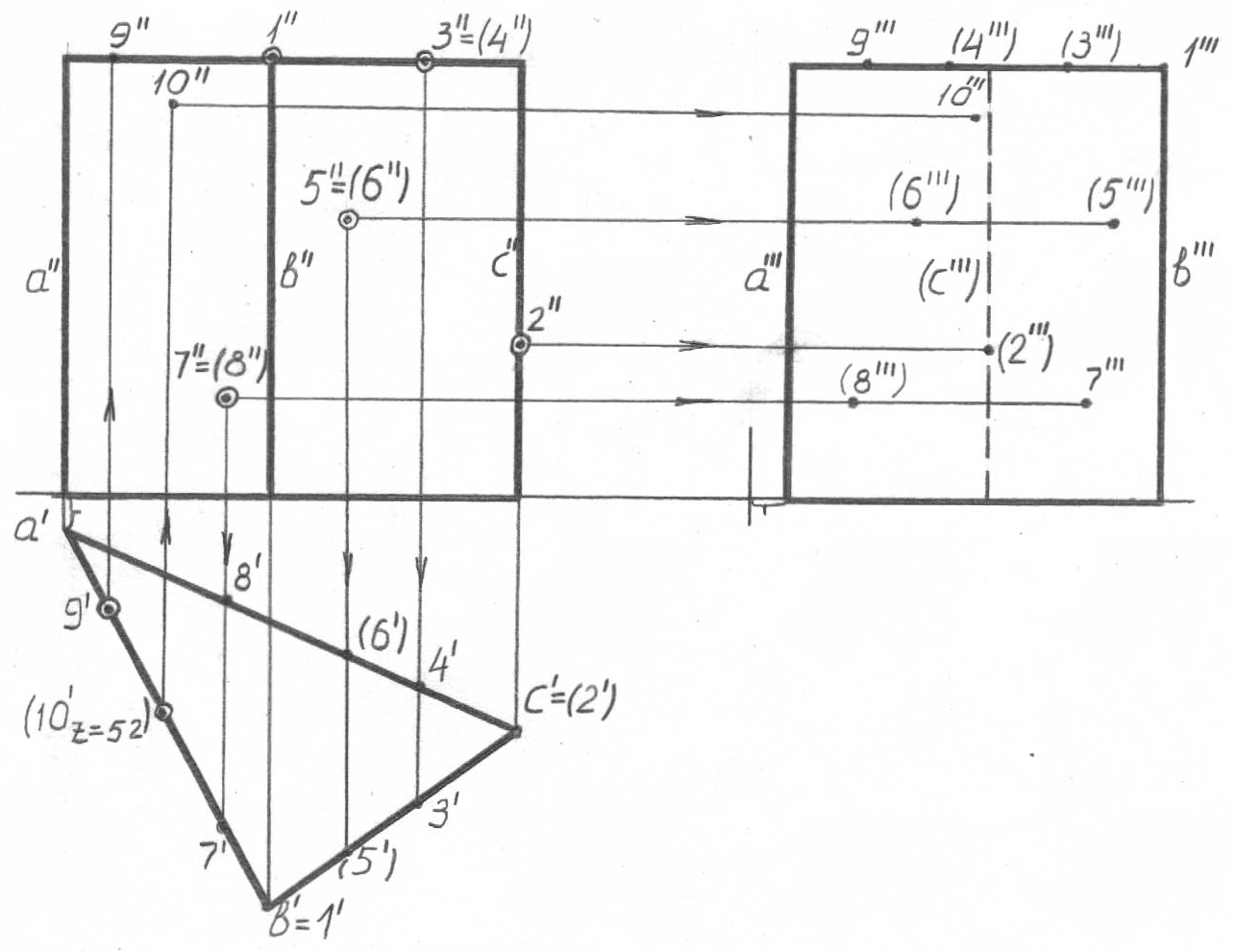
Үшіншіден, жақтары мен олардағы нүктелердің көрінушілігі мәселелері: фронталь проекциядағы ab және bc жақтары – көрінетін, ac жағы – көрінбейтін; профиль проекциядағы ab жағы – көрінетін, ac және cb жақтары – көрінбейтін.
Осыны есепке алғанда b қырының фронталь проекциясының жоғарғы ұшында берілген, 1 нүктесі (1’’- b’’-да орналасқан), призманың басқа проекцияларында көрінетін (1’, 1’’’) және, әрине, b қырының b’, b’’’ сәйкес проекцияларына тиесілі болады. c қырының (2’’ қараңыз) фронталь проекция-сының ортаңғы бөлігінде берілген, 2 нүктесі, қалған проекцияларда (2’, 2’’’) көрінбейтін болады. bc және ac жақтарының жоғарғы қиықтарында берілген, 3 және 4 нүктелері (3’’ және 4’’ қараңыз), горизонталь проекцияда – көрінетін (3’ және 4’ қараңыз), ал профиль проекцияда көрінбейтін ((3’’’) және (4’’’) қара-ңыз) болады, өйткені көрінбейтін қырларда жатыр. Осыған ұқсас түрде 7 және 8 нүктелерінің горизонталь проекциялары, ac жағының W көрінбейтін проек-циясында жатқан, 8 нүктесінің профиль проекциясы сияқты, көрінбейтін болады. Егер горизонталь проекциядағы 9 нүктесі көрінетін ретінде берілсе, онда оның фронталь және профиль проекциялары сөзсіз көрінетін болады. Егер нүктенің горизонталь проекциясы көрінбейтін ретінде берілген болса (10’ қараңыз), онда қосымша ақпаратсыз (мысалы, z = 52) оның тік проекцияларын салу мүмкін емес, бұл беттің толық берілмеуін мүлде білдірмейді.
Қорытындысында тағы да бір жайтты нақтылап кетейік. Беттің, әсіресе симметриялық емес беттің профиль проекциясын салу студенттерде дәстүрлі түрде қандай да бір қиындықтар тудырады. Бұл «нүктені проекциялау» тақыры-бын маңызды меңгермегені туралы, осы материалды тексеру және беттің тіректі сызықтарының ондағы нүктелердің әрбір проекциясын XYZ координа-талары бойынша салу қажеттілігі туралы куәландырады (57-сурет). Инженерлік практикада, тәртіп бойынша, бұл оңай болады: y және z осьтерін көрсетпейді, ал нүктелердің Y мәндерін сызбаны координаталардың басынан құрастыру шарттары бойынша қабылданған, ерікті нүктеден қалдырады (58-сурет, фигура-лы жақша). Айтпақшы, жоғарыда қарастырылған пирамида мен призманың бетіндегі нүктелердің жетіспейтін проекцияларын анықтау бойынша түсініктер сәйкес түрде конустық және цилиндрлік беттер үшін тіпті қолайлы.
5.3.2 Жалпы түрдегі айналым беті
К
59-сурет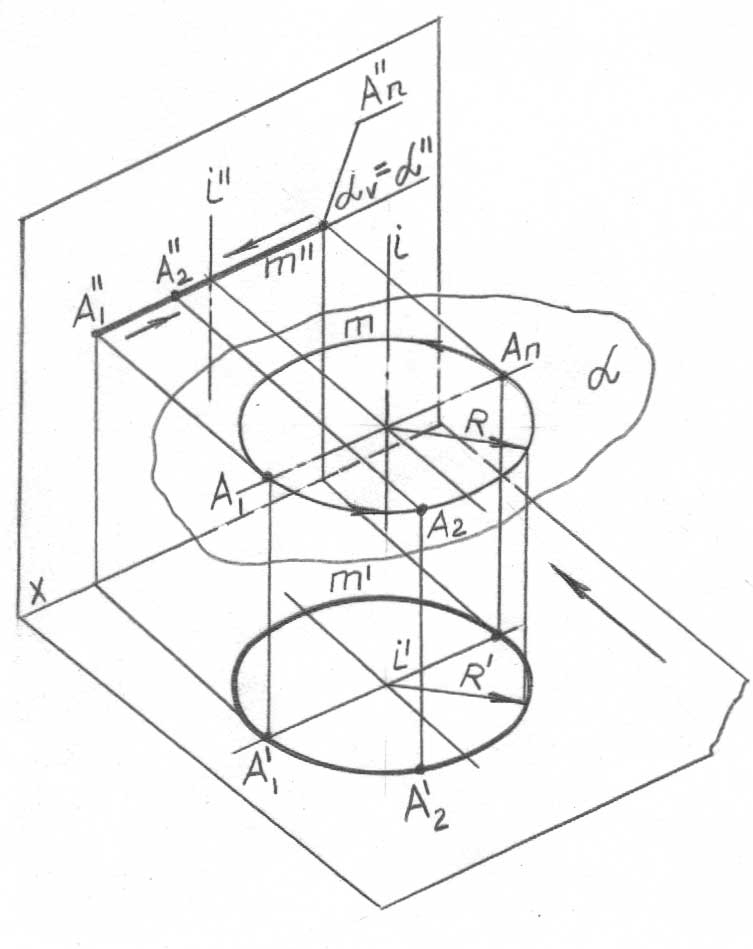
59-сурет
А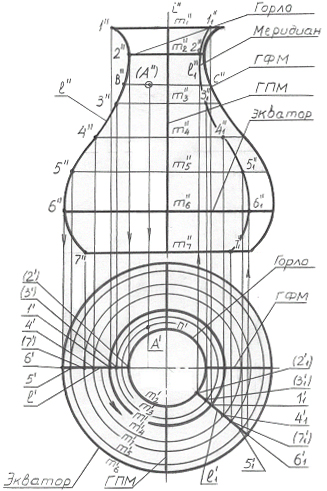 л
енді, i
осінің маңында айналатын нүктелердің
геометриялық орны, бастапқы орнында V
проекцияларының
фронталь жазықтығына параллель, l
ерікті
жазық қисық құраушысы болып табылады
дейік (60-сурет). Оның l’
горизонталь проекциясы дегеніміз х
осіне
параллель түзу. l
құраушысы осьтің
л
енді, i
осінің маңында айналатын нүктелердің
геометриялық орны, бастапқы орнында V
проекцияларының
фронталь жазықтығына параллель, l
ерікті
жазық қисық құраушысы болып табылады
дейік (60-сурет). Оның l’
горизонталь проекциясы дегеніміз х
осіне
параллель түзу. l
құраушысы осьтің
60-сурет
маңайында айналған кезде 1…7 нүктелері, беттің дискретті қаңқасының бір типті сызықтарының жиынтығын білдіретін, m1 … m7 параллельдері бойынша орын ауыстырады. Дискретті қаңқа сызықтарының екінші жиынтығын олардың проекцияларын салу қажет болатын, l1 … lI құраушылары құрайды,. l құраушы-сының горизонталь проекциялары кез-келген қалыпта радиал түзулер, яғни олардың жалғасы i айналу осінің i’ проекциясы арқылы өтетін түзулер болып қалады.
Шеткі оң ln’’ қалпындағы құраушының фронталь проекциясы шеткі сол жақтағы (l’’) құраушының айнадағы кескіні болады. l құраушының кез-келген l1 … ln-1 аралық орны өз траекториясының (өз параллелінің) 1…7 нүктелерінің әрқайсысына m1…m7 (фронталь проекцияда m1’’…m7’’) тиесілігі бойынша l1’ … ln-1’ горизонталь проекциясы арқылы салынады. Басқаша айтқанда, l құрау-шының кез-келген l1 аралық орнының проекцияларын салу үшін қажет:
l құраушының l1’ горизонталь проекциясын жүргізу керек (бұл радиал түзу болады);
оның m1’…m7’ параллельдерінің горизонталь проекцияларымен қиылысуының 11’…71’ нүктелерін табу;
проекциялық байланыс сызықтары бойынша 11’…71’ нүктелерінің проекцияларын m1…m7 параллельдерінің сәйкес m1’’… m7’’ фронталь проекцияларына түсіру (1’ нүктесін m1’’-ге түсіреміз – 11’’ нүктесін аламыз және барлық нүктелер бойынша т.с.с.).
Алынған 1’’…7’’ нүктелері арқылы l1 құраушысының l1’’ фронталь проекциясын жүргіземіз. Сызбаны қарайтпау үшін, онда l құраушының тек бір ғана аралық орны көрсетілген, бірақ осыған ұқсас жолмен олардың нешеуін болса да жүргізуге болады. Сөйтіп, жалпы түрдегі айналу бетінің дискретті қаңқасын салынған деп санауға болады.
Осы беттің дискретті қаңқасының оған тән тірек сызықтарын қарасты-рамыз (60-сурет). Ең кіші диаметрлі параллель «мойын» немесе «қылта» (m2) деп аталады. Ең үлкен диаметрлі параллель экватор (m6) деп аталады. Экватор беттің горизонталь проекциясы үшін көрінушілік аймағының шекарасы болып табылады: горизонталь проекцияда экватордан (және беттің жоғарғы «қайырма-сымен» жабылмаған) жоғары орналасқанның барлығы - көрінетін; горизонталь проекцияда экватордың астында орналасқан нүктелер мен сызықтар көрінбей-тін болып табылады.
Айналу
бетінің i айналу
осі арқылы өтетін жазықтықпен қиылысу
сызығы меридиан
деп аталады. Айналу бетінің бірнеше
меридиандары бар. Проек-циялардың
фронталь жазықтығына параллель меридиан
бас фронталь меридиан деп аталады. Оның
фронталь проекциясы дегеніміз – беттің
фронталь очеркі. Бас фронталь меридиан
фронталь проекция үшін көрінушілік
аймағының шек-арасы болып табылады:
бас фронталь меридианға дейін проекцияның
бетінде орналасқанның барлығы, фронталь
проекцияда - көрінетін (А нүктесін
қараңыз, 60, 61-суреттер), оның одан кейін
орналасқанның барлығы көрінбейтін (В
нүктесі, 61-сурет) болып табылады. Және
ақырында, бас профиль меридиан
проекциялардың профиль жазықтығы үшін
көрінушілік аймағының шекарасы болып
табылады (60-сурет). Оның фронталь және
горизонталь проекциялары –
айналу
осі арқылы өтетін жазықтықпен қиылысу
сызығы меридиан
деп аталады. Айналу бетінің бірнеше
меридиандары бар. Проек-циялардың
фронталь жазықтығына параллель меридиан
бас фронталь меридиан деп аталады. Оның
фронталь проекциясы дегеніміз – беттің
фронталь очеркі. Бас фронталь меридиан
фронталь проекция үшін көрінушілік
аймағының шек-арасы болып табылады:
бас фронталь меридианға дейін проекцияның
бетінде орналасқанның барлығы, фронталь
проекцияда - көрінетін (А нүктесін
қараңыз, 60, 61-суреттер), оның одан кейін
орналасқанның барлығы көрінбейтін (В
нүктесі, 61-сурет) болып табылады. Және
ақырында, бас профиль меридиан
проекциялардың профиль жазықтығы үшін
көрінушілік аймағының шекарасы болып
табылады (60-сурет). Оның фронталь және
горизонталь проекциялары –
61-сурет
бет проекцияларының вертикаль осьтері арқылы өтетін вертикаль түзулер, ал профиль проекциясы беттің профиль очеркімен сәйкес келеді.
5.3.3 Екінші ретті айналу беттері
Екінші ретті айналу беттерін оларға тән барлық ережелерімен және қасиеттерімен бірге жалпы түрдегі айналу бетінің жеке жағдайлары ретінде қарастыруға болады.
5.3.3.1 Сфералық бет
Шеңбер (доға) центрі арқылы өтетін, оське қатысты шеңбердің немесе оның бөлігінің айналуымен құрылады. Осы беттің дискретті қаңқасының тірек сызықтарын қарастырамыз. 62, а-суретте сфераның экваторы және оның проек-циялары көрсетілген. Экватордың горизонталь проекциясы беттің горизонталь очеркімен сәйкес келеді (Экв’=Ф’). Экватордың фронталь және профиль проекциялары сәйкес түрде x және y осьтеріне параллель түзулерді білдіреді. Горизонталь проекциядағы жоғарғы жарты сфера (онда орналасқан барлық нүктелерімен бірге) – көрінетін, төменгі, - көрінбейтін.
62, б-суретте экваторға қосымша түрде ФМ бас фронталь меридиан және оның проекциялары қосымша көрсетілген. Оның проекцияларда орналасуын мұқият зерделеңіз, экватор проекцияларымен салыстырыңыз. ФМ фронталь меридианның ФМ’’ фронталь проекциясының сфераның фронталь очеркімен сәйкес келетінін (ФМ’’=Ф’’), ал оның горизонталь және профиль проекциялары сәйкес түрде x және z осьтеріне параллель түзулер екенін өздеріңіз үшін белгілеп қойыңыздар. Фронталь проекциядағы жақын жарты сфера – көрінетін, алыс – көрінбейтін.
62, в-суретте ПМ бас профиль меридиан және оның проекциялары көрсетілді (қабылдауды ықшамдау үшін экватор және бас фронталь меридиан көрсетілмеген).
ПМ профиль меридианның ПМ’’’ профиль проекциясы беттің Ф’’’ профиль очеркімен сәйкес келеді, ал оның горизонталь және фронталь проекциялары дегеніміз сәйкес түрде x және z осьтеріне параллель түзулер.
62,
а-сурет
62,
б-сурет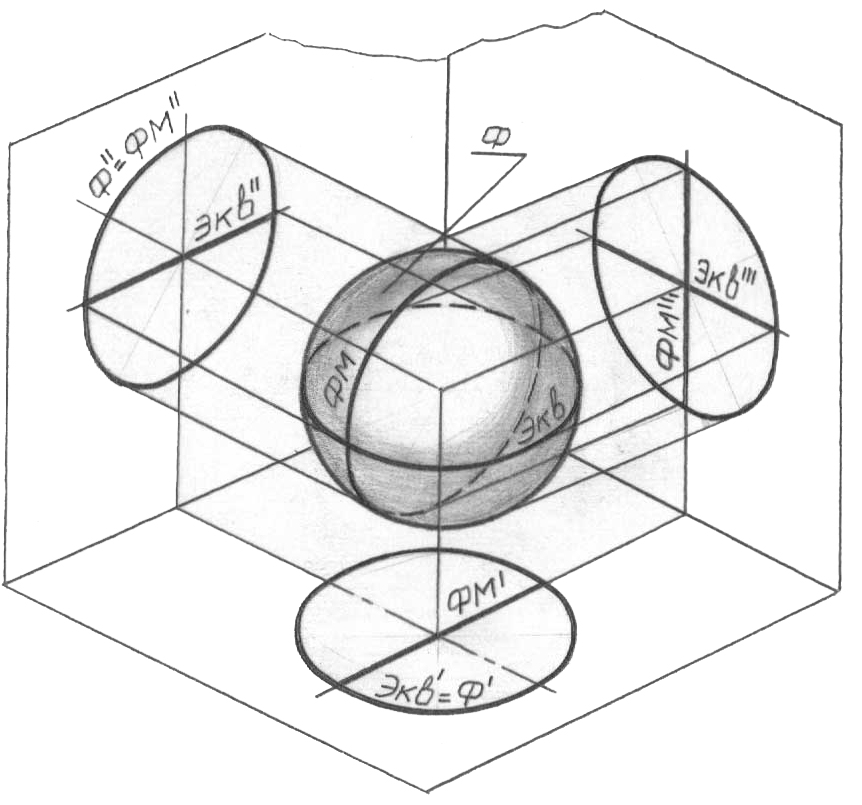
62,
в-сурет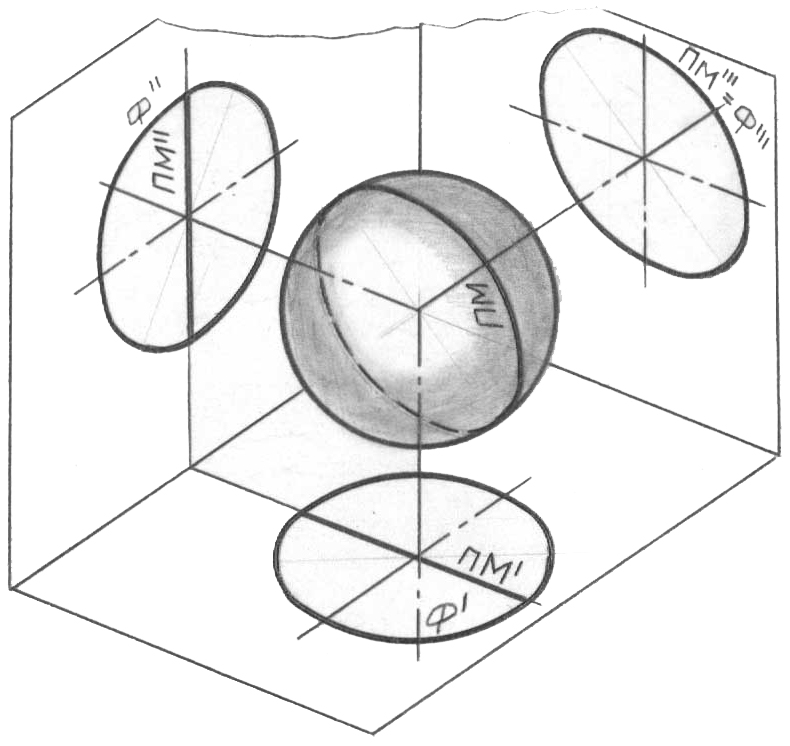
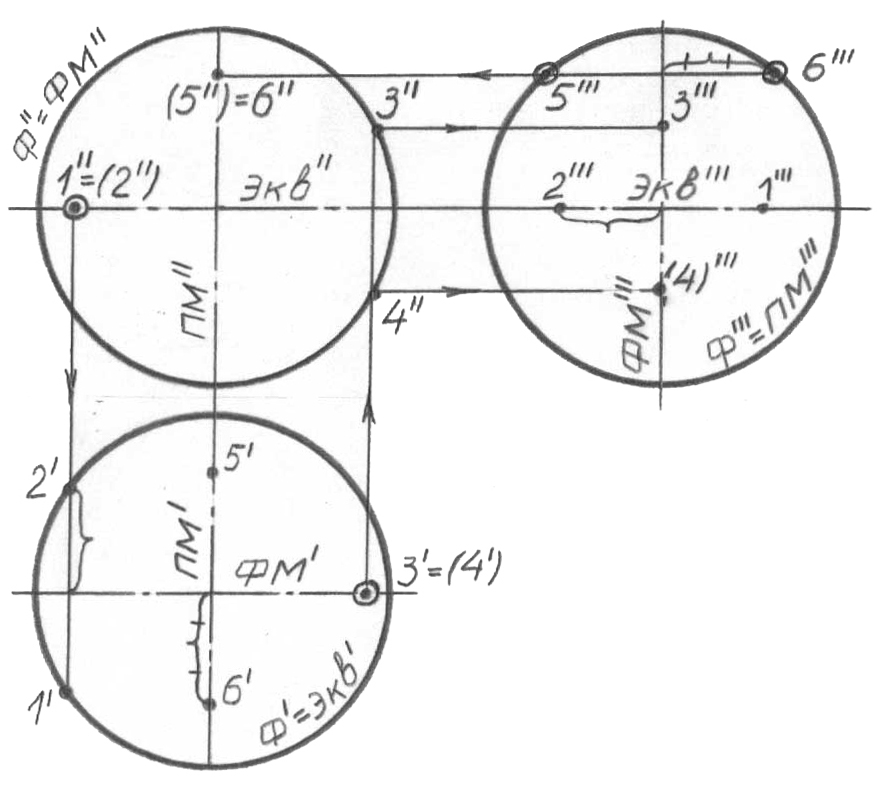
62,
г-сурет
Профиль проекцияның сол жақ жарты сферасы – көрінетін, оң жақ – көрінбейтін.
Ал енді 62, а, 62, б, 62, в-суреттерді 62, г-суретте көрсетілген, бір кескінге ойша жинақтаңыз. Сфералық бет қаңқасының тірек сызықтарының әрқайсысында берілген нүктелердің жетіспейтін проекцияларын, олардың көрінушілігін есепке алғанда, осы тірек сызықтардың сәйкес проекцияларынан іздеу керек. 62, а және 62, г-суреттегі экватордың 1 және 2 нүктелерінің проекцияларын қарастырыңыз да, олардың барабарлығына көз жеткізіңіз. Бас фронталь меридианның горизонталь проекциясында берілген 3, 4 нүктелерді (62, г-сурет) және бас профиль меридианның профиль проекциясында берілген 5, 6 нүктелерін тәртіпке келтіріңіз. Өзіңіздің оқу құралыңызда 62, б, в-суреттегі 3, 4, 5, 6 нүктелерін және олардың проекцияларын (қарындашпен) салуыңызға болады. Оның қаңқасының тірек сызықтарына тиесілі емес сфера нүктелерінің проекциялары, параллельдер проекциялары арқылы жалпы түрдегі айналу бетіне ұқсас түрде анықталады (60, 61-суреттер және оларға берілген мәтін).
