
КІРІСПЕ
Осы дәрістік курс сызба геометрияның теориялық курсын зерделеу үшін негізгі оқу материалы ретінде барлық мамандықтардың және оқу түрлерінің студенттерінің пайдалануы үшін тағайындалған. Оқу құралының тақырыптамасы инженерлік графиканың практикалық курсымен максимум өзара байластыруға бағдарланған және оның теориялық негіздемесі болып табылады. Авторлар материалдың аса қысқа айтылуына және қарапайым баяндалуына ұмтылды, ол үшін орташа және жоғары күрделілікті және толыққан кескіндердің динамикалық (кезең бойынша) модельдерін кеңінен пайдаланды.
Бұрын әзірленгеннің орнына осы оқу құралының жоспарланып отырған электрондық нұсқасы еліміздің басқа жоғары оқу орындарының студенттері үшін де пайдалы болуы мүмкін.
1-БӨЛІМ СЫЗБА ГЕОМЕТРИЯ ПӘНІ.
НҮКТЕНІ ПРОЕКЦИЯЛАУ
1.1 Сызба геометрия пәні
Сызба геометрия (СГ) жазықтықта кеңістіктік объектілерді кескіндеу әдістерін және позициялық, метрлік және конструкторлық есептерді шешу алгоритмдерін зерделейді. Кеңістіктік объектілер деп үш өлшемді, яғни үш өлшемі – ұзындығы, ені және қалыңдығы бар объектілерді түсіну керек. Егер ол шектелген болса, жазықтықтың екі өлшемі бар (ұзындығы және ені). Позициялық есеп – бұл геометриялық объектілердің өзара орналасуын: объектінің артында немесе алдында, оның сол жағында немесе оң жағында, оның жоғарғы немесе төменгі жағында екенін, объектілердің қайсысы – көрінетін, қайсысы көрінбейтін екендігін анықтауға арналған есеп. Метрлік есептер деп кесінділер ұзындықтарын, көлбеу бұрыштарын, жазық фигуралар-ды, аудандарды және т.б. нақты шамаларын анықтауға арналған есептерді түсінуге болады. Осы түсіндірмелердің көмегімен СГ пәнінің бастапқы тұжырымдамасын осылай түсіну керек. СГ – бұл екі өлшемді өлшеуде үш өлшемді объектілерді кескіндеу әдістерін және жоғарыда көрсетілген есептерді шешу тәсілдерін зерделейтін және анықтайтын ғылым.
Енді «конструкторлық есептер» терминін түсіндіру қалды. Конструктор-лық есептер деп графикалық әдістермен берілген, нақты бұйымды ұғыну, кескіндеу және құру бойынша нақты инженерлік шешімдерді қабылдауға арналған есептерді түсіну керек.
СГ негізіне проекциялар, яғни проекциялаушы сәулелердің проекциялар жазықтықтарымен қиылысуымен алынған, проекциялар әдісі салынған.
Аса көп қолданылатын теориялық-көптік символдар және анықтамалар
А, В, С … a, b, c, l, m, n … , , , … Ф1, Ф2, … || . а ,
/
|
- - - - - - - -
-
- - - - |
нүкте; сызық; жазықтық; бет; параллельдік; перпендикулярлық; айқасушылық; «тиесілі», «жатыр» (бірінші таңба – нүктеге қатысты, екінші таңба нүктелер жиыны-на қатысты қолданылады); теріс, қарама-қарсылық таңбасы («емес» терістеуіне балама); объектілердің (жиындардың) қиылысуы; «көрсетеді» (көрсетіледі) «егер …онда»; қайтымдылық («тура және кері пайымдау дұрыс»). |
Символдардың қолданылуын түсіндіретін, бірнеше мысалдарды келтіреміз.
l || m l a b m . n
А l
А l А А
(А l) (А l)
(l m = K) (l m = K) |
- - - -
- - - -
-
-
|
l түзуі m түзуіне параллель. l түзуі m түзуіне параллель емес. a түзуі b түзуіне перпендикуляр. m түзуі параллель емес және n түзуімен қиылыспайды (яғни олар айқасады). А нүктесі l түзуіне тиесілі. l түзуі жазықтығына тиесілі (жатыр) А нүктесі l түзуіне тиесілі емес. А нүктесі А проекциясымен көрсетіледі (басқа-ша айтқанда, А нүктесінің проекциясы дегеніміз А нүктесі). егер А нүктесі l түзуіне тиесілі болса, онда А нүктесінің А проекциясы l түзуінің l проекциясына тиесілі (кері пайымдау ылғи дұрыс болмайды). егер l және m түзулері К нүктесінде қиылысса, онда олардың l және m проекциялары К нүктесінде қиылысады (егер бұл кезде бір мезгілде l m = K шарты орындалса, кері пайымдау дұрыс болады). |
1.3 Проекциялау модельдері
1.3.1 Центрден проекциялау моделі
1.3.1.1 Негізгі терминдер мен анықтамалар (1, а-сурет)
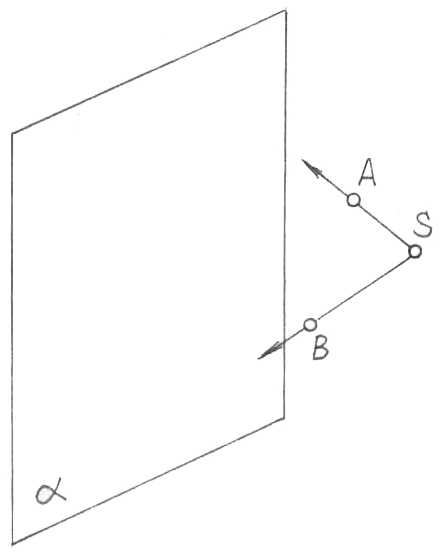

1, а-сурет 1,б-сурет
S А SA В SB SA = A
SВ = В
АВ АВ
= АSB |
- - - - - - -
-
- -
- |
проекциялар жазықтығы; проекциялау центрі; кеңістіктегі нүкте; проекциялаушы сәуле; А ұқсас, кеңістіктегі нүкте; SA ұқсас, проекциялаушы сәуле А нүктесінің жазықтығына центрден проекциясы (1, б-сурет); В нүктесінің жазықтығына центрден проекциясы; кеңістіктегі кесінді (1, в-сурет); АВ кесіндісінің жазықтығына проек-циясы; проекциялаушы жазықтық (проекция-лар жазықтығымен). |
1.3.1.2 Центрден проекциялаудың негізгі қасиеттері
1. Кез-келген нүкте (С, 1, в-сурет), S проекциялау центрінен басқа, өзінің проекциясымен (С) бір мағыналы көрсетіледі.
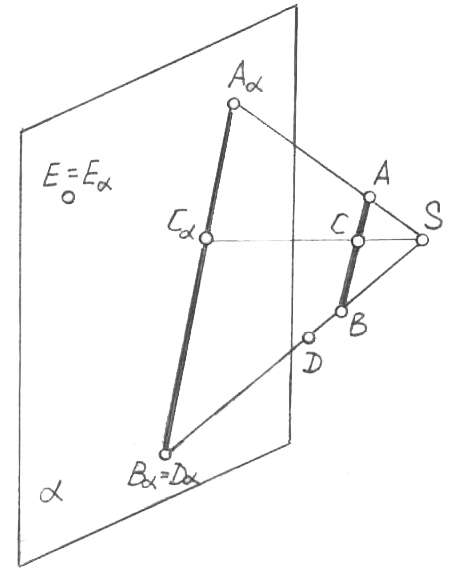
2. Кез-келген проекциялаушы сәуле (SA, SB …) әрбір өзінің нүктесі үшін проекциялаушы болып табылады. Басқаша айтқанда, B, D нүктелері немесе проекциялаушы сәулеге тиесілі, кез-келген басқа нүкте, проекциялары жазықтығында сол және бір орында көрсетіледі (B = D).
3. Проекциялар () жазықтығында жатқан,
1, в-сурет нүктенің (Е) проекциясы, болашақ үлгімен, яғни нүк-
тенің өзімен сәйкес келеді (Е = Е).
4. S проекциялау центрі арқылы өтпейтін түзудің (немесе АВ кесінді-сінің) проекциясы дегеніміз (АВ) түзуі.
1.3.2 Параллель проекциялау моделі
Өзіңізге сұрақ қойыңыз: егер S проекциялау центрін, проекциялар жазықтығынан алысырақ жатқызса, S төбесіндегі бұрыштың шамасымен не болады? (1-сурет). Бұрыштың ара қашықтықтың А-дан -ға дейін ұлғаюына пропорционал азаятыны анық. Ал егер S проекциялау центрін шексіздікке жойса, онда проекциялаушы сәулелер арасындағы бұрыш нөлге тең болады, яғни проекциялаушы сәулелер бір-біріне параллель болады. Сөйтіп, біз параллель проекциялау моделінің мәніне келдік (2-сурет). Егер SA, SB … проекциялаушы сәулелері өз араларында параллель болса және проекциялар жазықтығына перпендикуляр болмаса, онда параллель қисық бұрышты проекциялау моделі орын алады. Егер SA, SB … проекциялаушы сәулелері өз араларында параллель болса және проекциялар жазықтығына перпендикуляр перпендикуляр болса, модель параллель ортогональ проекциялау моделі деп аталады. Осы модель барлық СГ, инженерлік графиканың және өнеркәсіптегі конструкторлық қызметтің негізі болып табылады. Параллель ортогональ проекциялау моделіне қатысты кейбір негіз құраушы сәттерді тұжырым-даймыз.
Н
2-сурет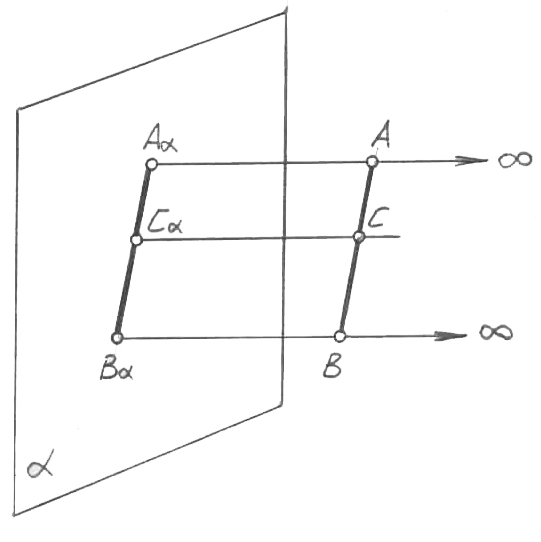
Графикалық ақпараттың жалғыз тәсілі ретінде сызбаға келесі талаптар қойылады: көрнектілік, қарайымдылық, өлшемдерді оқу ыңғайлылығы және қайтымдылық. Қайтымдылық деп кері есепті шешу – заттың проекцияларын (минимум санын) оның көрнекті кескінделуі бойынша салу сияқты, оның проекциялары бойынша бір мәнді және толық түсіну мүмкіндігін түсіну керек.
1.3.3 Параллель проекциялау инварианттары
Инварианттар деп өзгермейтін қасиеттерді, оларда барлық СГ және ИГ негізделетін, графикалық аксиомаларды түсінуге болады. Олардың негізгілерін атап өтейік.
Нүктенің проекциясы дегеніміз нүкте.
Проекция
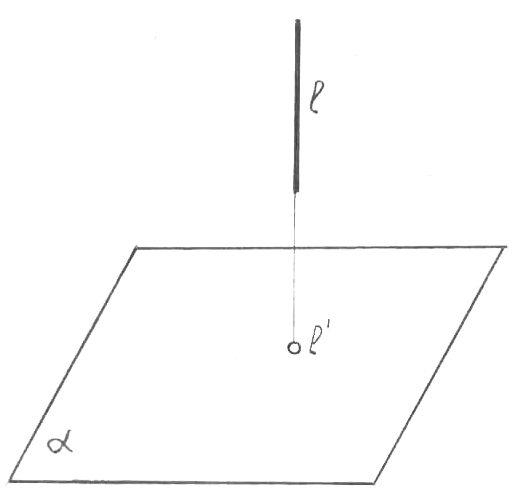 лар
жазықтығына перпендикуляр емес түзудің
проекциясы дегеніміз түзу. Егер түзу
проекциялар жазықтығына перпендикуляр
болса, онда оның осы жазықтыққа проекциясы
дегеніміз нүкте (3-сурет).
лар
жазықтығына перпендикуляр емес түзудің
проекциясы дегеніміз түзу. Егер түзу
проекциялар жазықтығына перпендикуляр
болса, онда оның осы жазықтыққа проекциясы
дегеніміз нүкте (3-сурет).Егер нүкте (С, 2-сурет) түзуге (АВ кесіндісі) тиесілі болса, онда осы нүктенің (С) проекциясы осы түзудің (АВ) проекциясына тиесілі.
Проекция
3-сурет
лар жазықтығына параллель түзудің кесіндісі, оған нақты шамаға
проекцияланады.
Параллель түзулер проекциялары параллель (немесе сәйкес келмейді).
Параллель кесінділер ұзындықтарының қатынасы олардың проекция-лары ұзындықтарының қатынасына тең.
Егер нүкте (С, 2-сурет) кесіндіні қандай да бір қатынаста бөлсе (мысалы АС:СВ = 1:2), онда (С) нүктесінің (С) проекциясы кесінді-нің (АВ) проекциясын сол қатынаста бөледі (АС : СВ = 1 : 2).
Егер түзулер кеңістікте қиылысса, онда олардың проекциялары да қиылысады, және де проекциялардың (С, 4-сурет) қиылысу нүктесі дегеніміз болашақ үлгілер (l және m сызықтары) қиылысуының (С) нүктесінің проекциясы.
О
4-сурет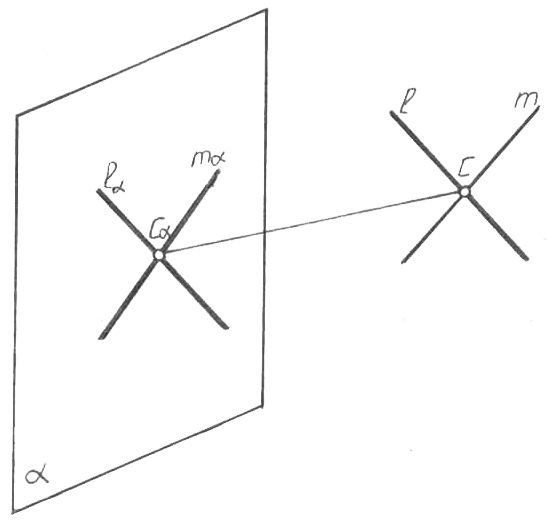
нуға келтіріледі.
1.4 Проекциялардың екі жазықтығы жүйесіндегі нүкте. Г. Монж эпюрі
Проекциялау әдісімен кескіндерді салу идеясы оларға объект проекция-ланатын жазықтықтар жүйесінің бар болуын болжайды. Элементар геомет-риялық объектіні – екі өзара перпендикуляр жазықтықтар жүйесіндегі нүктені қарастырамыз (5-сурет). Проекциялар жазықтықтары, жазықтықтар сияқты - геометриялық проекциялау объектілері, СГ-да шексіз, көрінбейтін және шексіз жұқа болып саналады. Ал олай болса, кескіндердегі жазықтықтар қандай да бір сызықтармен жасанды шектеледі.
Проекциялардың екі өзара перпендикуляр жазықтықтары: Н – горизон-таль және V – фронталь, х осі бойымен қиылысып, кеңістікті 4 ширекке бөледі. Біз бірінші ширекте тұрған және одан (проекциялардың әрбір жазықтығынан) шексіз алыстатылған болып есептеледі, 5-сурет.
5-сурет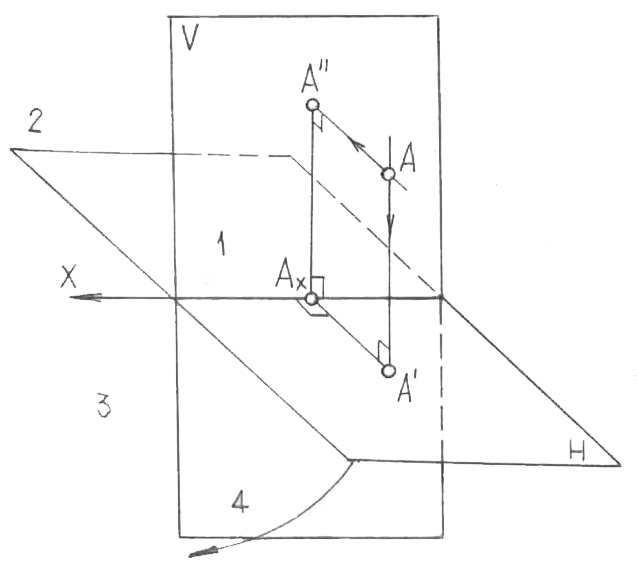
А – кеңістіктегі нүкте;
А’ – А нүктесінен Н проекцияларының горизонталь жазықтығына түсірілген перпендикулярдың негізі, яғни А’ – А нүктесінің горизонталь проекциясы. Осыған ұқсас, А’’ – А нүктесінің фронталь проекциясы. АА’ = А’’Аx екенін көру қиын емес – бұл нүктеден Н проекцияларының горизонталь жазықтығына дейінгі ара қашықтық. Нүктені және оның проекцияларын осылай кескіндеу (және қабылдау) кез-келген студенттің қолынан келеді. Алай-да, егер бірнеше нүктелердің (немесе бірнеше ондаған нүктелердің) жиын-тығын білдіретін объект туралы сөз болса, мұндай кескін көп еңбек етуді қажет етіп қана қоймай, сонымен бірге проблемалы болады.
Сызба
геометрияның негізін құраушы болып
саналатын, француз геометрі Гаспар
Монж, объектілерді кескіндеудің
принциптік жаңа (өз уақыты бойынша)
әдісін: Н
горизонталь проекциялар жазықтығын х
осінің маңында фронталь жазықтықтар
проекциясымен бірлестіргенге дейін
бұруды ұсынды. Сонымен бірге (6, а-сурет)
АхА’
сызығы х
осіне перпендикуляр А’’Ax
сызығының
жалғасы болып табылады.
А нүктесі болмайтындай, жоғалып кететіндей
сияқты, бірақ екі жазықтықты кеңістікте
нүктенің орналасуын бір мағыналы
анықтайтын, оның А’
және A’’
проекциялары
қалады. V
және Н
проекцияларының жазықтықтарын
контурлайтын сызықтар,
 таза шартты сипатта болатындықтан
(жазықтықтар шексіздігінен), оларды
ешбір ақпараттық мағынасын жоғалтпай
алып тастауға болады. Қорытындысында
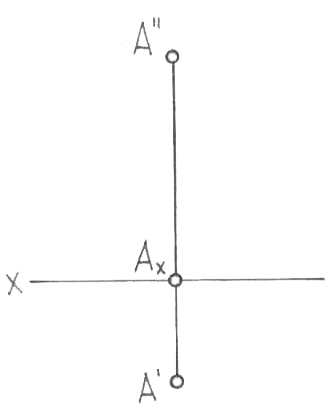
6, б-суретте көрсетілген және Г. Монж
эпюрі деп аталатын, мәні бойынша екі
жазықтықты жүйедегі А
нүктесінің сызбасы болып табылатын, А
нүктесінің кескіні шығады. СГ және ИГ
пәнінің ерекшелігі де осында: объект
проекциялары бойынша
таза шартты сипатта болатындықтан
(жазықтықтар шексіздігінен), оларды
ешбір ақпараттық мағынасын жоғалтпай
алып тастауға болады. Қорытындысында
6, б-суретте көрсетілген және Г. Монж
эпюрі деп аталатын, мәні бойынша екі
жазықтықты жүйедегі А
нүктесінің сызбасы болып табылатын, А
нүктесінің кескіні шығады. СГ және ИГ
пәнінің ерекшелігі де осында: объект
проекциялары бойынша
6, а, б-сурет
графикалық объектінің өзін: оның кеңістіктегі орнын, пішінін, геометриялық қасиеттерін және т.б. мүлдем бір мағыналы және толық «оқу».
1.5 Проекциялардың үш жазықтығы жүйесіндегі нүкте
Жоғарыда қарастырылған екі жазықтықты нүкте, үш өлшемді әлемнің геометриялық қасиеттерін толық шамасында көрсете алмайды. Сондықтан СГ және ИГ-да проекциялардың үш өзара перпендикуляр жазықтығына (7-сурет): фронталь V, горизонталь H және профиль W проекциялау негіз құраушы болып табылады, олар 0 координаталар басынан шығатын, х абсциссалар, у ордината-лар және z аппликаталар осьтері бойымен қиылысады. Проекциялардың үш жазықтығы жүйесінің кеңістікті октанттар деп аталатын, 8 бөлікке бөлетінін байқау қиын емес. Бақылаушы бірінші октанта орналасқан және проекциялар жазықтықтарынан шексіз алыстатылған болып саналады.
А ерікті нүктесін және оның осы жүйедегі проекцияларын қарастырамыз. А’ және А’’ – алдыңғыға ұқсас (6-сурет), А нүктесінің сәйкес түрде горизонталь және фронталь проекциялары. А’’’ – А нүктесінің профиль проекциясы. А нүктесінен проекциялардың профиль жазықтығына дейінгі АА’’’ ара қашық-тығы Х=ОАх абсциссасымен анықталады. Осыған ұқсас, А нүктесінен проекциялардың V фронталь жазықтығына дейінгі АА’’ ара қашықтығы - Y = A’Ax ординатасымен, ал проекциялардың Н горизонталь жазықтығына дейінгі ара қашықтық Z=AA’ =AxA’’ аппликатасымен анықталады. Нүктенің кеңістікте орналасуын бір мағыналы анықтайтын, 0АхА’А сынық сызығы,
7-сурет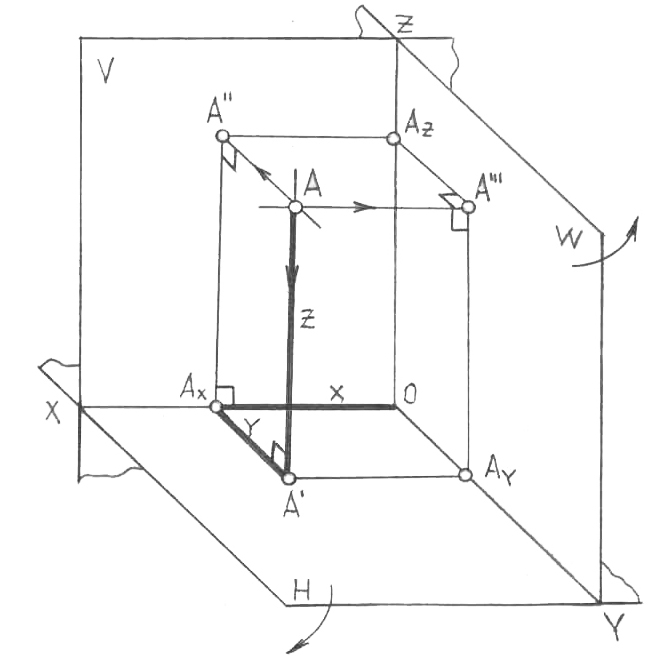
координаталық сынық сызық деп аталады, ол бойынша проекциялардың үш жазықтығы жүйесінде нүктенің сұлбасы салынады (кешенді сызба). Ол үшін, алдыңғы жағдайдағыдай, проекциялардың Н горизонталь жазықтығы х осінің маңында фронталь жазықтықпен бірлескенге дейін, ал W профиль жазықтығы, z осінің маңында, тағы да проекциялардың V фронталь жазықтығының жалғасымен бірлескенге дейін бұрылады. Сонымен бірге ось бойлай жарыла-тын және екі – 0 координаталар басынан төмен қарай және одан оңға қарай (8, а-сурет) орынды алатын сияқты; A’Ax - A’’Ax жалғасы, ал A’’’Az – A’’Az жалғасы болады. A''AxA’, A’’AzA’’’ және A’AyA’’’ сызықтары проекциялық байланыс сызықтары деп аталады және нүктенің кешенді сызбасын салу үшін - тірек сызықтар, ал координаталық сынық сызықтың параметрлері оның негізі болып табылады.
Тағы бірнеше маңызды моменттерді атап кетейік. Біріншіден, 7 және 8, а-суретте координаталық осьтердің тек оң бағыттары ғана көрсетілген, бірақ олардың әрқайсысына 0 координаталар басынан қарама-қарсы жаққа өзінің теріс бағыты сәйкес келеді. H және W жазықтықтарын бұрған соң олардың орналасуы осьтердің оң бағыттарымен сәйкес келеді және 8, а-суретте жақшаның ішінде көрсетілген.
Е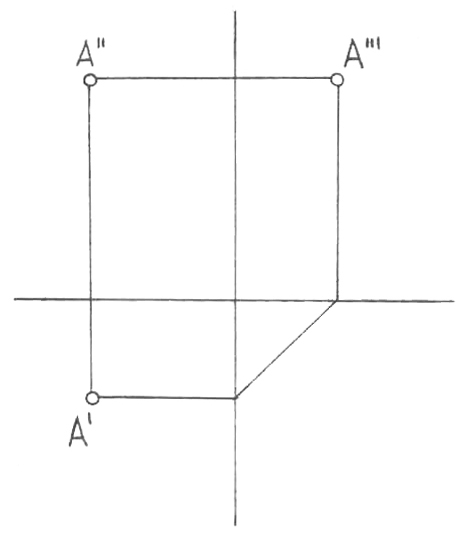 кіншіден,
кез-келген екі проекцияда координаталық
қисық сызықтың барлық X,
Y,
Z
үш координатасы бар. Бұдан мынадай
маңызды тұжырым шығады: кеңістікте
нүктенің орналасуы оның кез-келген екі
проекциясымен мүлдем бір мағыналы
анықталады. Ал бұдан тағы бір маңызды
тұжырым
кіншіден,
кез-келген екі проекцияда координаталық
қисық сызықтың барлық X,
Y,
Z
үш координатасы бар. Бұдан мынадай
маңызды тұжырым шығады: кеңістікте
нүктенің орналасуы оның кез-келген екі
проекциясымен мүлдем бір мағыналы
анықталады. Ал бұдан тағы бір маңызды
тұжырым
8, а-сурет
8, б-сурет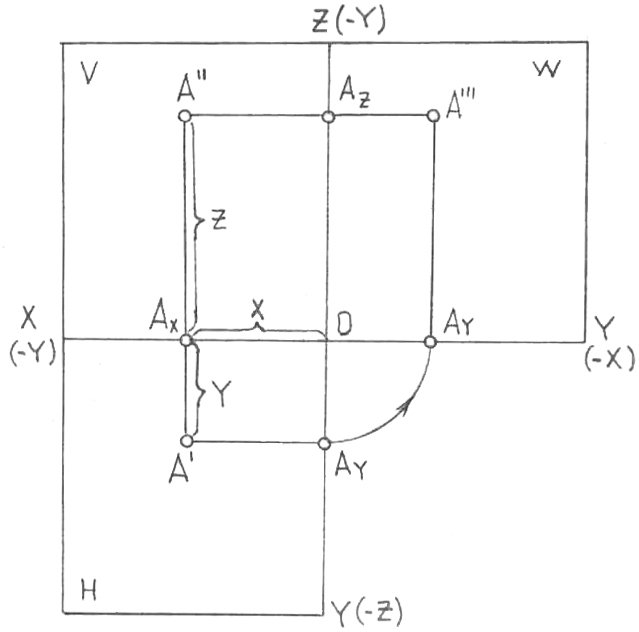
шығады: нүкте, түзу және жазықтық сияқты элементар геометриялық объекті-лер және олардың жиынтықтары үшін, есептерді шешуді екі жазықтықты кескіндерге келтіру керек.
Үшіншіден, проекциялардың осьтері мен жазықтықтарының орналасуы және белгіленуі өзгеріссіз болатындықтан, ал AxAyAz нүктелері салудың қосымша элементтері болып табылатындықтан, оларды кейін қажет болмаса кешенді сызбада көрсетудің керегі жоқ. Сонда кешенді сызба 8, б-суретте көрсетілген түрді түпкілікті қабылдайды.
Оның салынуы жалпы жағдайда келесі тәртіпте жүргізілу керек. x осінің бойында X абсциссаның берілген мәні салынады, Ах нүктесі көрсетіледі (бірақ белгіленбейді). Ол арқылы х осіне перпендикуляр, проекциялық байланыс сызығы жүргізіледі. Онда төмен қарай – Y ординатасының берілген мәні, (А нүктесінің А’ горизонталь проекциясы алынады), ал жоғары қарай Z аппликата-сының берілген мәні салынады (А нүктесінің A’’ фронталь проекциясы алынады), сызба дайын. Қажет болғанда А нүктесінің үшінші проекциясы жоғарыда сипатталған тәсілмен (8, а-сурет) салынады.
Нүктені проекциялаудың мәнін аса терең түсіну үшін студенттерге, нөлден ерекшеленетін координаталардың, координаталардың біреуі нөлге тең болғанда V, H, W проекциялары жазықтықтарының әрқайсысында орналасқан нүктелердің және екі координата нөлге тең болғанда, х, y, z осьтерінің әрқайсы-сында орналасқан нүктелердің нақты мәндері бар нүктелердің сызбаларын өз бетімен салу ұсынылады. Әрбір мысалда нүктенің үш проекциясын (мысалы A’, A’’, A’’’) және егер Сіз оларсыз сызу қиын болса, қосымша нүктелерді (Ах, Ay, Az) белгілеу керек.


 ||
m
||
m