1.2.6 Производные сложных функций

Приведенные в предыдущем параграфе правила и формулы дифференцирования позволяют находить производные от функций только в самых простых случаях. Знания этих правил и формул недостаточно для дифференцирования функций более сложного вида, таких, например, как или . В подобных случаях пользуются более общими формулами дифференцирования, основанными на теореме о производной функции от функции.

Пусть у есть функция от и: у =f (и), где и, в свою очередь функция от аргумента х: и = φ (х); в таком случае говорят, что у есть функция от функции. Очевидно, можно записать у = f (φ (x)). Если существуют и производные = (u) и = φ'(х), то существует и производная от y по х, причем имеет место равенство

. (1.40)

Индексы указывают, по какой переменной производится дифференцирование. Покажем, как пользоваться формулой (1.40).

Задача 1.14

Найти y' , если _у = (х²+5х + 7)⁸.

Полагая u = х² + 5х+7, имеем y= u⁸.

По формуле(3) y' = 8u⁷(2х+5), или окончательно

y' = 8(х² + 5х+7)⁷ (2х+5).

Задача 1.15

Найти y', если у = ln(х³ +7х + 2).

Принимая в данном случае за и = х³ +7х + 2 и пользуясь формулой (10), получаем

.

Многие физические величины определяются как производные по времени от других физических величин. Например, скорость — первая производная радиус-вектора по времени t. Обозначается это следующим образом:

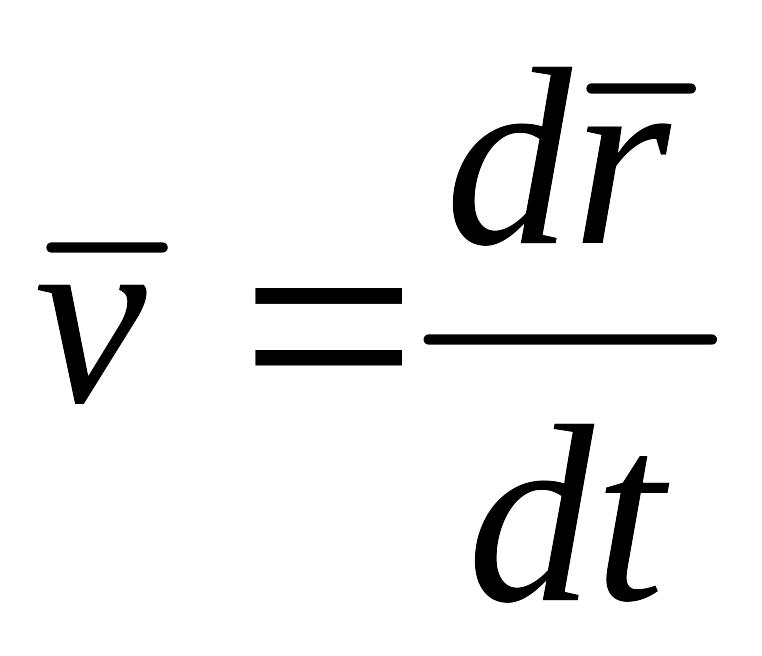или . (1.41)

Ускорение - первая производная скорости по времени t

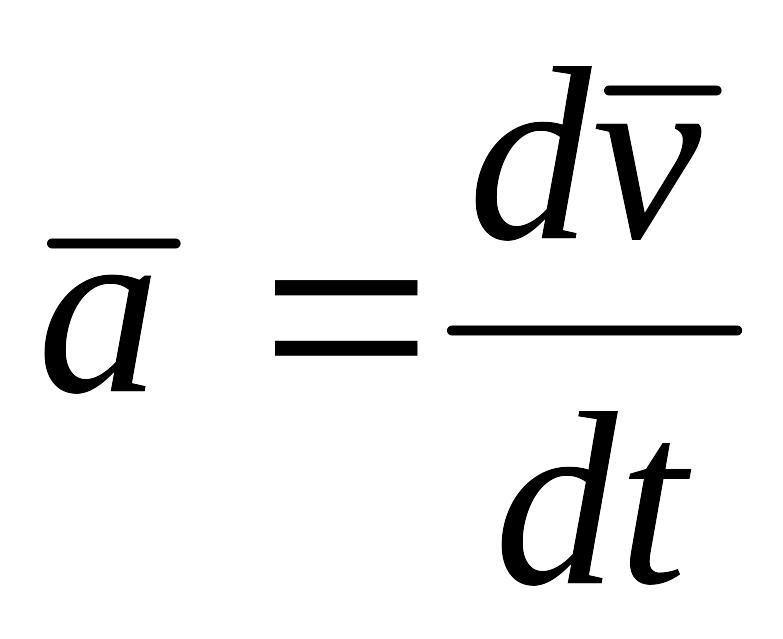или . (1.42)

Примеры решения задач

Задача 1.16

Радиус-вектор материальной точки меняется со временем по закону , м. Найти: 1) зависимость скорости точки от времени (t), 2) зависимость модуля скорости от времени (t), 3) зависимость ускорения точки от времени (t), 4) зависимость модуля ускорения от времени а (t), 5) значения скорости и ускорения в момент времени t= 1 с от начала движения.

Дано: , м; t= 1с.

Найти: (t),v(t), (t),a(t),v, а.

Решение. 1. Скорость — первая производная радиус-вектора по времени. Поэтому для нахождения зависимости (t) достаточно продифференцировать по времени заданную зависимость :

, м/с. (1)

2. Модуль вектора определяется по теореме Пифагора как корень из суммы квадратов компонент вектора. Для модуля скорости

.

Из уравнения (1) имеем v_x = 4t м/с, v_y = 3 м/с, v_z = 0 м/с.

Получаем

, м/с (2)

3. Так как ускорением является первая производная скорости по времени, то для получения зависимости от t необходимо продифференцировать по времени полученную выше зависимость выражение (1). Тогда

= , м/с². (3)

4. Модуль ускорения определяется соотношением . Как видно из зависимости (3), а_х = 4 м/с², а_у = 0 м/с², а_z = 0 м/с². Поэтому

= 4 м/с². (4)

5. Значения скорости и ускорения в момент времени t = 1 с от начала движения легко получить, подставив значение времени t = 1 с в выражения (2) и (4). Тогда v (1) = 5 м/с, а (1) = 4 м/с².

Ответ: зависимость скорости точки от времени = , м/с;

зависимость модуля скорости от времени , м/с;

зависимость ускорения точки от времени , м/с²;

зависимость модуля ускорения от времени a(t) = 4 м/с²;

значения скорости и ускорения в момент времени t = 1 с от начала движения: v (1) = 5 м/с, а (1) = 4 м/с².