1.1.9 Выражение скалярного произведения через координаты сомножителей

Если известны координаты двух векторов = {а_х1, a_yl, a_zl} и

= {а_х2, а_у2, а_z2}, то скалярное произведение этих векторов

. (1.18)

Примеры решения задач

Задача 1.10

Найти длины векторов = {3, 2, 1} и = {2, -3, 0} и их скалярное произведение.

Дано: = {3, 2, 1}; = {2, -3, 0}.

Найти: , , _.

Решение. Искомые длины

,

,

.

Значит, векторы и перпендикулярны.

Ответ: , , скалярное произведение = 0.

Задача 1.11

Найти угол α между векторами = {-2, 1, 2} и = {-2, -2, 1}.

Дано: = {-2, 1,2}; = {-2,-2, 1}.

Найти: .

Решение. Длины векторов

, .

Скалярное произведение

=(-2).

Так как ,

то , т.е. .

Ответ: угол между векторами α ≈ 63°37'.

1.1.10 Векторное произведение двух векторов

Векторным произведением вектора (множимое) на непараллельный с ним вектор (множитель) называется третий вектор (произведение), который определяется следующим образом:

1) модуль численно равен площади параллелограмма (AOBL на рис. 1.19), построенного на векторах и

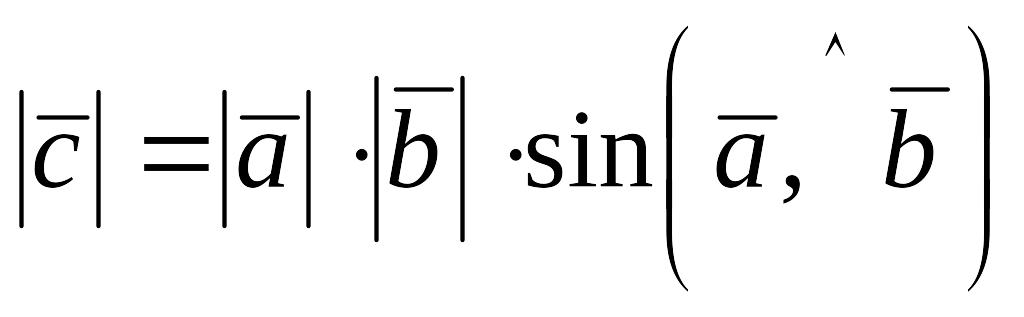. (1.19)

2) линия, вдоль которой направлен вектор , перпендикулярна плоскости упомянутого параллелограмма;

Рис. 1.18

3) направление вектора выбирается так, чтобы векторы , и составляли правую систему, т. е. вектор направлен в такую сторону, из которой переход вращением от первого вектора — сомножителя ко в торому вектору-сомножителю через наименьший угол виден против хода часовой стрелки.

Обозначения: . (1.20)

1.1.11 Выражение векторного произведения через координаты сомножителей

Если известны координаты двух векторов = {а_х, a_y, a_z} и

= {b_х, b_у, b_z}, то векторное произведение этих векторов

= (a_yb_z - a_zb_y) + (a_zb_x - a_xb_z) + (a_xb_y-a_yb_x) . (1.21)

1.1.12 Физический смысл векторного произведения

В механике многие величины определяются как векторное произведение других величин.

1. Так, моментом силы относительно неподвижной точки О называется вектор , равный векторному произведению радиус-вектора , проведенного из точки О

в точку приложения силы, и вектора силы :

(1.22)

На рисунке 1.18 векторы и лежат в горизонтальной плоскости, а вектор момента силы перпендикулярен плоскости перемножаемых векторов и направлен вверх.

2. Моментом импульса относительно неподвижной точки О называется вектор , равный векторному произведению радиус-вектора , проведенного из точки О к материальной точке, обладающей импульсом

. (1.23)

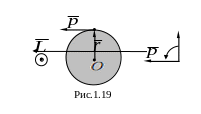На рисунке 1.19 показано, что тело движется по окружности против часовой стрелки. Так как импульс , где т — масса тела, - его скорость, он, как и вектор , направлен по касательной к траектории. По правилу векторного произведения двух векторов и результирующий вектор лежит в плоскости, перпендикулярной плоскости перемножаемых векторов, и направлен на нас, так как векторы , , составляют правую систему.