П.1.1 Степени и корни

Степень числа а определяется при п натуральном равенством

,

где число множителей в правой части равенства равно п.

Корень степени п определяется равенством . Далее принимается:

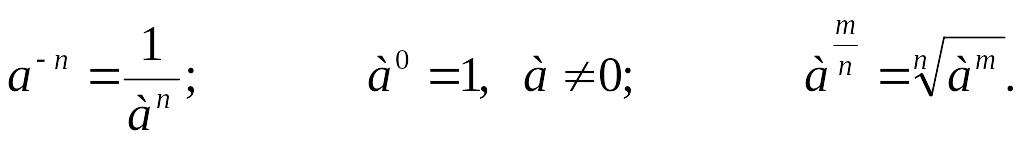
При любых показателях справедливы следующие формулы:

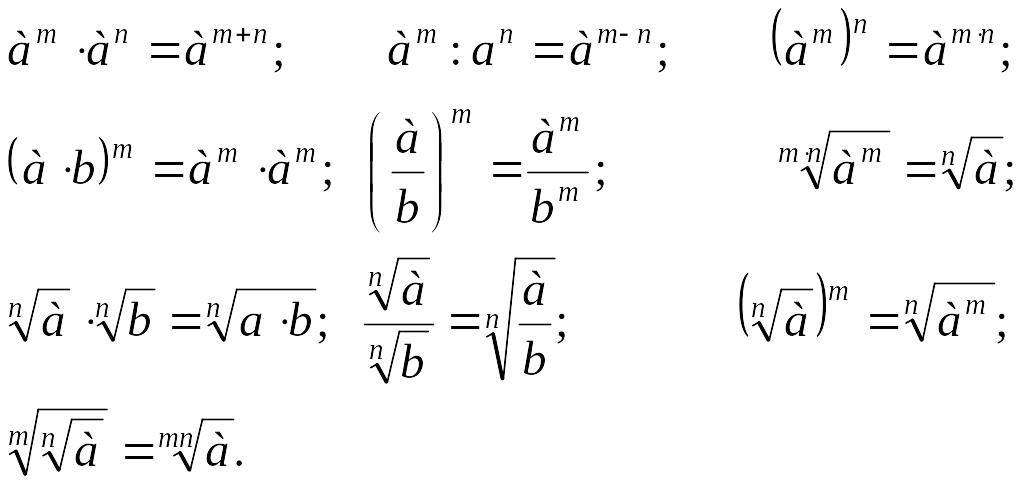
Формулы сокращенного умножения и деления:

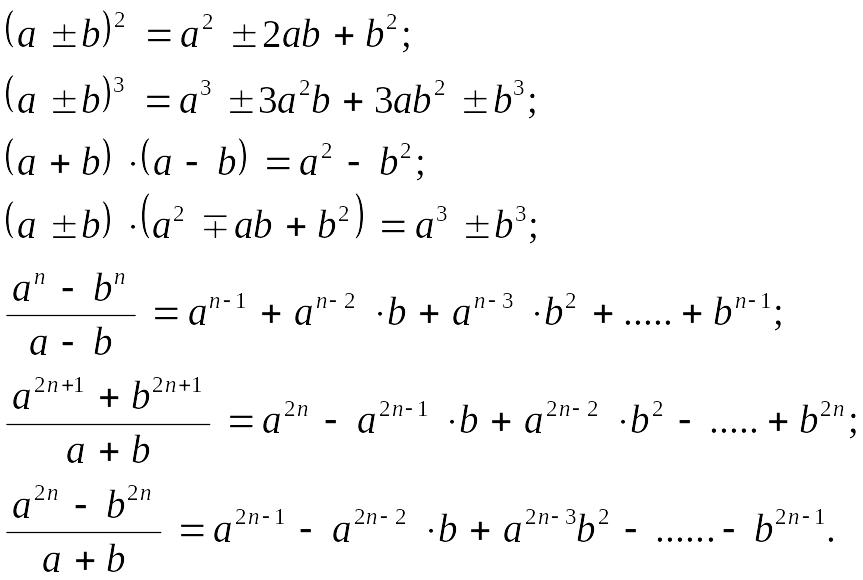
Примечание. В приведенных формулах предполагается, что знаменатели отличны от нуля, а иррациональные величины являются действительными числами.

П.1.2 Логарифмы

Если где и , то показатель п называется логарифмом числа N при основании а; обозначение: п = log_aN, или п = lg_aN. Всякое положительное число имеет логарифм.

Основные формулы:

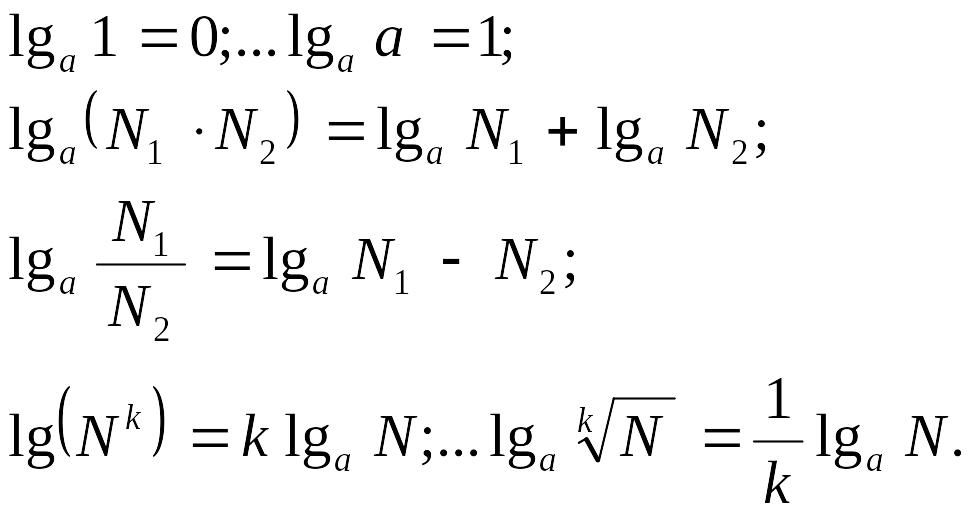
Употребительны две системы логарифмов: десятичные, для них основанием является число 10 (обозначение lgN); натуральные, для них основанием является число е (обозначение lnN),

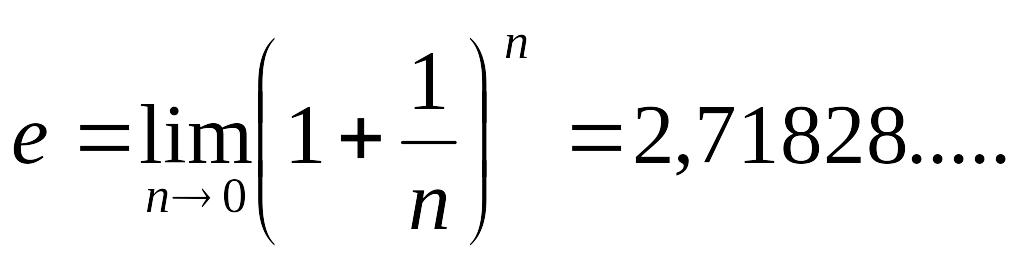
При основании а>1 имеют место следующие свойства:

большему числу соответствует больший логарифм;

логарифмы чисел, меньших единицы, отрицательны;

логарифмы чисел, больших единицы, положительны;

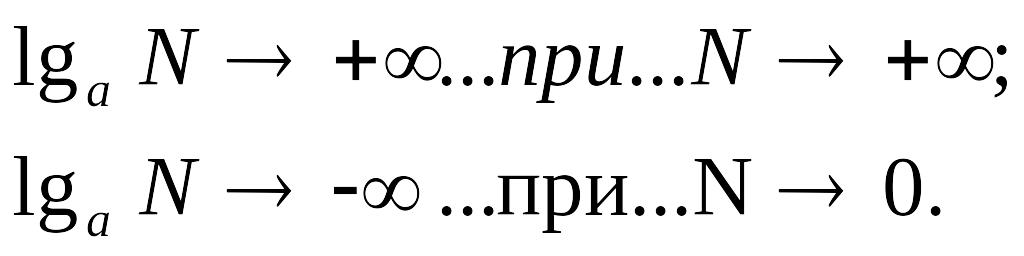
Г рафик логарифмической функции при а>1 дан на рис. П.1.1.

Десятичный логарифм числа состоит из целой части, называемой характеристикой, и дробной части, называемой мантиссой. Характеристика числа, большего единицы, на единицу меньше числа его цифр, стоящих левее запятой; характеристика числа, меньшего единицы, отрицательна и равна по модулю числу нулей, стоящих левее первой значащей цифры, включая нуль целых.

Например, характеристика логарифма числа 25,3 равна 1, а числа 0,00253 равна - 3.

Логарифмы числа при двух различных основаниях связаны соотношением

в частности

число называется модулем перехода от основания, а к основанию b. Между десятичными и натуральными логарифмами соотношение таково:

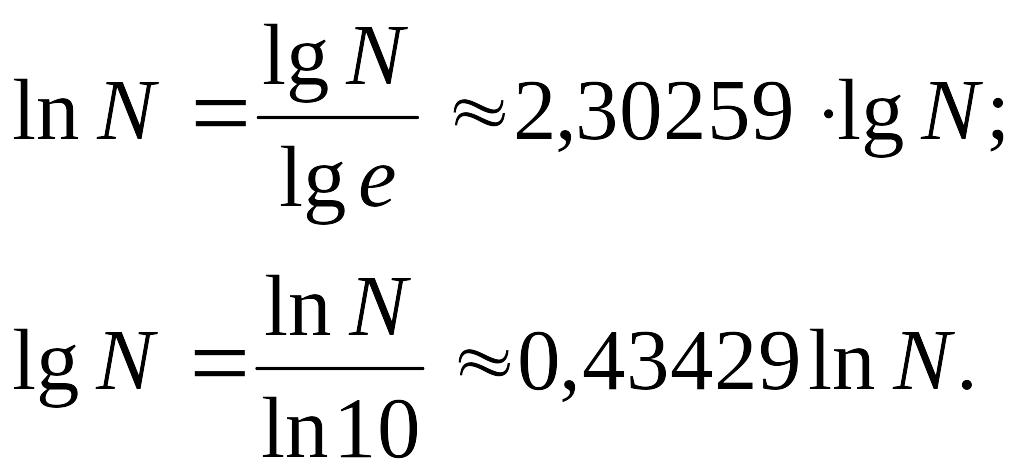
П.1.3 Прогрессии

Арифметической прогрессией называется ряд чисел, в котором каждое последующее число получается прибавлением к предыдущему одного и того же числа, называемого разностью прогрессии. Геометрической прогрессией называется ряд чисел, в котором каждое последующее число получается умножением предыдущего на одно и то же число, называемое знаменателем прогрессии.

Формулы для n - го члена прогрессии

арифметической: а_п = а₁ + d(n — 1);

геометрической: а_п = a₁ q^{n - 1}.

Формулы для суммы п членов прогрессии арифметической:

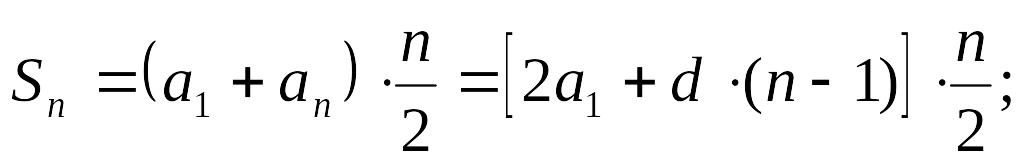
геометрической

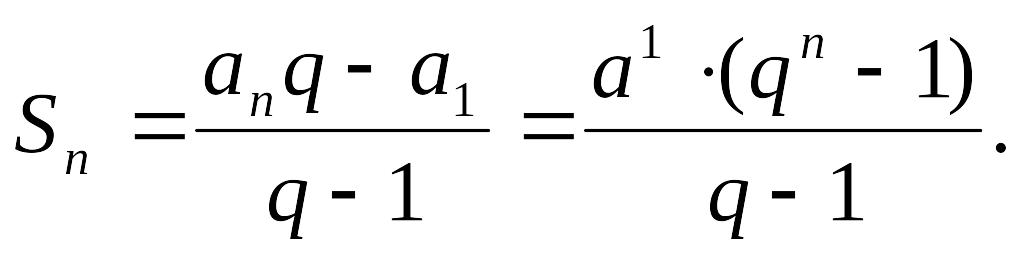
Если модуль знаменателя геометрической прогрессии менее единицы, |q| <0, то прогрессия называется убывающей. Если при этом число членов безгранично возрастает, то имеем:

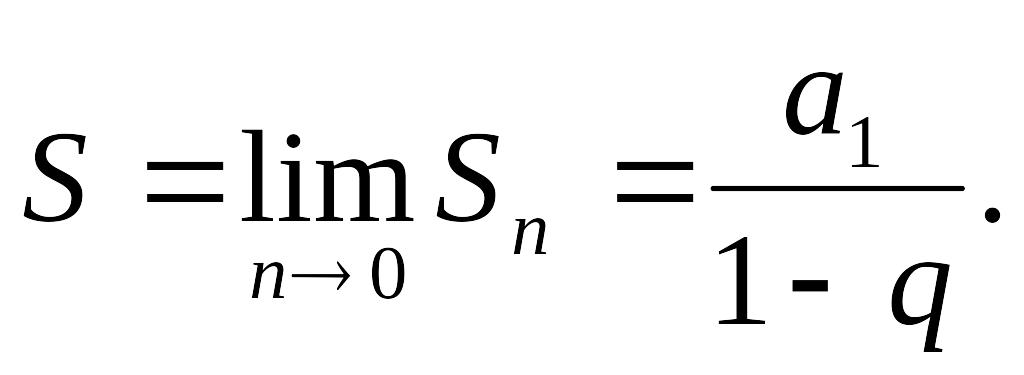
П.1.4 Факториал

Факториал натурального числа п обозначается и определяется равенством . Основное свойство факториала: . Понятие факториала распространяется на число 0, а именно: принимают 0!=1; при этом остается в силе основное свойство: . При больших п приближенные значения факториалов могут быть найдены с практически достаточной точностью по формуле Стирлинга:

.

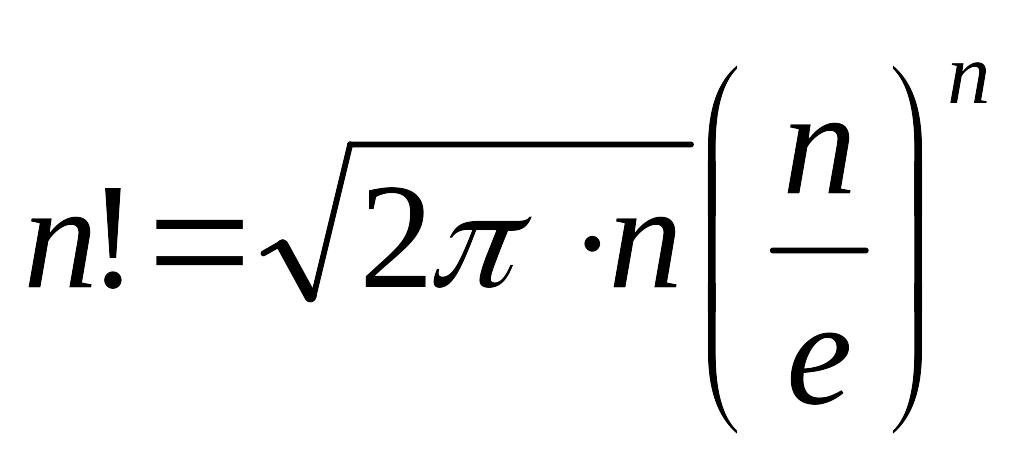П.1.5 Соединения

Группы элементов, отличающиеся одна от другой или порядком этих элементов, или самими элементами называются соединениями.

Если, например, из 10 различных цифр составлять группы по нескольку цифр в каждой, например такие: 123, 312, 8 056, 5 630, 42 и т. д., то будем получать различные соединения из этих цифр.

Размещениями из п элементов по т, называются соединения, из которых каждое содержит т элементов из заданных п и которые различаются или самими элементами, или их порядком. Число размещений из п элементов по т:

.

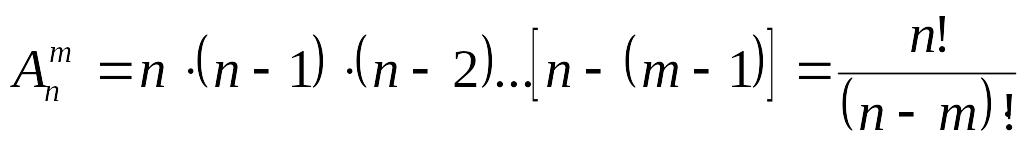Перестановками из п элементов называются соединения, из которых каждое содержит все п элементов и которые различаются только порядком элементов. Число перестановок из п элементов:

Сочетаниями из п элементов по m, , называются соединения, из которых каждое содержит m элементов из заданных п и которые различаются, по крайней мере, одним элементом. Число сочетаний из п элементов по m:

Свойство сочетаний:

.

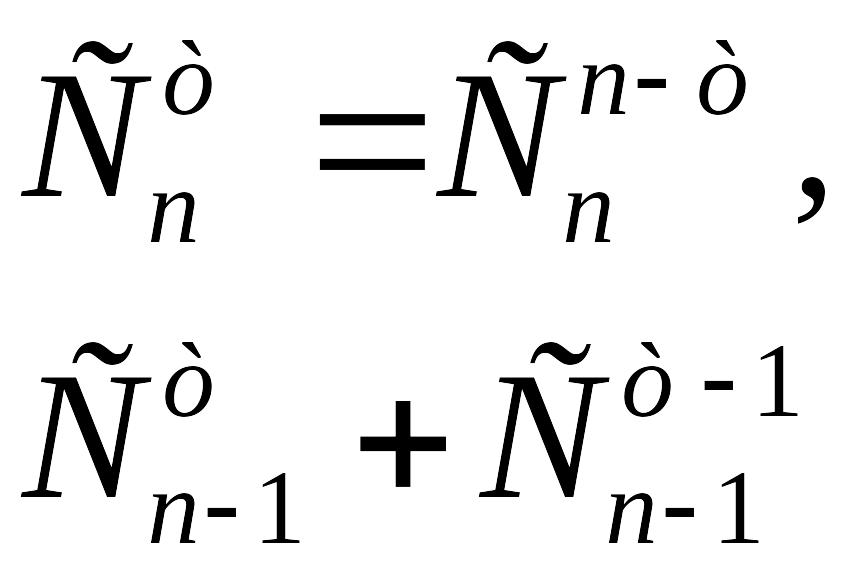Число сочетаний обозначается также знаком .