1.1.4 Координаты вектора
Три
взаимно перпендикулярные
оси
X,
Y,
Z
(рис.1.9)
образуют декартову прямоугольную
систему координат. Имеется
две системы прямоугольных координат —
правая и левая.
Для правой системы координат поворот оси X на 900 до совмещения ее с осью Y виден со стороны оси Z против часовой стрелки, а для левой — по часовой.
Прямоугольными координатами вектора называются проекции вектора на оси координат (рис. 1.9). Координаты вектора обозначаются буквами ax ,ay, az.
Запись:
.
(1.3)
Векторы
изображенные на рисунке, называются
единичными
ортами
(единичными векторами) координатных
осей. Их модули равны единице, а направления
совпадают с направлением осей OX,
OY
и OZ.
Зная проекции вектора
,
можно представить его как
(1.4)
1.1.5 Длина вектора
Длина вектора = {сx ,сy, сz} выражается через его координаты по теореме Пифагора формулой
.
(1.5)
После определения , являющегося суммой векторов и , часто возникает задача нахождения модуля вектора , т. е. его длины. Возможны следующие случаи:
1. Складываемые
векторы сонаправлены
(
).
В этом случае от векторной записи
(1.6)
легко перейти к скалярной, спроектировав уравнение (1.6) на ось OX (рис.1.10), параллельной векторам
OX:
. (1.7)
2. Складываемые
векторы 
противоположно
направлены
.
Спроектировав уравнение
на ось OX (рис. 1.11), получаем
OX:
. (1.8)
3. Складываемые
векторы перпендикулярны
(рис. 1.12). Модуль вектора
находим по теореме Пифагора, записанной
для прямоугольного треугольника ODE.
и
- катеты треугольника,
-
его гипотенуза. Поэтому
. (1.9)
4. Угол 
между
складываемыми
векторами произвольный
(рис. 1.13) (α
не равен 0°, 90°, 180°, как это имело место
выше). В этом случае применяется теорема
косинусов: Квадрат одной стороны
треугольника равен сумме квадратов
двух других сторон минус удвоенное
произведение сторон на косинус угла
между ними. Для треугольника ODE,
в котором известны стороны,
и
а также угол
α , теорема
запишется как
(1.10)
Применяя теорему
косинусов, следует помнить, что в ней
идет речь не об угле между складываемыми
векторами
и
(угле β), а об угле
α = 180° - β. Так как cos (180° - β ) = -cosβ , выражение (1.10) можно записать в следующем виде:
.
(1.10а)
1.1.6 Углы между осями координат и вектором
Углы α,β,γ образуемые
положительными направлениями OX,
OY,
OZ
с вектором
=
{ax
ay
az}
(рис. 1.14), можно
найти по формулам
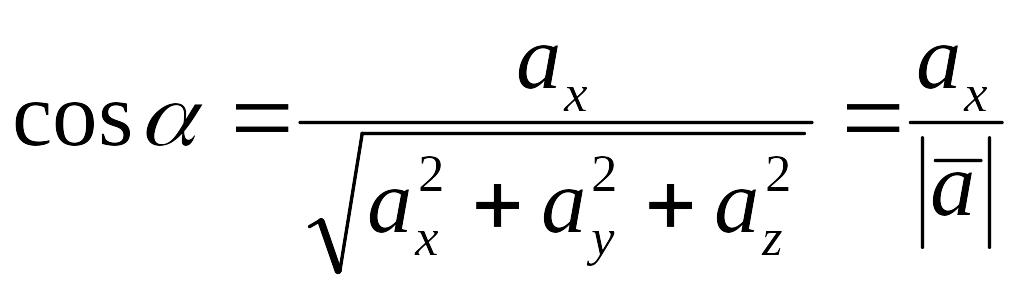, (1.11)
,
(1.12)
Рис. 1.14
.
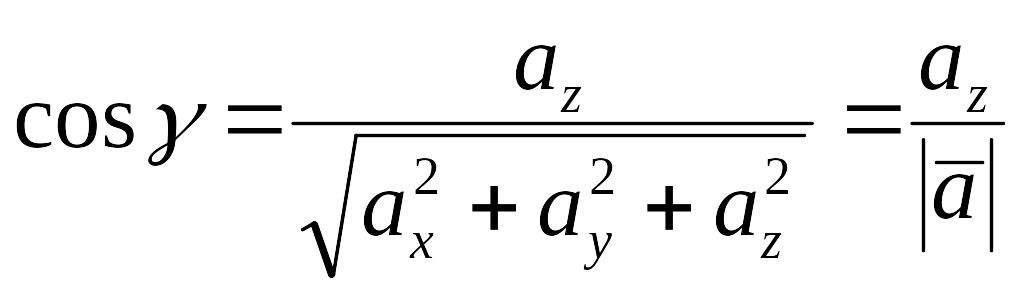Примеры решения задач
Задача 1.1
Самолет держит
курс на север со скоростью
=
200м/с относительно Земли. Дует западный
ветер со скоростью относительно Земли
=
15 м/с. Найти скорость самолета v
относительно воздуха.
Д
ано:
=
200 м/с;
=
15 м/с.
Найти: v.
Решение
Скорость
самолета относительно воздуха 
равна
.
Изобразим треугольник скоростей (рис.
З 1.1).
Так как
,
модуль искомой скорости находим по
теореме Пифагора:
=200,56м/с.
Ответ: скорость самолета относительно воздуха
v = 200,56м/с.
Задача 1.2
К телу приложены
силы 
и 
,
угол между которыми 
= 20°. Найти модуль результирующей силы
,
действующей на тело, если
=
=
20Н.
Д
ано:
= 20°;
=
20 Н;
=
20Н.
Найти: F.
Решение.
Результирующая
сила
,
действующая на тело, — это векторная
сумма сил
и
:
(рис. З 1.2). Найдем сумму векторов
и
по
правилу параллелограмма. Для треугольника
сил ОДЕ
(ОД=
,
ДЕ=
,
ОЕ=
)
запишем теорему косинусов в виде:
,
где α =180° -
.
Так как по условию
то
39.4Н.
Ответ модуль
результирующей силы F
39,4
Н.
З
адача
1.3
Тело массой m=
1кг движется с постоянной по модулю
скоростью v
= 10м/с по окружности. Найти модуль
изменения импульса тела
при прохождении четверти окружности
(импульсом называется произведение
массы тела m
на его скорость 
).
Дано: v = 10 м/с; m = 1кг.
Найти: .
Решение. Изменение
какой-либо величины - это разность
конечной и начальной величины. Значит,
= 
- 
.
Пусть тело находилось в точке 1 и, двигаясь
по часовой стрелке, оказалось в точке
2. Так как импульс по определению есть
= m
,
то векторы
и
сонаправлены. Вектор скорости
,
направлен по касательной к траектории
тела. Поэтому в точке 1 вектор
,
горизонтален, а в точке 2 вектор
вертикален. Построим разность векторов
и
(рис.
З 1.2). Тик как
,
то по теореме Пифагора
кг*м/с
.
О
кг*м/с
.
Задача 1.4
Вектор скорости
тела меняется со временем по закону
,
м/с, где t
- время, а
,
,
— орты координатных осей. Найти
зависимость модуля скорости от времени
v
(t).
Дано: , м/с.
Найти: v(t).
Решение. В
данной задаче вектор
выражен через проекции на координатные
оси и орты
,
,
координатных
осей (см. с. 16). Сомножители при ортах
,
,
- это проекции
вектора скорости на оси OX,
OY,
OZ,
соответственно. Таким образом,
= 6t
м/с, 
=
4м/с,
= -12
м/с. Тогда модуль вектора скорости
,м/с.
Ответ: зависимость
модуля скорости от времени
,м/с.
Задача 1.5
Найти угол α между
силой
,
Н, действующей на тело, и осью ОХ
в момент
времени t
= 1с.
Дано:
,H;
t
= 1 с.
Найти:α.
Решение. Найдем
длину вектора
.
Как и в
предыдущей задаче, запишем компоненты
вектора
:
Fx= 4 Н, Fy =7t Н, FZ= 2t Н.
Используя формулу (1.11), получаем
.
В данную формулу подставим значение времени t = 1 с:
,
.
Ответ: между силой
и осью ОX
угол
.