2.11 Другие формы условий равновесия плоской системы

Условия равновесия произвольной плоской системы сил, записанные в виде (2.48) и (2.49), назовем основной формой уравнений равновесия. В инженерной практике часто целесообразно использовать другие формы условий равновесия рассматриваемой системы сил. Получим эти условия.

Т еорема 1. Для равновесия плоской системы сил необходимо и достаточно, чтобы алгебраические суммы моментов сил системы относительно любых трех точек плоскости, не принадлежащих одной прямой, обращались в нуль.

Мы должны доказать, что при

;

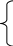
; (2.60)

.

система находится в равновесии.

Пусть А, В и С — произвольные точки, определяющие плоскость действия сил . Если система находится в равновесии, то должны выполняться условия (2.48) и (2.49). Последнее уравнение условий (2.49) означает, что алгебраическая сумма моментов сил относительно любой точки, в том числе точек А, В и С, равна нулю, что доказывает необходимость условия (2.60). Достаточность вытекает из того, что если бы при одновременном их выполнении система сил не находилась в равновесии, то она приводилась бы к равнодействующей, одновременно проходящей через точки А, В и С. Но это невозможно, потому что три точки не лежат на одной прямой.

В дальнейшем точки, относительно которых составляются условия (2.60), будем называть моментными.

Т еорема 2. Для равновесия плоской системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы алгебраические суммы, их моментов относительно любых двух точек в плоскости действия сил были равны нулю и сумма проекций этих сил на ось, не перпендикулярную прямой, соединяющей моментные точки, также обращалась в нуль, т. е.

;

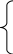
; (2.61)

.

причем ось ОX не перпендикулярна АВ.

Необходимость равенств (2.61) вытекает непосредственно из основной формы уравнений равновесия (2.49). Как и в доказательстве теоремы 1, из первых двух равенств (2.60) следует, что если система имеет равнодействующую , то линия ее действия проходит через точки А и В (рис. 2.35) и проекция на ось X, не перпендикулярную АВ, будет отлична от нуля. Но это означает, что не выполняется третье из условий (2.61). Следовательно, равнодействующая должна быть равна нулю и система находится в равновесии.

С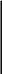 ледствие. Для равновесия плоской системы параллельных сил необходимо и достаточно обращение в нуль алгебраических сумм моментов всех сил относительно любых двух точек, для которых отрезок АВ не параллелен силам, т. е.

;

.

и АВ не параллельно .

Справедливость утверждения вытекает из условий (11.2), поскольку последнее равенство этих условий для случая параллельных сил удовлетворяется тождественно.

Заметим следующее. При использовании условий равновесия в форме (2.60) - (2.61) за моментные точки удобно брать те, через которые проходят искомые силы, например, реакции связей. Такой выбор моментных точек существенно упрощает процедуру определения неизвестных сил.

Рассмотрим, например, брус АВ, один конец которого заделан в стену (рис. 2.36а). На брус действует плоская система сил . При освобождении бруса от заделки мы должны приложить к части А'А распределенные силы. Если эти силы привести к точке А, то получим силу - главный вектор сил, распределенных по длине А'А, а также пару с моментом - главный момент распределенных сил относительно точки А. Выполняя разложение силы на составляющие по осям X, Y, мы получаем систему реактивных усилий Х_А, Y_A, M_A, показанную на рис. (2.36б). Выбирая теперь А в качестве моментной точки, можно записать: _,

откуда сразу же определяется реактивный момент М_А.