2.10 Плоская система сил. Теорема Вариньона

Большинство практических задач техники приводят именно к этому случаю воздействия сил на твердое тело. Поэтому рассмотрим его особо.

Пусть к твердому телу приложена неуравновешенная система сил , расположенная в одной плоскости. Выберем в этой плоскости произвольную точку О и приведем заданную систему сил к центру О. При этом возможны три случая.

1. Если при приведении плоской системы сил к какому–либо центру окажется, что главный вектор отличен от нуля, а главный момент обращается в нуль, то такая плоская система сил приводится к равнодействующей, величина и направление которой совпадает с главным вектором 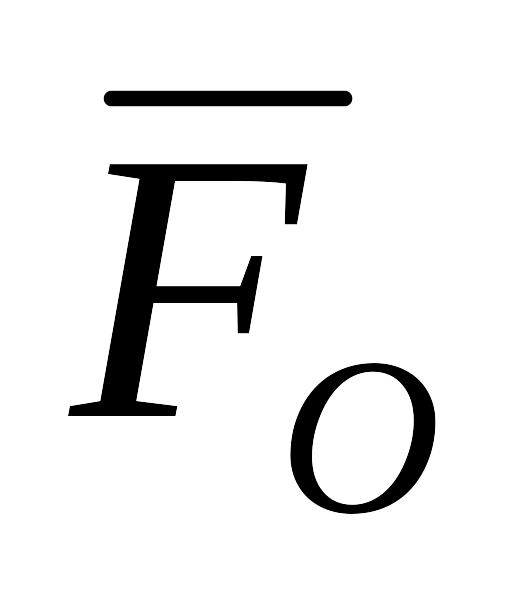системы .

2. Второй возможный случай имеет место тогда, когда в результате приведения плоской системы сил к некоторому центу О главный вектор по определению , а главный момент . Поскольку главный вектор по определению равен векторной сумме сил системы, то при он обращается в нуль независимо от выбора центра приведения. Отсюда вытекает, что в рассматриваемом случае главный момент также не зависит от центра приведения.

3 . Пусть после приведения плоской системы сил к некоторому центру О оказалось, что главный вектор и главный момент одновременно отличны от нуля ( , ). Такую систему сил можно упростить и привести к одной равнодействующей силе .

В самом деле, пусть мы привели систему к центру О (рис. 2.33). Как показано в §7, пару сил в плоскости ее действия можно поворачивать, передвигать в любую току плоскости и изменять плечо и силы пары, сохраняя постоянным алгебраическое значение ее момента. Выберем силы ( , ), входящие в пару с моментом , параллельными главному вектору , и потребуем, чтобы модули этих трех сил были равными: . Тогда плечо d (рис. 2.33) пары ( , ) определим по формуле

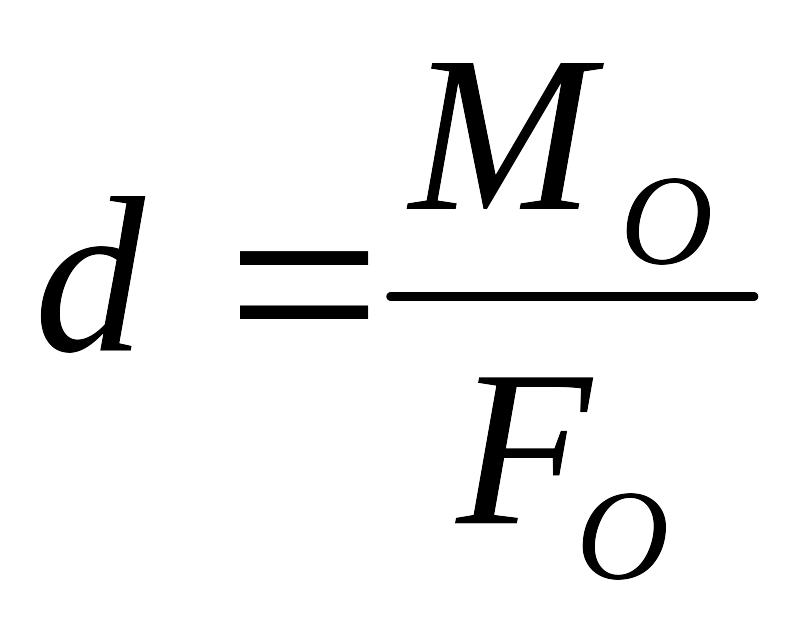. (2.54)

Система сил ( , ) эквивалентна нулю, и ее можно отбросить. Таким образом, остается одна сила , приложенная к телу в точке О₁ на расстоянии d от центра приведения О. Равнодействующую можно перенести в любую точку линии ее действия. Для случая, когда система сил, приложенных к твердому телу, приводится к равнодействующей, часто оказывается полезным следующее.

Т еорема Вариньона. Если система сил, приложенных к твердому телу, приводится к равнодействующей, то момент этой равнодействующей относительно какой-либо точки равен сумме моментов всех сил системы относительно той же точки.

П редположим, что на тело действует система сил (необязательно плоская) . По условию теоремы система приводится к равнодействующей, которую обозначим через . Добавим уравновешивающую силу , равную по модулю равнодействующей и противоположно ей направленную вдоль общей линии действия (рис. 2.34). Полученная после добавления система сил должна удовлетворять условиям равновесия (2.54). Согласно второму из этих условий, сумма моментов сил новой системы относительно любой точки О должна обращаться в нуль:

. (2.55)

Так как и - две равные и противоположно направленные силы с общей линией действия, их моменты относительно точки О различаются только знаками, т. е.

. (2.56)

Подстановка (2.56) в уравнение равновесия (2.55) дает:

. (2.57)

и теорема доказана.

Проведем через точку О произвольную ось Z и спроектируем векторное равенство (2.57) на ось Z, используя теорему 2 из 2.6. Получим:

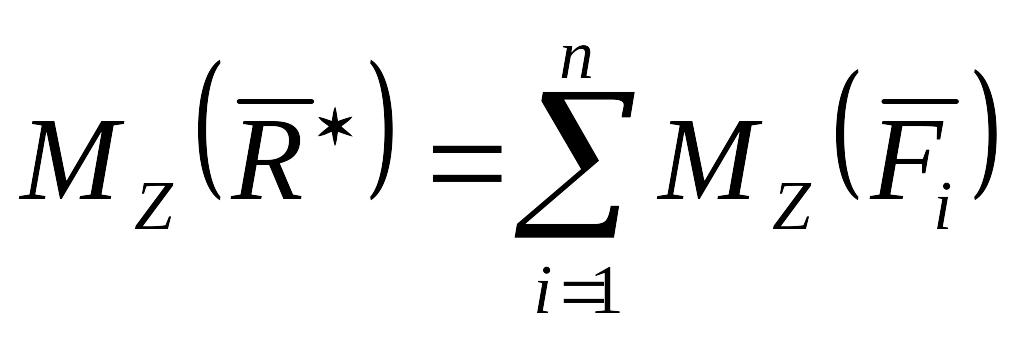, (2.58)

т. е. момент равнодействующей относительно произвольной оси равен сумме моментов сил системы относительно той же оси.

Если система сил плоская, а ось Z перпендикулярна плоскости действия сил, то из равенства (2.58) получаем:

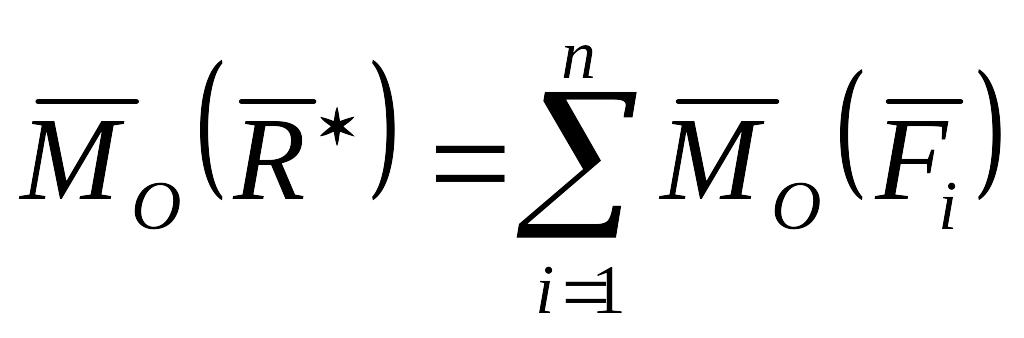. (2.59)

Этот результат известен как теорема Вариньона для плоской системы сил: алгебраическая сумма моментов всех сил плоской системы относительно любой точки равна моменту равнодействующей этой системы относительно той же точки.