2.5 Аналитический способ определения равнодействующей системы сходящихся сил. Условия равновесия

Каждую силу системы сходящихся сил можно разложить на составляющие по осям прямоугольной декартовой системы координат:

, (2.7)

где - орты осей X, Y, Z.

Разложив каждую силу в формуле (2.7) и вынося орты за знаки сумм, получим:

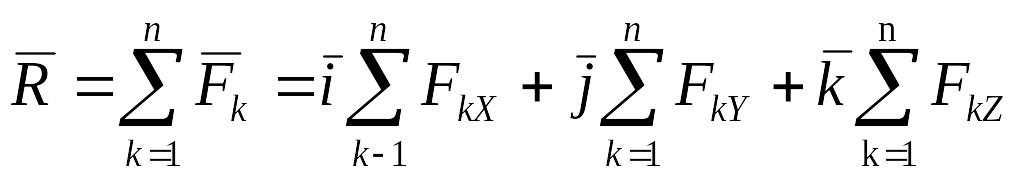(2.8)

Аналогично можно разложить и равнодействующую:

. (2.9)

Приравнивая выражения (2.9) и (2.8), получим, что

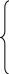
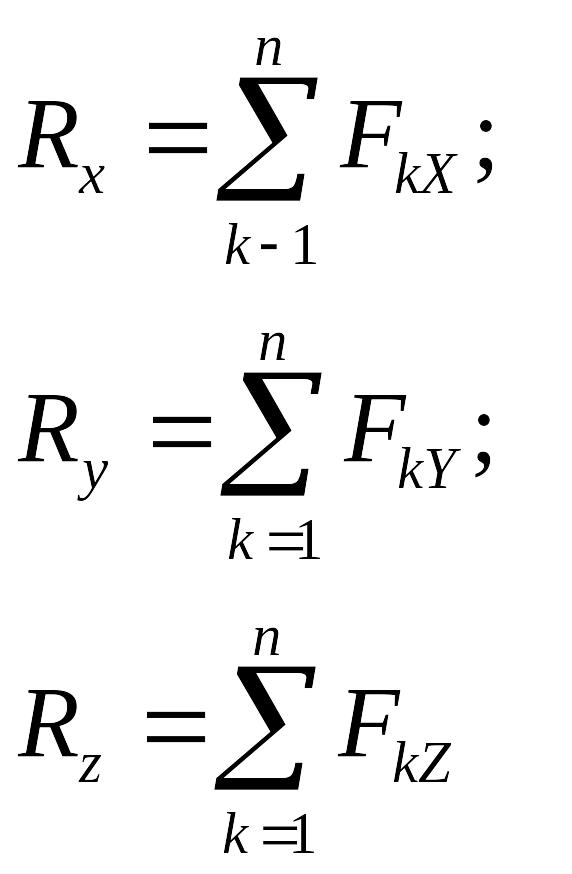. (2.10)

Определив проекции равнодействующей, можно найти ее модуль

, (2.11)

а также косинусы углов между вектором силы и осями координат:

. (2.12)

Эти косинусы связаны между собой соотношением

.

Косинусы углов между некоторым вектором и осями координат называют также направляющими косинусами данного вектора.

Для системы взаимно уравновешенных сил , а значит, , отсюда

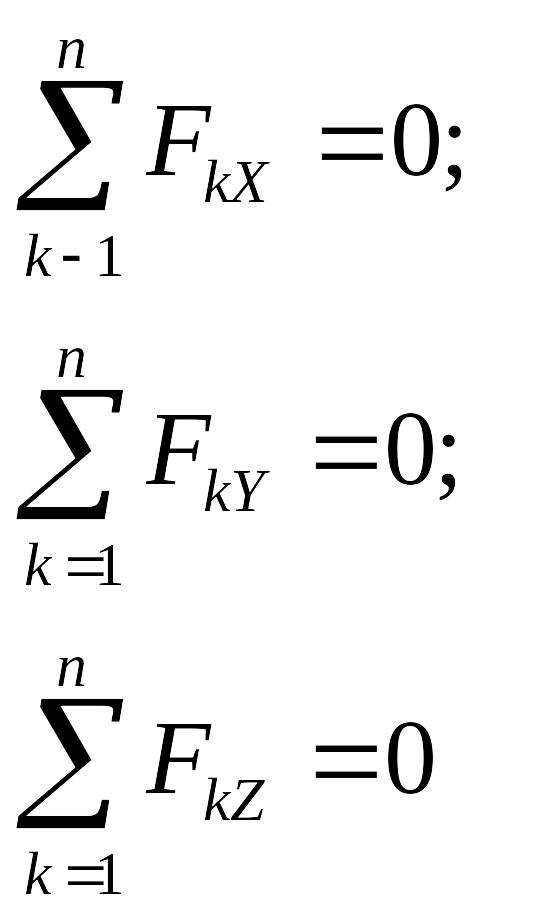
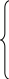. (2.13)

Уравнения (2.13) называют уравнениями (или условиями) равновесия системы сходящихся сил в аналитической форме. Для плоской системы сходящихся сил достаточно системы координат из двух осей, например X и Y. Условия равновесия имеют вид

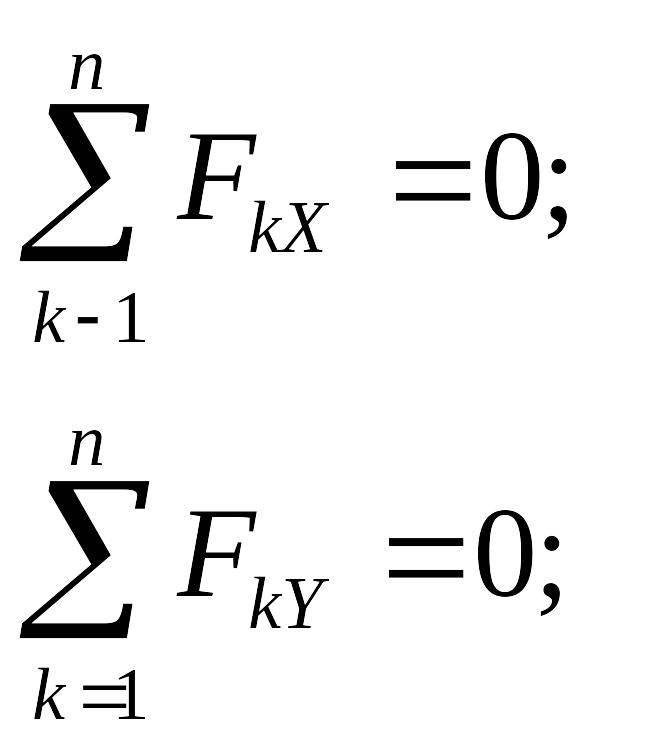
, (2.14)

и число неизвестных сил должно быть не более двух.

Задача 2.3

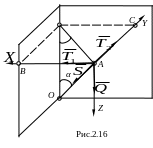
Груз Q, сила тяжести которого 120Н, поддерживается в равновесии стержнем АО и цепями АВ и АС (рис. 2.16). По концам стержня имеются шарниры. Длины цепей равны, т. е. АВ=АС; угол a = 300. угол ВАС- 90⁰. Определить силы в цепях АВ и АС и стержне АО, считая их невесомыми.

Решение. Рассмотрим равновесие узла А, заменив действие стержня и цепей на узел А реакциями , и , направив их, как показано на рис. 2.16. Получим систему четырех сил, сходящихся в точке А, направим оси координат вдоль цепей и нити подвеса груза. Составим уравнения равновесия, спроецировав систему сил на оси координат. При определении проекции реакции на оси X и Y применим метод двойного проецирования, спроецировав ее вначале на плоскость АXY, а затем на оси X и Y.

Имеем: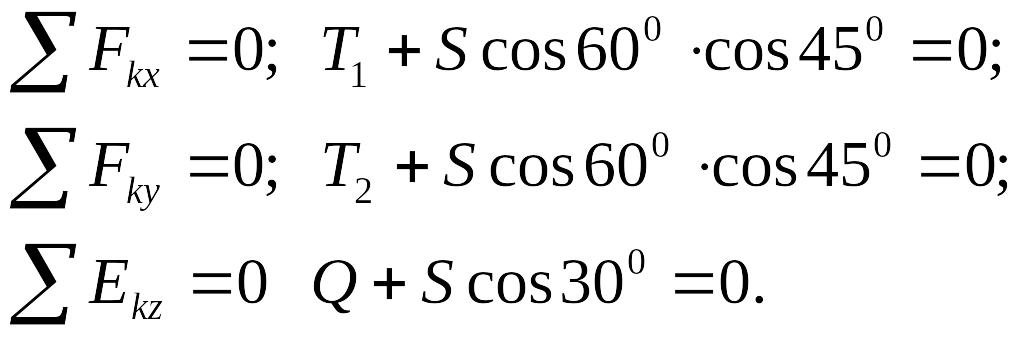

Из третьего уравнения находим, что S = -Q/cos30°= - 80 H.

Знак «минус» указывает на то, что выбранное направление реакции следует заменить на обратное.

Из первого и второго уравнений находим

.

Положительный знак результата свидетельствует о том, что выбранное направление реакций и соответствует действительному. На стержень АО и цепи действуют усилия, обратные реакциям. Следовательно, стержень АО сжат, а цепи растянуты (рис. 2.16).

2.6 Моменты силы относительно центра

и оси

Для рассмотрения различных систем сил необходимо ввести понятия алгебраического и векторного моментов силы относительно центра и момента относительно оси. Рассмотрим действия этих силовых факторов на твердое тело и их свойства.

М омент силы относительно центра. При рассмотрении плоской системы сил, приложенных к твердому телу, используется понятие алгебраического момента силы, относительно центра О. Под которым понимают, произведение силы на длину перпендикуляра, опущенного из центра на линию действия силы (рис. 2.17):

(2.15)

Алгебраический момент силы относительно центра О характеризует вращательный эффект силы относительно этого центра. Знак «плюс» берут в случае, когда сила стремится вращать тело против часовой стрелки, а «минус» - по часовой. Перпендикуляр h называют плечом действия силы относительно центра О. Согласно выражению (2.15) размерность момента силы - Н • м. Модуль момента силы равен удвоенной площади треугольника ОАВ:

, (2.15а)

и не меняется при переносе силы вдоль линии ее действия, так как при этом сохраняются основание треугольника АВ и его высота h.

Плоскость, определяемая треугольником ОАВ, - это плоскость действия момента силы.

В механике момент силы относительно центра принято изображать в виде вектора - называемого вектором момента силы относительно

ц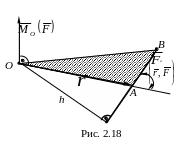 ентра. Этот вектор (рис. 2.18) направлен перпендикулярно к плоскости АОВ в ту сторону, откуда видно стремление силы повернуть плоскость АОВ, связанную с телом, против часовой стрелки. Проведем из центра О в начало вектора силы радиус-вектор и рассмотрим векторное произведение . По модулю

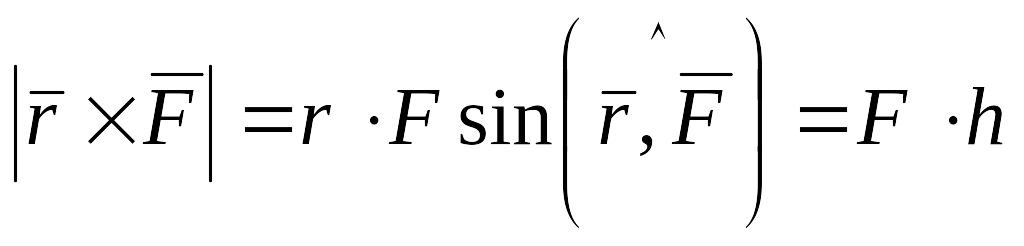, что совпадает с модулем момента силы (2.15). Направление вектора совпадает с направлением вектора момента силы . Отсюда вытекает, что вектор момента силы совпадает с векторным произведением :

. (2.16)

Пусть радиус-вектор и сила заданы своими проекциями на оси: и . Тогда выражение (2.16) можно записать как:

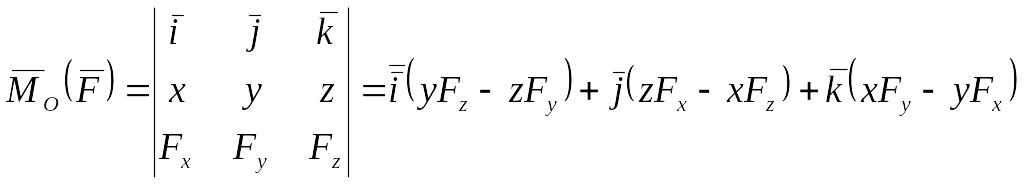(2.17)

С другой стороны, вектор можно спроецировать на оси координат:

(2.18)

Сопоставляя выражения (6.3) и (6.4), получим, что проекции вектора момента силы на оси координат можно вычислить по формулам:

. (2.19)

Для наглядности посмотрим, например, на систему координат со стороны оси Z (рис. 2.19). Ось Z направлена к читателю, - проекция силы на плоскость ОXY. Видно, что . Аналогично можно рассмотреть и . Исходя из разложения вектора момента силы в соответствии с выражением (2.18), по формулам векторной алгебры можно подсчитать его модуль:

,

или

, (2.20)

а также направляющие косинусы:

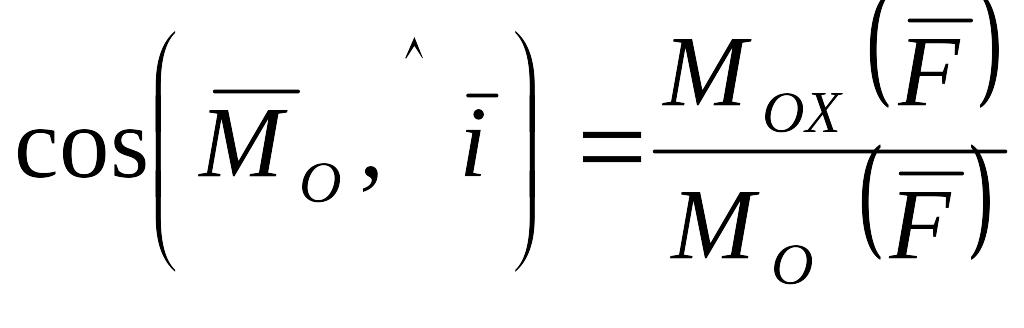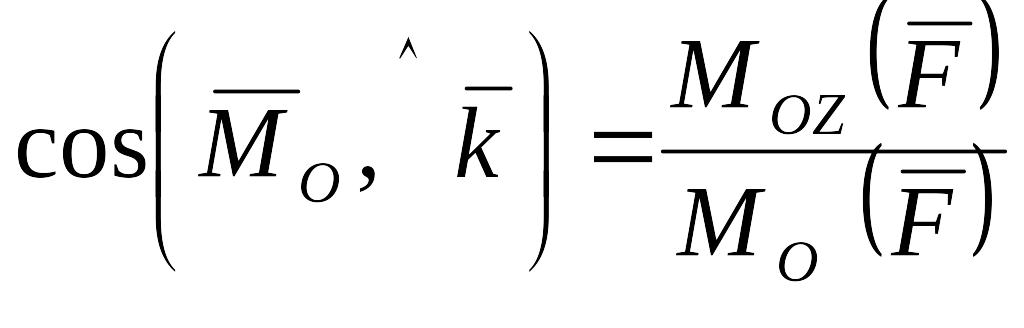; ; . (2.21)

М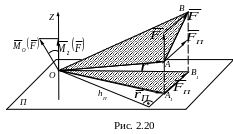 омент силы относительно оси. Алгебраическим моментом силы относительно оси Z называют алгебраический момент проекции F_n этой силы на плоскость П (рис. 2.20), перпендикулярную к оси Z, относительно точки О пересечения оси Z с плоскостью П:

(2.22)

Действительно, разложим силу на составляющие перпендикулярную оси Z, и , параллельную оси z (и, следовательно, перпендикулярную к плоскости П). Очевидно, что составляющая не стремится повернуть тело вокруг оси Z. Это может осуществить только составляющая .

Момент силы относительно оси равен нулю, если сила и ось Z лежат в одной плоскости. При этом сила либо пересекает ось и h = 0, либо параллельна ей.

Векторный момент силы (вектор момента силы) относительно оси направлен по оси в сторону, откуда действие момента видно против хода часовой стрелки. Его векторное выражение

(2.23)

Ранее было показано, что вектор момента силы относительно точки О перпендикулярен к плоскости треугольника ОАВ и по модулю равен удвоенной площади этого треугольника. Вектор момента перпендикулярен к плоскости треугольника ОА₁В₁ и также равен удвоенной его площади согласно выражению (6.1а). Но треугольник ОА₁В₁ — проекция треугольника ОАВ на плоскость П.

Следовательно, между площадями этих треугольников имеется следующая зависимость:

где γ - угол между плоскостями треугольников.

Угол γ равен также углу между перпендикулярами к плоскостям треугольников, а значит, и между векторами и . Таким образом, между этими векторами имеет место зависимость

, (2.24)

т. е. проекция вектора момента силы относительно некоторой точки О на ось, проходящую через эту точку, равна моменту силы относительно этой оси. Точка О на оси Z взята произвольно, и при любом ее положении проекция треугольника ОАВ на плоскость П равна треугольнику ОА₁В₁. Очевидно, что для силы, расположенной в плоскости П, угол γ = 0 и . При замене оси Z на оси X и Y, также проходящие через точку О, все приведенные ранее рассуждения остаются справедливыми. Отсюда следует, что на основании формул (2.19) и (2.24) имеют место соотношения:

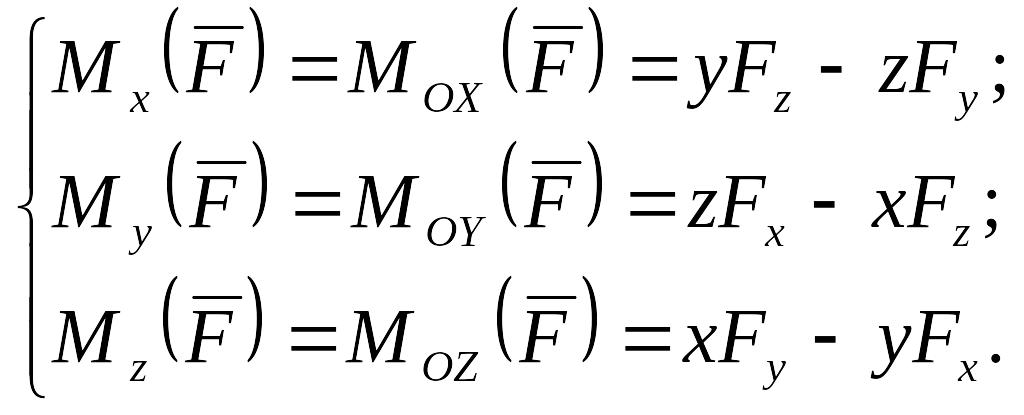(2.25)

т. е. проекции момента силы относительно центра О на оси декартовой прямоугольной системы координат равны моментам силы относительно координатных осей.

Г лавный момент системы сил относительно центра и оси. Пусть на тело действует система сил , ,… . Выберем некоторый центр О и покажем момент каждой силы относительно него в виде вектора . Получим систему векторов (где k = 1,2,..., п), приложенных к точке О (рис. 2.21). Эту систему векторов можно сложить по правилу параллелограмма или многоугольника и получить результирующий вектор , который называют главным моментом системы сил относительно центра О

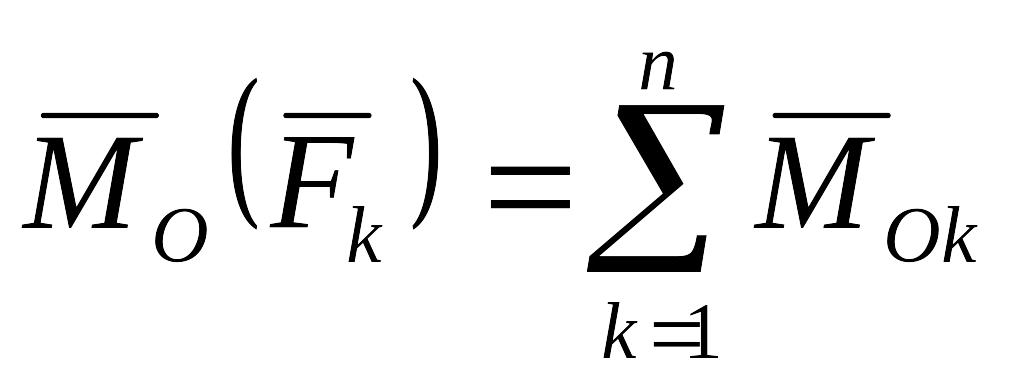. (2.26)

Главный момент выражается через проекции точек приложения сил x_k, y_k, z_k и проекции сил на оси координат F_kx., F_ky, F_kz следующим образом:

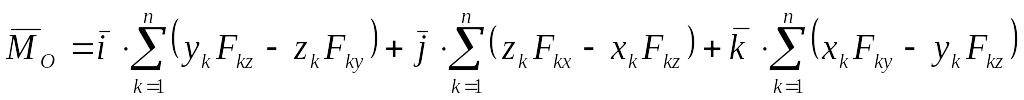(2.27)

Главный момент как вектор может быть спроецирован на какую-либо ось, например Z. При этом, как для любой результирующей, проекция ее на ось равна алгебраической сумме проекций составляющих на ту же ось:

.

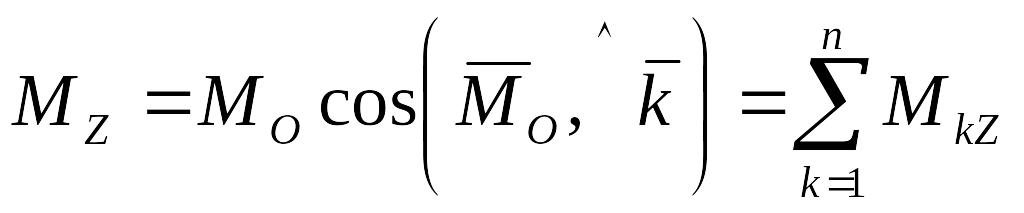Если силы лежат в одной плоскости, то векторы моментов этих сил перпендикулярны к этой плоскости и главный момент сил относительно некоторого центра О, расположенного также на плоскости, равен алгебраической сумме моментов сил относительно этого центра:

.

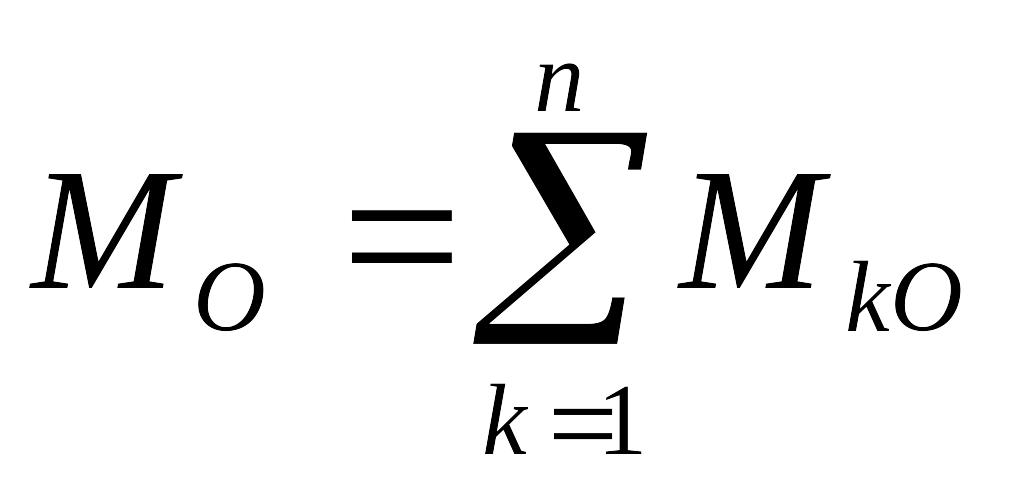Следовательно, тело находится в равновесии (не вращается относительно данного центра), если главный момент сил относительно этого центра равен нулю:

(2.28)

Это векторное условие равновесия тела, стремящегося повернуться вокруг центра О (т. е. в центре О тела имеется сферический шарнир).

Исходя из векторного условия и выражения (2.27), получим скалярные условия равновесия тела:

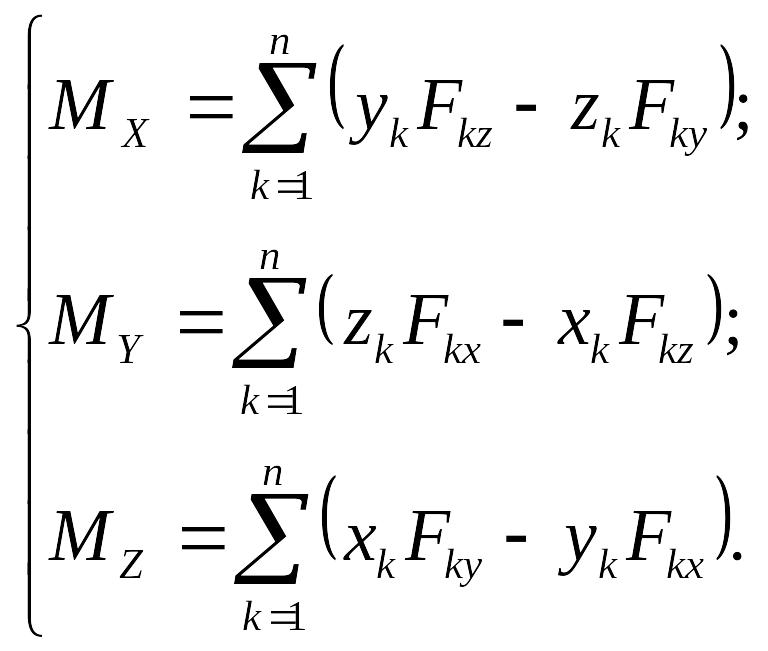(2.29)

Следовательно, тело находится в равновесии, если суммы моментов сил относительно координатных осей равны нулю.

Для равновесия тела относительно какой-либо одной оси необходимо, чтобы сумма моментов сил относительно этой оси равнялась нулю, например,

.

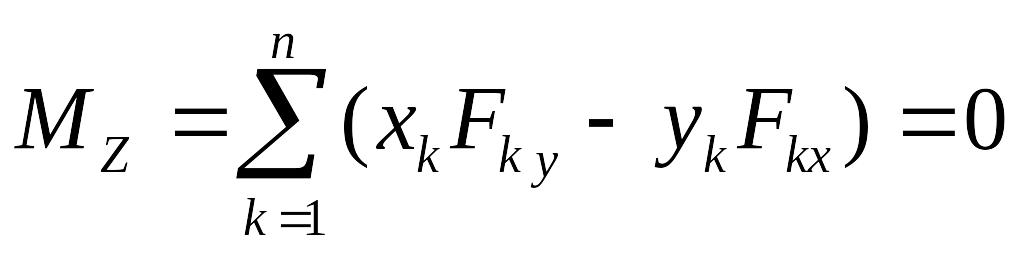Задача 2.4

Водонапорная башня, свободно стоящая на поверхности, подвержена ветровой нагрузке, результирующая которой приложена на высоте h (рис. 2.22). Сила тяжести башни . Определить значение силы , при котором башня опрокинется.

Решение. С ила стремится опрокинуть башню, повернув ее вокруг точки В. Составим сумму моментов сил относительно этой точки:

,

откуда

.

По условиям рассмотренного примера момент

М_опр = Fh называют опрокидывающим,

а момент

М_уд = GL/2 — удерживающим.

Отношение удерживающего момента к опрокидывающему называют коэффициентом устойчивости:

k_уст = М_уд / М_опр.

Для устойчивого состояния объекта необходимо, чтобы выполнялось неравенство kуст > 1, и при проектировании незакрепленных объектов выбором значения k_уст обеспечивается определенный запас их устойчивости.