Планування експерименту при вивченні діаграм «склад - властивість». Симплекс – решітчасті плани шеффе
Мета роботи: навчитися будувати план експерименту за допомогою симплекс-решітчастих планів Шеффе, розробляти математичну модель на основі аналізу отриманих експериментальних даних.
Симплексом називається випуклий багатогранник в багатомірному просторі, число вершин якого перевищує розмір цього простору на одиницю.
Якщо в кожній вершині симплекса прийняти вміст одного з компонентів суміші за 1 (або 100%), то кожній точці такого симплекса відповідає суміш відповідного складу, і навпаки, любій комбінації відносного вмісту q компонентів відповідає визначена точка на симплексі. Вершини симплекса відповідають 100–відсотковому вмісту компонентів, ребра – подвійним системам, грані – потрійним і т.д. Симплекс-решітчасті плани зручно записувати у вигляді таблиці.
При плануванні експерименту для дослідження діаграм “склад-властивість” припускається, що дослідна властивість є безперервною функцією аргументу і може з достатньою точністю бути описана поліномом. Поверхні відгуку в багатокомпонентних системах мають складний вид і для адекватного їх опису необхідні поліноми високої степені. В зв’язку з цим Шеффе запропонував описувати властивості сумішей приведеними поліномами.
Так як, найбільш часто доводиться досліджувати трьохкомпонентні суміші запишемо можливі приведені поліноми різної степені n для цього випадку:
Для
оцінки коефіцієнтів приведених поліномів
запропоновано плани, які забезпечують
рівномірний розподіл експериментальних
точок на (q-1)–мірному
симплексі. Точками таких планів є вузли
–
симплексних решіток, де q
– число компонентів,
n
– степінь полінома.
Алгоритм розрахунку:
1. Розрахункові формули коефіцієнтів поліномів отримують підстановкою в поліном послідовно координат всіх точок плану, а замість відгуків – відповідні даним точкам експериментальні значення у:
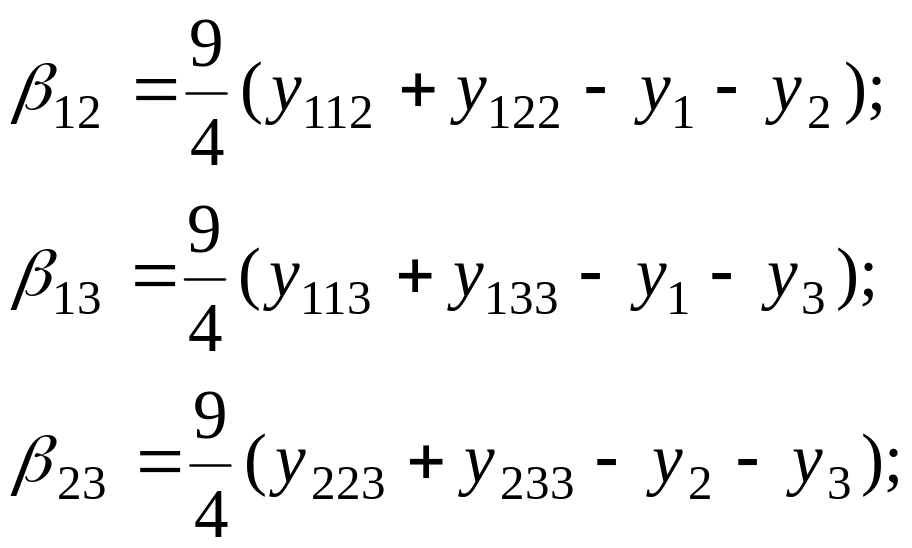
Для перевірки адекватності ставлять додаткові досліди в контрольних точках.
,
де уексп – експериментально знайдене значення вихідної величини в контрольній точці;
n – число паралельних спостережень в контрольній точці;
Sy – середньоквадратичне відхилення;
- параметр,
який залежить від порядку моделі і
координат контрольних точок на симплексі
(додаток 4).
Розрахункове
значення критерію Ст’юдента порівнюється
з табличним (tα/2l),
яке визначається при заданій рівні
значимості (α)
в залежності від числа контрольних
точок (l)
і числа ступенів свободи дисперсії
відтворення. Рівняння адекватне, якщо
Завдання: Для встановлення залежності в’язкості (у) трикомпонентних стекол від їх складу (хі) реалізовано симплекс – решітчастий план Шеффе {3, 2} (табл. 23). Результати паралельних спостережень надані в табл. 24.
Розрахувати коефіцієнти в поліномі другої степені та перевірити його адекватність.
У разу неадекватності математичної моделі контрольну точку внести в план експерименту та підвищити степінь поліному до неповної кубічної моделі.
Сформулювати висновок щодо розробленої математичної моделі.
Таблиця 23 – Симплекс – решітчастий план {3, 2}
-
Номер досліду
Відносний вміст компонентів
Х1
Х2
Х3
1
1,0
0,0
0,0
2
0,0
1,0
0,0
3
0,0
0,0
1,0
4
0,5
0,5
0,0
5
0,5
0,0
0,5
6
0,0
0,5
0,5
7 (контрольна точка)
0,333
0,333
0,333
Таблиця 24 – В´язкість стекол, Па·с
-
Варіант
Відгук
1
2
3
4
5
6
7
1
y1
5,1
10,1
7,1
10,1
8,1
14,0
10,1
y2
5,5
12,0
7,9
11,5
7,0
15,0
11,5
y3
5,6
11,8
9,1
12,0
9,2
13,4
11,0
2
y1
10,1
5,1
10,9
7,9
8,0
10,0
6,1
y2
8,5
5,5
11,5
8,8
9,9
11,0
6,5
y3
9,0
5,6
12,0
9,0
9,0
10,5
7,5
3
y1
6,1
5,0
9,1
13,0
5,0
11,1
9,5
y2
7,0
4,8
9,0
11,5
5,2
12,1
9,0
y3
7,1
5,6
8,7
12,1
6,1
11,5
9,8
4
y1
13,1
10,0
6,1
11,1
6,3
7,1
8,1
y2
12,9
9,5
6,6
10,3
7,0
8,1
8,8
y3
12,0
9,0
6,9
11,0
7,1
7,5
7,9
5
y1
5,1
10,1
13,1
6,1
8,2
7,1
10,5
y2
5,5
12,1
12,3
6,3
8,1
8,0
10,2
y3
6,2
11,5
12,5
7,0
8,9
7,5
10,8
6
y1
7,3
11,0
13,5
8,9
10,1
9,3
10,5
y2
7,0
12,0
13,0
9,1
10,6
9,3
11,3
y3
7,9
11,5
13,1
9,5
10,9
9,8
11,0
7
y1
8,1
10,3
11,9
9,0
12,1
9,5
11,2
y2
8,5
10,2
12,3
9,5
12,9
9,8
11,0
y3
8,6
11,0
12,5
9,1
12,5
9,9
10,5
8
y1
5,2
10,1
7,1
10,1
8,1
14,0
10,1
y2
5,5
12,0
7,9
11,5
7,0
15,0
11,5
y3
5,4
11,8
9,1
12,0
9,2
13,4
11,0
9
y1
10,1
5,4
10,9
7,9
8,0
10,0
6,1
y2
8,5
5,5
11,5
8,9
9,9
11,0
6,5
y3
9,0
5,8
12,0
9,1
9,0
10,7
7,5
10
y1
6,1
5,0
9,1
13,0
5,8
11,3
9,5
y2
7,0
4,8
9,0
11,5
5,2
12,1
9,6
y3
7,1
5,6
8,7
12,1
6,1
11,8
9,8
11
y1
13,3
10,8
6,1
11,1
6,3
7,1
8,1
y2
12,9
9,5
6,4
10,3
7,0
8,1
8,8
y3
12,0
9,0
6,9
11,2
7,5
7,5
7,9
12
y1
5,6
10,1
13,1
6,9
8,2
7,1
10,5
y2
5,5
12,4
12,3
6,3
8,0
8,1
10,2
y3
6,2
11,5
12,5
7,0
8,9
7,5
10,8
13
y1
7,8
13,0
13,5
8,9
10,1
9,3
10,5
y2
7,1
12,0
13,9
9,3
10,2
9,4
11,3
y3
7,9
11,5
13,1
9,5
10,9
9,8
11,0
14
y1
8,1
10,0
11,8
9,0
12,1
9,3
11,2
y2
8,5
10,2
12,3
9,2
11,9
9,8
11,0
y3
8,6
11,0
12,5
9,1
12,7
9,9
10,5
15
y1
5,1
10,1
7,6
10,1
8,1
14,0
10,1
y2
5,5
12,0
7,9
11,5
7,0
15,0
11,5
y3
5,6
11,8
8,1
13,3
8,2
13,4
11,0
16
y1
10,1
5,1
10,9
9,9
8,0
10,0
6,1
y2
8,5
5,5
11,5
8,8
9,9
11,0
6,5
y3
9,0
5,6
12,0
9,0
8,4
10,5
7,5
17
y1
6,1
5,0
9,1
13,0
5,0
11,1
9,5
y2
7,1
6,8
9,5
11,2
5,2
12,1
9,0
y3
7,1
5,6
8,7
12,1
6,1
11,5
9,8
18
y1
13,1
10,2
6,1
11,4
6,3
7,1
8,1
y2
12,9
9,5
6,6
10,3
7,0
8,1
8,8
y3
12,0
9,7
5,9
11,0
7,1
7,5
7,9
19
y1
5,1
10,1
13,1
6,1
8,2
7,1
10,5
y2
5,5
12,1
12,8
6,9
8,1
8,3
10,2
y3
6,2
11,1
12,5
7,0
8,9
7,5
10,8
20
y1
7,3
11,0
14,5
8,9
11,1
9,3
10,5
y2
7,0
12,0
14,0
9,1
11,6
9,3
11,3
y3
7,9
12,5
14,1
9,5
11,9
9,8
11,0
21
y1
8,8
10,9
11,7
9,0
12,1
9,5
11,2
y2
8,5
10,2
12,3
9,6
12,4
8,9
10,7
y3
8,6
11,0
12,5
9,1
12,5
9,9
10,5
22
y1
14,3
11,8
6,1
11,1
6,8
7,1
9,1
y2
13,9
10,5
6,3
12,3
7,9
8,1
8,8
y3
12,0
9,8
5,9
11,2
8,5
8,5
7,9
23
y1
6,6
12,1
12,1
7,9
8,3
7,1
9,5
y2
5,5
12,4
12,3
8,3
7,0
7,1
10,2
y3
6,0
11,5
11,5
7,0
8,9
7,5
11,8
24
y1
7,3
13,3
12,5
8,9
11,1
10,3
10,5
y2
8,1
12,7
11,9
10,3
10,2
9,7
12,3
y3
7,9
11,5
13,1
9,5
9,9
9,8
12,0
25
y1
8,2
10,1
11,4
9,6
11,1
8,3
10,2
y2
8,5
10,2
12,0
9,2
11,0
8,8
11,0
y3
8,7
11,6
12,5
7,1
12,7
9,9
12,5
26
y1
6,1
11,1
7,7
10,2
8,3
14,2
10,1
y2
5,5
12,0
7,9
11,5
7,0
15,3
13,5
y3
5,6
11,8
8,3
12,3
8,0
13,4
11,0
27
y1
11,1
5,2
9,9
9,9
8,4
10,1
5,1
y2
9,5
6,5
11,5
7,8
9,3
11,6
8,5
y3
9,0
7,6
12,3
9,0
7,4
10,5
10,5
28
y1
5,7
5,0
10,1
12,0
5,0
11,7
9,6
y2
7,8
5,8
9,5
11,2
4,2
12,1
9,0
y3
7,1
5,6
8,7
13,7
6,1
11,5
9,8
29
y1
12,1
10,1
7,1
12,4
6,3
7,8
7,1
y2
12,9
9,8
6,4
10,8
5,0
9,1
8,0
y3
11,0
9,7
5,9
11,2
7,1
7,5
7,9
30
y1
5,1
10,1
13,1
6,3
8,2
9,1
12,5
y2
5,4
13,1
13,8
6,9
9,1
8,3
10,2
y3
6,4
11,1
12,5
7,4
8,9
9,5
13,4