
Государственный комитет Российской федерации
по высшему образованию
Саратовский государственный технический университет
ОПРЕДЕЛЕНИЕ СКОРОСТИ СКАТЫВАНИЯ ШАРА
МЕТОДОМ БАЛЛИСТИЧЕСКОГО МАЯТНИКА.
Методические указания
к учебно-исследовательской
лабораторной работе
по курсу общей физики
Одобрено
Редакционно-издательским советом
Саратовского Государственного
технического университета
Саратов, 2000 г.
ПОСТАНОВКА ЦЕЛИ РАБОТЫ
Рис.1
Это вариант довольно стандартной инженерной задачи при проектировании различных систем, например, подающих транспортеров, желобов и т.п. Такую задачу можно решить аналитически, если известна форма скатывающего тела и другие необходимые параметры, а можно - экспериментально, если часть параметров задана неточно или просто неизвестна. Предлагаемая здесь задача может быть решена и аналитически и в эксперименте. При некоторых упрощающих предположениях мы продемонстрируем один из приемов аналитического решения и получим искомое значение скорости в конце пути скатывания шара. После изучения этого приема. Вам предлагается измерить значение скорости в эксперименте, используя один из классических способов - метод баллистического маятника. Сравнивая полученные результаты, Вы, в отчете по работе, попробуйте оценить степень совпадения значений скорости и предложите возможные причины их различия.
Аналитическое решение задачи
Вычисление скорости шара в нижней точке желоба.
Рис. 2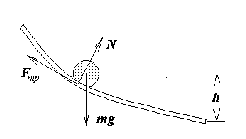
![]() (1)
(1)
Выделим три главных, действующих на шар силы: сила тяжести - mg, сила нормальной реакции опоры - N и сила трения - Fтр (см. Рис.2).
Работа силы тяжести
![]() может быть представлена, как разность
двух величин
может быть представлена, как разность
двух величин
![]() ,
каждая из которых называется потенциальной
энергией поля силы тяжести, поэтому A
,
каждая из которых называется потенциальной
энергией поля силы тяжести, поэтому A![]() =
Eпот1
= mgh, так как
Eпот2
=0. Работа
силы нормальной реакции AN
равна нулю, так как эта сила действует
перпендикулярно траектории. При
вычислении работы силы трения будем
предполагать, что при движении шара по
желобу не возникает скольжения. В этом
случае сила трения работы не производит
потому, что она приложена к тем точкам
шара, которые лежат на мгновенной оси
вращения, а мгновенная скорость таких
точек равно нулю, следовательно, данная
точка не перемещается и Aтр=0.
Роль силы трения в этом случае сводится
к тому, чтобы привести тело во вращение
и обеспечить чистое качение, представляющее
собой движение, при котором мгновенные
оси вращения не перемещаются, а
последовательно заменяются другими,
близлежащими осями - множествами точек
катящегося тела. Понятно, что такая
модель, при конечном значении коэффициента
трения, может работать не при любых
формах кривой скатывания. Однако, при
наличии проскальзывания описание сильно
усложнится и мы не будем приводить его
здесь.
=
Eпот1
= mgh, так как
Eпот2
=0. Работа
силы нормальной реакции AN
равна нулю, так как эта сила действует
перпендикулярно траектории. При
вычислении работы силы трения будем
предполагать, что при движении шара по
желобу не возникает скольжения. В этом
случае сила трения работы не производит
потому, что она приложена к тем точкам
шара, которые лежат на мгновенной оси
вращения, а мгновенная скорость таких
точек равно нулю, следовательно, данная
точка не перемещается и Aтр=0.
Роль силы трения в этом случае сводится
к тому, чтобы привести тело во вращение
и обеспечить чистое качение, представляющее
собой движение, при котором мгновенные
оси вращения не перемещаются, а
последовательно заменяются другими,
близлежащими осями - множествами точек
катящегося тела. Понятно, что такая
модель, при конечном значении коэффициента
трения, может работать не при любых
формах кривой скатывания. Однако, при
наличии проскальзывания описание сильно
усложнится и мы не будем приводить его
здесь.
Теперь соотношение (1) может быть переписано как
![]() . (2)
. (2)
Здесь кинетическая энергия представлена суммой всего двух слагаемых, первое из которых - кинетическая энергия поступательного движения шара, а второе - кинетическая энергия вращения шара вокруг своего центра. Выделенная последняя часть предыдущего предложения очень важна - ведь в действительности шар вращается вокруг мгновенной оси вращения, проходящей через точки касания шаром желоба. При записи этой, простой на первый взгляд, формулы использован мощный прием - теорема Кенига о кинетической энергии твердого тела (см. Приложение 1). Действительно, при столь сложном движении шара включающем поступательное и одновременно вращательное движение вокруг мгновенной оси, записать выражение для кинетической энергии непросто, поскольку кинетическая энергия системы складывается из кинетических энергий всех его материальных точек. Шар в данном случае нельзя представить материальной точкой и поэтому необходимо знать скорость каждой из его частиц, которые движутся каждая по своей траектории (попробуйте изобразить эти траектории и тогда сможете оценить красоту и важность теоремы Кенига).
Для нахождения связи между линейной V и угловой скоростью w вспомним, что скорость любой точки твердого тела Vi можно представить в виде суммы двух скоростей: Vс - скорости движения центра масс твердого тела и Ui - скорости этой точки относительно системы координат, связанной и движущейся вместе с центром масс:
![]() . (3)
. (3)
Применим соотношение (3) к точкам шара, катящегося со скоростью V, и касающимся в некоторый момент времени желоба (точкам мгновенного центра качения):
![]()
Величина r, называемая радиусом качения и являющаяся расстоянием между центром скатывающегося шара и мгновенной осью вращения, связана с радиусом шара R (см. Рис.3) соотношением:
![]() .
(4)
.
(4)
Рис. 3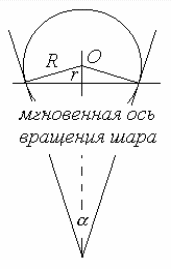
![]() (5)
(5)
Подставляя формулу (5) в соотношение (2) получим выражение для скорости шара в нижней точке желоба:
 (6)
(6)
Учитывая, что
главный момент инерции шара (при вращении
вокруг собственной оси) равен
![]() [2,
4], то
после подстановки
(4) в (6) получим:
[2,
4], то
после подстановки
(4) в (6) получим:
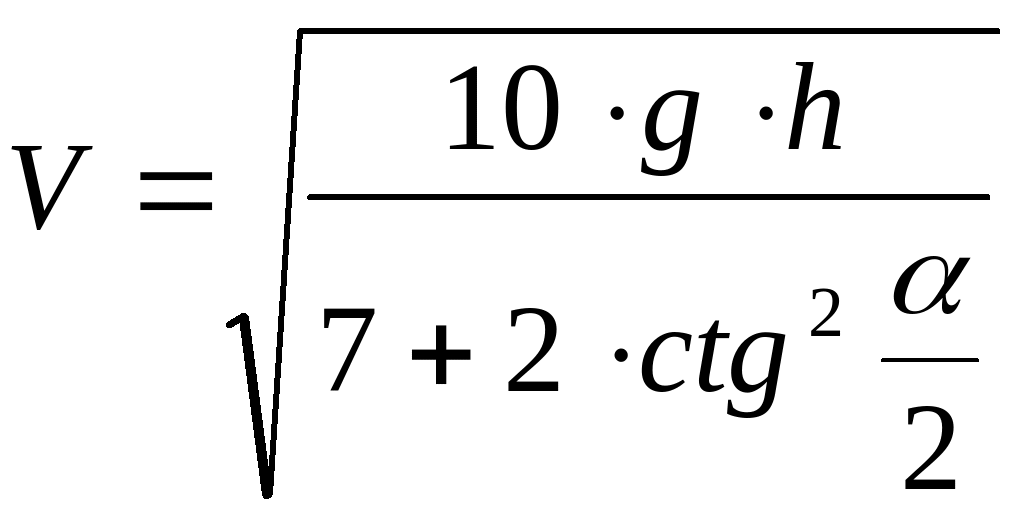 (7)
(7)
Это соотношение показывает возможность регулирования скорости скатывания шара по желобу не только значением высоты скатывания h, но и углом раствора желоба a. Максимальная скорость достигается при a = p (шар движется по наклонной плоскости). При a » 0 (шар движется между двумя почти параллельными друг другу вертикальными плоскостями) скорость поступательного движения падает почти до нуля - шар только вращается, оставаясь почти на месте. В данной конструкции угол a = 90°, поэтому
![]() (8)
(8)
Эта формула является одной из двух рабочих формул для данной работы. По ней можно теоретически вычислить скорость, которую будет иметь шар, скатывающийся по желобу с высоты h и построить график зависимости скорости от высоты различных точек желоба.
