2.6 Составление математической модели системы автоматического управления

В инженерной практике для оценки статических и динамических свойств системы используются математические модели, устанавливающие взаимосвязь входных и выходных величин в установившихся (статических) и переходных (динамических) режимах, получаемые аналитически или экспериментально.

Математическую модель системы автоматического управления удобно представить в виде алгоритмической структурной схемы. Алгоритмическая структурная схема САУ температурой животноводческого помещения представлена на рисунке 2.5.

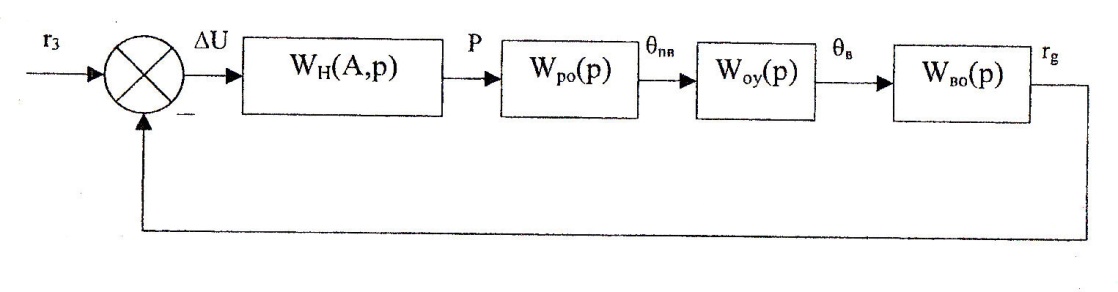
- передаточная функция регулятора;

- передаточная функция электрокалориферной установки РО; - передаточная функция объекта; - передаточная функция датчика - воспринимающего органа.

Рисунок 2.5 - Алгоритмическая структурная схема САУ

В рассматриваемой системе в качестве регулятора используется двухпозиционный регулятор с зоной нечувствительностью. Ширина зоны нечувствительности выбирается из задания на проектирование (Δ_Р < Δ_п).

Учитывая, что регулятор имеет нелинейную статическую характеристику система в целом является нелинейной.

Регулирующий орган - электрокалориферная установка имеет передаточную функцию:

.

Передаточная функция объекта управления имеет вид:

.

И передаточная функция воспринимающего органа

.

Специфической особенностью нелинейной системы является режим автоколебаний.

Автоколебания в нелинейных системах являются устойчивым режимом работы. Например, в системе автоматической стабилизации температуры с нелинейным управляющим устройством. При анализе нелинейных систем решают следующие задачи:

- отыскание возможных состояний равновесия системы и оценка их устойчивости.

- определение параметров автоколебаний и их связь с параметрами системы.

Обычно в нелинейной системе содержится один существенно нелинейный элемент.

Линейная часть включает в себе все элементы с линейными или линеаризованными характеристиками и может иметь структуру любой сложности.

В рассматриваемой системе нелинейным элементов является двухпозиционный регулятор температуры, а линейная часть включает регулирующий орган (РО), объект управления (ОУ) и воспринимающий орган (ВО).

2.7 Анализ устойчивости системы

Одной из важнейших характеристик системы автоматического управления является устойчивость. Неустойчивая система неработоспособна, т.е. она не способна выполнить функции управления и может привести управляемый объект в аварийное состояние. Любая практическая система должна быть устойчивой.

Условия устойчивости реальных систем автоматического управления сформулировал А.М Ляпунов:

1) Если линейная САУ устойчива, то устойчива и реальная САУ, при этом никакие отброшенные при линеаризации члены не могут изменить её устойчивость.

2) Если линейная САУ неустойчива, то неустойчива и реальная САУ, при этом никакие отброшенные при линеаризации члены не могут изменить её устойчивость.

В связи с этим необходимо убедиться в устойчивости линейной части системы с передаточной функцией.

.

Объединив два звена с чистым запаздыванием, получим

.

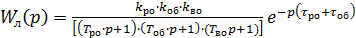Когда в контуре системы управления присутствует звено запаздывания, то характеристическое уравнение системы будет трансцендентным, решение которого связано с большими трудностями. Поэтому в практических расчетах трансцендентную передаточную функцию раскладывает в ряд Пада. Учитывая только два или три члена ряда, приближенно заменяют её дробной рациональной функцией [6]:

.

Такая замена дает удовлетворительное приближение, если частота входного сигнала:

, (рад/с).

Другим способом приближенной аппроксимации звена запаздывания является представление его в виде последовательного соединения нескольких инерционных звеньев первого порядка с одинаковыми постоянными времени

T_i = τ/n:

.

Учитывая, что для рассматриваемом в курсовом проекте системе не требуется высокая точность аппроксимации, звено с запаздыванием заменим одним инерционным звеном с передаточной функцией:

.

Соответственно, передаточная функция линейной части системы соответствует следующему выражению:

.

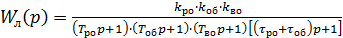Обозначим сумму .

Запишем передаточную функцию линейной части в стандартной форме:

,

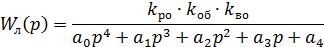
где

.

Используя критерии Гурвица или Рауса, определим устойчивость линейной части системы. Расчет рассмотрим при определении устойчивости на примере конкретной системы. При условии устойчивости линейной части системы можно переходить к определению устойчивости системы в целом.

Для определения устойчивости нелинейных систем применяется метод гармонической линеаризации (наряду с другими методами).

Метод гармонической линеаризации является приближенным методом, который позволяет определить условия возникновения и параметры автоколебаний.

При высоком порядке характеристического полинома системы этот метод требует значительных вычислений. Расчет упростится, если линейную часть системы, которая является по отношению к регулятору обобщенным статическим объектом с самовыравниванием, представим последовательно соединенными апериодическим звеном первого порядка и звеном с чистым запаздыванием [1, 3, 11]:

^,

где

Численные значения , , определим при рассмотрении примера конкретного объекта:

- В результате такого обобщения получаем нелинейную систему с двухпозиционным регулятором и объектом управления, для исследования которой применим метод гармонической линеаризации.

- Сущность метода заключается в замене существенного нелинейного элемента, эквивалентным линейным звеном.

- Условием эквивалентности служит равенство амплитуд и фаз выходного сигнала эквивалентного звена и первой гармоники выходного сигнала реального нелинейного элемента.

- Гармоническая линеаризация принципиально отличается от обычной линеаризации, так как коэффициенты линеаризованного элемента непостоянны и зависят от амплитуды входного сигнала. Коэффициенты гармонической линеаризации зависят от вида нелинейности и приведены в литературе [1.14].

Например, передаточную функцию двухпозиционного регулятора с зоной нечувствительности можно определить из выражения:

где и - коэффициенты линеаризации при А > а.

;

,

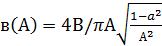где и - параметры статической характеристики регулятора (нелинейного элемента).

Заменяя на получаем выражение для АФЧХ нелинейного элемента

^.

Когда линейная часть системы описывается уравнением высокого порядка или содержит запаздывание для определения параметров автоколебаний, используется критерий Найквиста. Условием существования автоколебаний является равенство:

или ,

где - АФЧХ всех линейных звеньев системы, а правая часть - обратная характеристика нелинейного элемента с противоположным знаком.

Данное уравнение удобно решать графически. Для этого необходимо построить АФЧХ линейной части и обратную характеристику нелинейного элемента в одной системе координат.

В точках пересечения кривых определяют параметры автоколебаний. На кривой определяет частоту автоколебаний , на кривой – амплитуду автоколебания

Факт устойчивости или неустойчивости режима автоколебаний устанавливают при помощи следующего правила: если точка на кривой , близкая к точке пересечения, но сдвинутая в направлении возрастания параметра , не охватывается характеристикой , то автоколебания устойчивы, если же охватывается, то автоколебания неустойчивы.