2 Методика выполнения курсовой работы

2.1 Свойства объектов управления

Управляемый объект - основной элемент системы автоматического управления, в котором при помощи технических средств автоматизации осуществляется заданный алгоритм функционирования.

В состав объекта может входить набор машин для выполнения технологического процесса, а также внешняя среда, если она влияет на процесс управления. На объект действуют управляющие и возмущающие воздействия. Управляющие воздействия возникают в результате операций управления, которые стремятся приблизить процесс к заданному режиму работы.

Возмущающие воздействия, наоборот, удаляет процесс от заданного режима, стремятся вывести из установившегося состояния.

Чтобы обосновать выбор регулятора или управляющего устройства, необходимо знать статические и динамические характеристики объекта. Математическая модель может быть получена аналитическим или экспериментальным методом [1,2,3,12].

В основе аналитического исследования объектов управления лежит энергетический или материальный баланс. Для большинства объектов управления достаточно определения двух обобщенных координат, из которых одна характеризует поток вещества или энергию (входная), а другая (выходная) - параметр, определяющий результаты процесса. Такие объекты называют простыми одноемкостными объектами. Они могут быть описаны линейными дифференциальными уравнениями первого порядка, в которых третьей переменной является время. Виды дифференциальных уравнений, описывающих процессы, наиболее часто встречающиеся в сельскохозяйственном производстве в простых объектах управления приведены [1].

Процессы, протекающие в простых объектах управления, могут описаны в общем виде следующим выражением:

,

где L - часть объекта, неизменная во времени;

Y - управляемая величина;

X - входное воздействие.

На основании закона сохранения энергии можно записать, что

,

где Q_п, Q_р - входящие и выходящие потоки энергии или вещества.

Для установившегося режима .

Если объект вывести из состояния покоя, появляется возмущение ΔQ:

.

В общем случае входящий и выходящий потоки являются нелинейными функциями управляемой величины. Применив для их линеаризации разложение в ряд Тейлора, получаем:

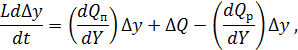
где .

Обозначив и , получим уравнения в относительных (безразмерных) единицах:

.

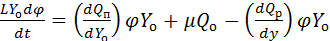Разделив это уравнение по и перегруппировав составляющие, получим:

.

Обозначив - время разгона, время, необходимое для заполнения емкости объекта поступающим веществом или энергией.

- коэффициент самовыравнивания (безразмерная величина).

С учетом обозначения получим:

.

Это уравнение было получено А. Стодолой.

Если разделить уравнение Стодолы на ( ), то получим стандартную форму дифференциального уравнения объекта:

,

где - постоянное времени объекта;

- коэффициент передачи объекта.

Передаточная функция объекта в операторской форме:

Проанализируем свойства одноемкостного объекта в зависимости от коэффициента самовыравнивания.

1) . Объект называют статическим, устойчивым, обладает свойством самовыравнивания;

2) . Объект не обладает свойством самовыравнивания, и его принято называть статическим неустойчивым объектом, т.е. при отсутствии вмешательства извне объект теряет управление;

3) . Объект лишен свойств самовыравнивания и называется астатическим объектом. Выходной параметр объекта управления растет безгранично по линейному закону.

Теплотехнические объекты сельскохозяйственного назначения относится к статистическим объектам с самовыравниванием, имеющий S-образную характеристику.

Для практических расчетов систем управления такими объектами S-образную кривую переходного процесса (см.рисунок 2.1) достаточно охарактеризовать следующими параметрами, определенными непосредственно по графику: передаточным коэффициентом , постоянной времени и полным запаздыванием .

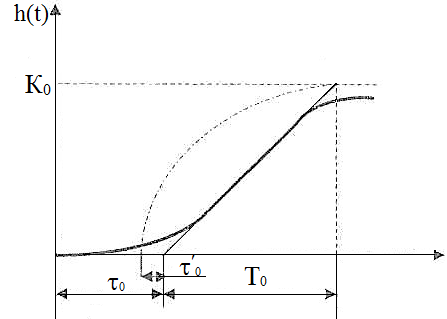
Рисунок 2.1 - Переходная характеристика объекта

S-образную характеристику можно заменить экспонентой с запаздыванием.

Передаточная функция объекта:

.

Постоянную времени объекта и запаздывания объекта определяются из следующих выражений [6]:

_о; .

При выполнении курсового проекта не ставится задача строгого определения параметров объекта управления. Поэтому принимаем упрощенную методику расчета характеристик животноводческого помещения. Обобщенным показателем является тепловая характеристика помещения , которая определяется по формуле [1,13]:

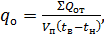, (кДж/м³ °С ч),

где - суммарное количество теплоты кДж/ч;

- объем помещения, м³;

- температура внутри помещения, °С;

- температура наружного воздуха, ºС.

Суммарное количество теплоты для отопления помещения можно вычислить из выражения:

Объем помещения вычисляется по формуле:

,

где - удельный объем помещения, м³/гол.

Численные значения, соответствующие , , , , , берутся из задания по курсовому проектированию.

Коэффициент теплопотерь определяется по формуле:

, (кДж/ч °С) или .

Теплоемкость животноводческого помещения определяем из формулы:

,

где - удельная теплоемкость воздуха ( , кДж/кг °С);

- плотность воздуха ( кг/м³) при температуре 20°С;

- объем помещения, м³.

Постоянное времени животноводческого помещения определяется по формуле [12]:

, час, или , мин.

Запаздывание в объекте можно вычислить

Конкретное значение приведено в задании.

Для принятой модели объекта как последовательное соединение апериодического звена первого порядка и звена с чистым запаздыванием определяем передаточное

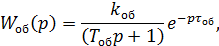
где - коэффициент передачи объекта в относительных единицах равен единице;

- постоянное времени;

– запаздывание.

Если в выражение для определения Т_об подставить выражение для определение А и С, то получим:

час.

Постоянное времени для модели объекта (животноводческого помещения) можно определить из значения удельной тепловой характеристики помещения в часах или в секундах.

Постоянное времени животноводческого помещения Т₀ будет равно:

или .