3.5 Расчет прочности балки по нормальному сечению
Определяем положение нейтральной оси из условия (при γs4 = 1)
(3.11)
,
следовательно, нейтральная ось проходит
в полке.
Граничное
значение
im=0,657.
Высоту сжатой зоны х находят по формуле :
(3.12)
.
Отношение x/d=126,35/1450=0,09<0,657.
Изгибающий момент, воспринимаемый сечением в середине балки, по формуле:
;
(3.13)
3.6 Расчет прочности наклонных сечений по поперечной силе
Максимальная поперечная сила у грани опоры V= 459,04 кН. Размеры балки у опоры: h=1600 мм; d=1600-150=1450мм; b=100 мм, B=340 мм на опоре.
Вычисляем проекцию расчетного, наклонного сечения на продольную ось с по ранее принятой последовательности коэффициент, учитывающий влияние свесов сжатой полки φf :
принимаем
=0,441.
Влияние продольного усилия обжатия:
N=Pmt= кН;
;
(3.14)
.
Принимаем
=0,5
параметр (1+
+
)
=(1+0,5+0,441)= 1,941>1,5, принимаем 1,5.
Вычисляем:
;
(3.15)
В расчетном сечении:
Vb=Vsw=Vsd/2 (3.16)
следовательно,
с=Bb/0,5Vsd=
.
Тогда
Vb=Bb/c=
;
поперечное армирование не требуется
по расчету.
Принимаем
для поперечных стержней арматуру
диаметром 8 мм класса S400
Asw
=
0,503 см2.
По конструктивным требованиям шаг
поперечных стержней S
должен
быть не более 1/3h
и
не более 500 мм; S-h/3
=160/3
533,3
мм, принимаем на приопорных участках
S=200мм.
Для средней половины пролета при назначаем шаг по конструктивным требованиям S=500 мм.
3.7 Расчет по образованию трещин
Если Mcr<M, то требуется производить расчет по раскрытию трещин.
В этом расчёте необходимо проверить раскрытие трещин в балке при эксплуатации.
Определяем момент трещинообразования
Мsd=
.
Mcr=
-
условие выполняется, следовательно
расчет по раскрытию трещин не требуется.
3.8 Расчет балки по деформациям
Максимальный прогиб в середине пролета свободно опертой однопролетной плиты, загруженной равномерно распределенной нагрузкой определяют по формуле:
(3.17)
В - изгибная жесткость железобетонного элемента, соответствующая изгибающему моменту Msd n;
leff −эффективный (расчетный) пролет элемента.
Коэффициент ак в формуле представляет собой постоянную интегрирования, зависящую от условий закрепления и схемы нагружения элемента. Значения этого коэффициента приведены в табл. 11.1 [10].
Жесткость железобетонного элемента, работающего без трещин, выражается в зависимости от длительности действия нагрузки и момента инерции сечения в стадии I напряженно-деформированного состояния и определяется по формуле:
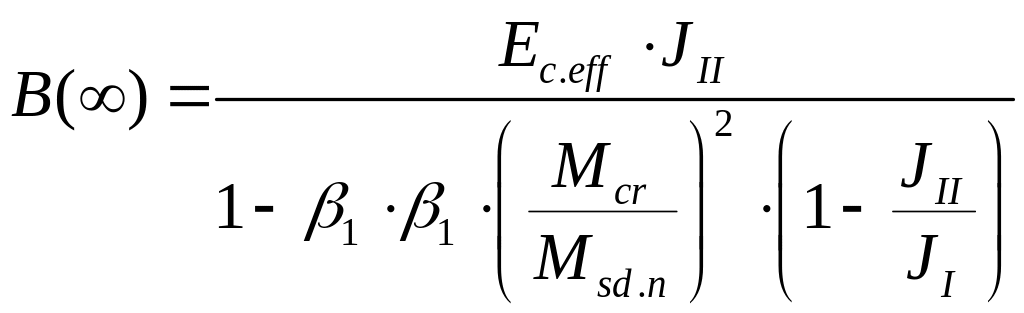(3.17)
Для прямоугольного сечения:
(3.18)
(3.19)
При
получим:
.
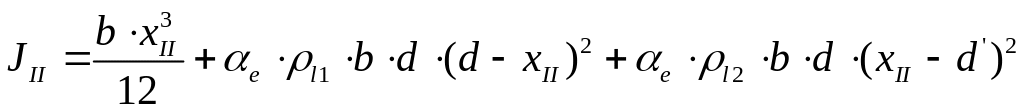(3.20)
При
получаем:
.
Жесткость сечения с трещиной:
.
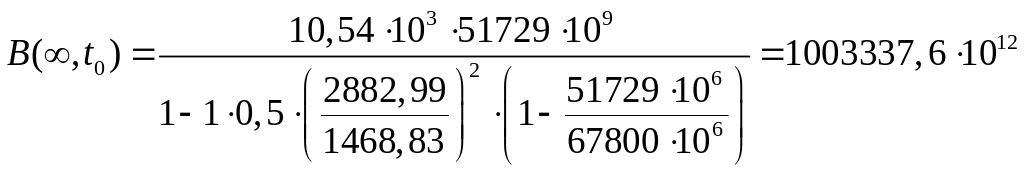Прогиб в середине пролета:
.
Допустимый прогиб:
.
.
Максимальный прогиб в середине пролета балки не превышает допустимый, т.е. проверка выполняется.