3.1 Определение нагрузок и усилий

Нагрузки на балку сведем в таблицу 3.

Вид нагрузки	Нормативная нагрузка, кН/м	Коэффициент надежности по нагрузке	Расчетная нагрузка
Постоянная От покрытия	2,625·7=18,375	-	3,754·7=26,278
От собственного веса	5,5	1,35	7,43
Всего	23,875	-	33,708
Временная Длительная	0,3·7=2,1	1,5	3,15
Кратковременная	0,7·7=4,9	1,5	7,35
Полная нагрузка:
Постоянная и длительная	25,975	-	36,858
Кратковременная	4,9	-	7,35
Полная	30,875	-	44,208

Расчетный пролет при опирании поверху равен:

Вычисляем изгибающие моменты и поперечные силы с учетом коэффициента надежности по значению γ_n=0,95:

Максимальный момент от полной расчетной нагрузки в середине пролета

Максимальный момент от полной нормативной нагрузки в середине пролета

Момент в наиболее опасном сечении в 1/3ролета от расчетной нагрузки равен

,

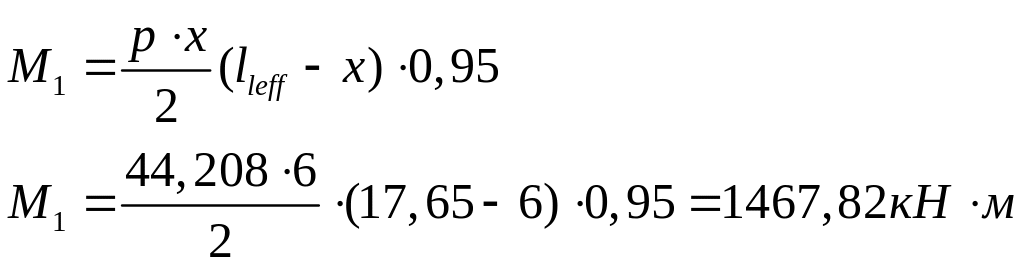где x=17.65∙0.35=6м.

Наибольшая поперечная сила от полной расчетной нагрузки

3.2 Предварительный расчет сечения арматуры

Определим сечение напрягаемой арматуры из условия обеспечения прочности.

(6,1)

где

В опасном сечении:

Ориентировочное значение сечения напрягаемой арматуры из условия обеспечения трещиностойкости:

(6,2)

Необходимое число проволоки 5 S1400 с A_st  0,196см ²:

Назначаем 82 5 S1200 с площадью сечения 16,072см². Площадь ненапрягаемой арматуры в сжатой зоне бетона принимаем конструктивно 2 18 S400 c площадью сечения 5,09см², тоже в растянутой зоне.

3.3 Определение геометрических характеристик приведенного сечения.

Рисунок 3.2- Расчетное сечение балки в середине пролета

Отношение модулей упругости

α = E_s / E_b = 18000 / 3400 =5,3

Приведенная площадь арматуры: см²;

см².

Площадь приведенного сечения балки в пролете:

мм².

Статический момент площади приведенного сечения относительно нижней грани:

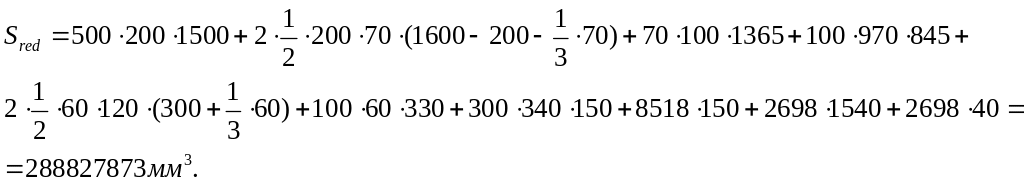
Расстояние от нижней грани до центра тяжести приведенного сечения:

(3.7)

мм.

То же , до верхней грани: у ₀ = 1600−848,21 = 751,79 мм.

Расстояние от точки приложения силы обжатия до центра тяжести приведенного сечения:

z_ср=у₀-с=848,21-150=698,21мм.

Момент инерции приведенного сечения относительно оси проходящей через центр тяжести сечения:

(3.8)

где − момент инерции рассматриваемого сечения относительно своего центра

тяжести;

−площадь сечения;

a_i - расстояние от центра тяжести рассматриваемой части сечения до центра

приведенного сечения;

Момент сопротивления приведенного сечения относительно нижней его грани:

(3.9)

мм³.

Расстояние от центра тяжести приведенного сечения до верхней ядровой точки:

мм,

где при , то .

Расстояние от центра тяжести приведенного сечения до нижней ядровой точ­ки:

мм,

где мм³.

Момент сопротивления сечения для нижней грани балки с учетом неупругих деформаций бетона:

(3.10)

где ;

;

; .

мм³.

Приближенно можно принять: W_pl = у∙W _red,

где у - коэффициент принимаемый для тавровых сечений с полкой в сжатой зоне;

у = 1,5; (для верхней грани балки), тогда :

мм³.

Момент сопротивления сечения для верхней грани балки с учетом неупругих деформаций бетона:

мм³,

где ;

; ; .

Можно принять:

мм³.