Метод неопределённых коэффициентов
(не содержит процесса интегрирования).
Этот метод применим только к линейным уравнениям с постоянными коэффициентами и только в том случае, когда его правая часть имеет специальный вид. По виду правой части уравнения записывают ожидаемую форму частного решения с неопределёнными коэффициентами, затем подставляют её в уравнение и из полученного тождества находят значения коэффициентов.
Рассмотрим различные виды правых частей уравнения
-
№
Правая часть
Частное решение
примечание
1
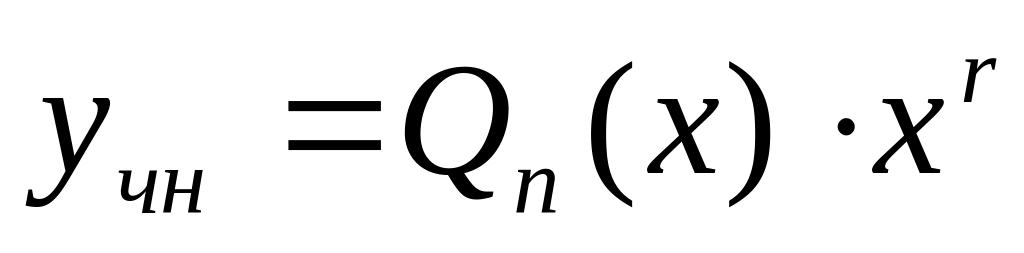
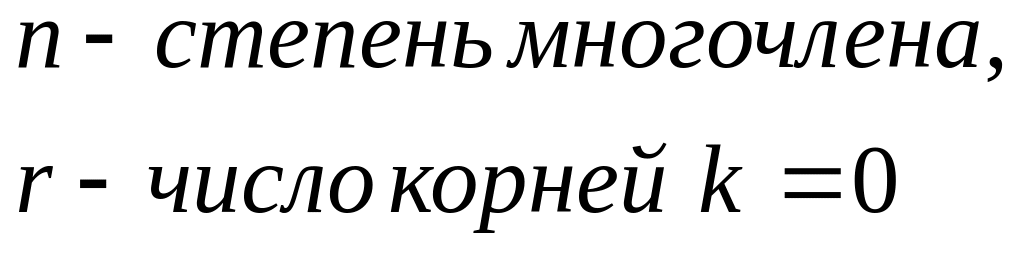
2
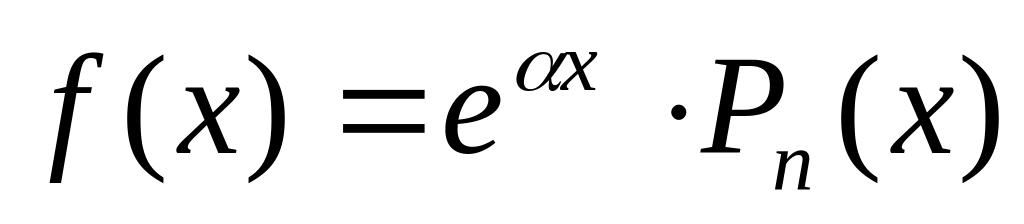
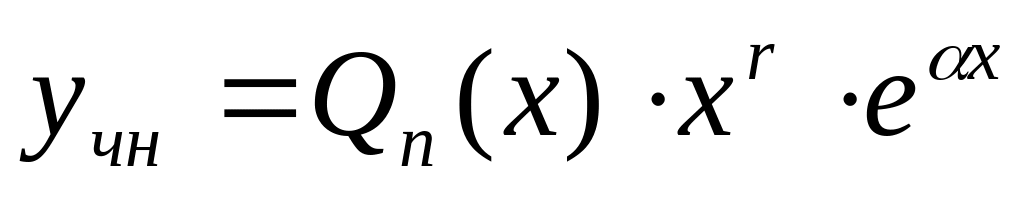
3
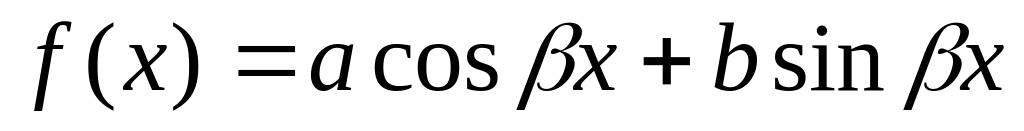
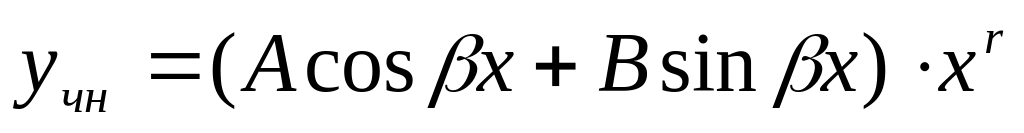
4
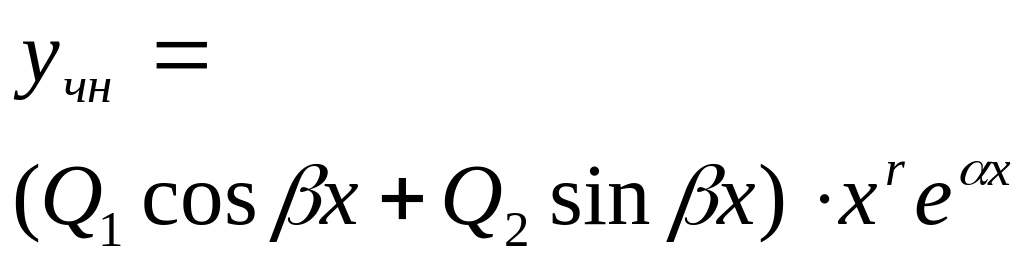
5
Пример 1. Найти
общее решение уравнения
.
Решение.
Характеристическое уравнение
имеет корни
,
следовательно, общее решение однородного
уравнения имеет вид:
.Так как ни один из корней характеристического
уравнения не равен нулю, то частное
решение ищем в виде
,
где А и В- неизвестные коэффициенты.
Дифференцируя дважды
и подставляя
в данное уравнение, найдём
.
Приравнивая коэффициенты при одинаковых
степенях в обеих частях равенства:
находим:
.
Итак, частное
решение данного уравнения имеет вид
.
а его общее решение
.
Пример 2.
Найти общее решение уравнения
.
Решение.
Характеристическое уравнение
имеет корни
.
Тогда общее решение однородного уравнения
имеет вид
.
Так как среди корней характеристического
уравнения имеется только один корень
,
то
.
В данном случае
многочлен
первой степени. Поэтому частное решение
уравнения будем искать в виде
.
Дифференцируя дважды
и подставляя в
уравнение, получаем
Приравнивая
коэффициенты при одинаковых степенях,
получаем систему уравнений
.
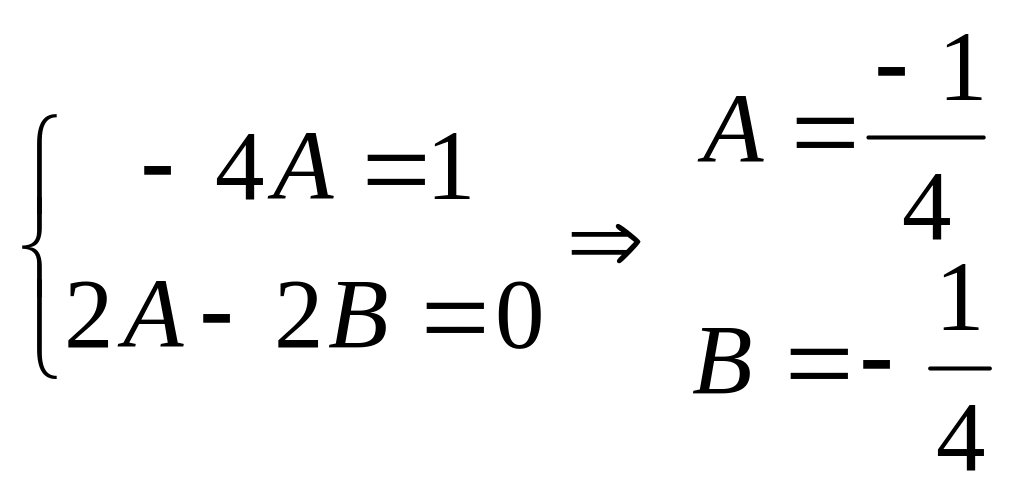Следовательно, частное решение уравнения
.
Тогда общее решение имеет вид
.
Пример 3.
Найти общее решение уравнения
Решение.
Характеристическое уравнение
имеет корни
Поэтому общее решение соответствующего
однородного уравнения
.
В правой части равенства
,т.е.
.
Так как
корень характеристического уравнения,
то
и частное решение ищем в виде:
Дифференцируя и подставляя в уравнение,
получаем:
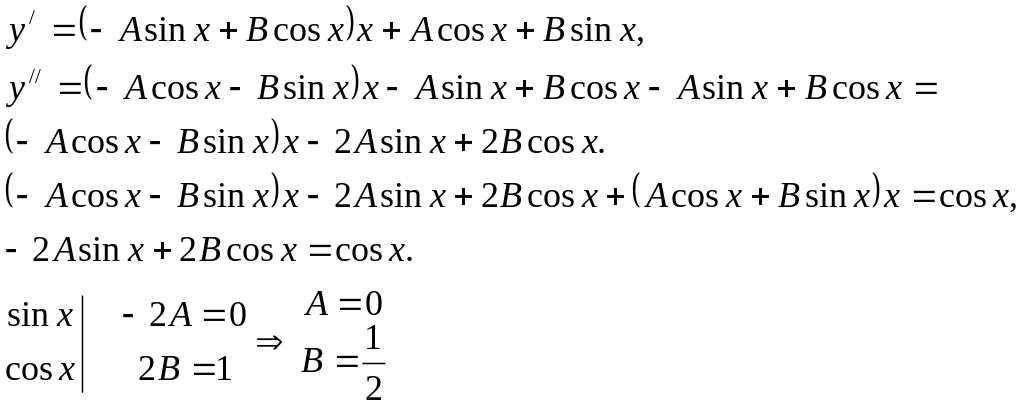
Таким образом,
частное решение
,
общее решение исходного уравнения
Пример 4. Найти
общее решение уравнения
.
Решение.
Характеристическое уравнение
имеет корни
,
тогда общее решение соответствующего
однородного уравнения имеет вид:
.
Так как
не является корнем характеристического
уравнения, то
и частное решение следует искать в виде
.
Дифференцируем:
Подставляя
в уравнение, получаем:
частное решение
;
следовательно, общее решение уравнения
Пример 5. Найти
общее решение уравнения
.
Решение.
Характеристическое уравнение
имеет
корни:
,
поэтому общее решение соответствующего
однородного уравнения
.
Правая часть уравнения
, следовательно, частное решение ищем
в виде
.
Дифференцируем:
Подставляя в
уравнение
,
получаем:
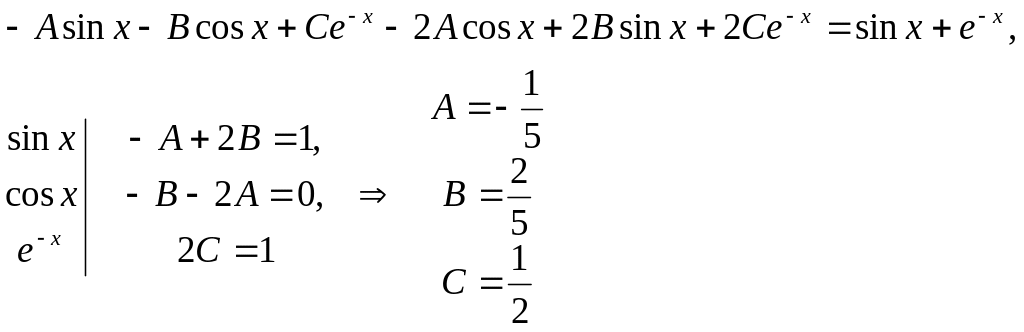
Таким образом,
частное решение исходного уравнения
имеет вид
,
а общее решение этого уравнения
.
Контрольная работа выполняется по пособию Зариповой З.Ф.
«Математика. Часть I. Методические указания по выполнению контрольных работ по дисциплинам «Математика», «Высшая математика» для бакалавров всех направлений и форм обучения»