
- •Кафедра «Теория вероятностей и математическая статистика» Вопросы и задачи по теории вероятностей
- •Кафедра «Теория вероятностей и математическая статистика»
- •Вопросы и задачи по теории вероятностей
- •125468, Ленинградский пр-т, 49
- •2. Схема Бернулли
- •3. Дискретные случайные величины
- •4. Непрерывные случайные величины
- •5. Начальные и центральные моменты случайных величин
- •6. Случайные векторы
- •7. Предельные теоремы теории вероятностей
- •● Центральная предельная теорема
- •Практические задания
- •1. Случайные события
- •2. Дискретные случайные величины
- •3. Непрерывные случайные величины
- •4. Случайные векторы
- •Ответы к задачам
4. Непрерывные случайные величины
● Функция распределения и функция плотности непрерывной случайной величины
Дайте определение непрерывной случайной величины . Чему в этом случае равна вероятность
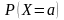 ,
где
– определенное число? Следует ли
из равенства
,
где
– определенное число? Следует ли
из равенства
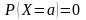 для непрерывной случайной величины
,
что событие
для непрерывной случайной величины
,
что событие
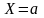 никогда не наступает?
никогда не наступает?
Какое распределение называется абсолютно непрерывным? Что такое плотность распределения и какова ее связь с функцией распределения? Может ли абсолютно непрерывная случайная величина иметь разрывную функцию плотности
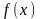 ?
Ответ обоснуйте.
?
Ответ обоснуйте.
Перечислите основные свойства функции плотности вероятности. Чем объясняется название «плотность вероятности»?
● Основные законы распределения непрерывных случайных величин
Как определяется показательный закон распределения с параметром
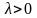 ?
Укажите формулу для функции плотности
,
найдите соответствующую функцию
распределения
и постройте графики функций
и
.
?
Укажите формулу для функции плотности
,
найдите соответствующую функцию
распределения
и постройте графики функций
и
.Как определяется равномерный закон распределения на отрезке
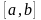 ?
Укажите формулу для функции плотности
,
найдите соответствующую функцию
распределения
и постройте графики функций
и
.
?
Укажите формулу для функции плотности
,
найдите соответствующую функцию
распределения
и постройте графики функций
и
.Возможно ли равномерное распределение на всей числовой оси? Чему равна вероятность
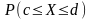 для равномерно распределенной на
отрезке
для равномерно распределенной на
отрезке
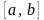 случайной величины
?
Рассмотрите случаи: 1)
случайной величины
?
Рассмотрите случаи: 1)
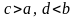 и 2)
и 2)
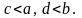
Как определяется нормальный закон распределения на прямой? Укажите формулу для функции плотности , найдите соответствующую функцию распределения и приведите формулу для вычисления вероятности
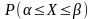 .
.Запишите плотность распределения нормальной случайной величины , для которой
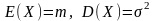 .
Как изменится график плотности
распределения, если: а) увеличится
.
Как изменится график плотности
распределения, если: а) увеличится
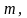 б) увеличится
б) увеличится
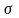 ?
?
● Числовые характеристики непрерывных случайных величин
Как вычисляется математическое ожидание в случае распределения с плотностью
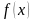 ?
Может ли для какой-либо абсолютно
непрерывной случайной величины не
существовать математического
ожидания? Ответ обоснуйте.
?
Может ли для какой-либо абсолютно
непрерывной случайной величины не
существовать математического
ожидания? Ответ обоснуйте.
Как вычисляется дисперсия в случае распределения с плотностью ? Докажите, что для случайной величины с плотностью
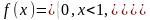 дисперсия
дисперсия
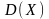 не существует, а математическое
ожидание
не существует, а математическое
ожидание
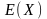 существует.
существует.
● Основные характеристики типичных непрерывных распределений
Выведите формулы для математического ожидания и дисперсии случайной величины, равномерно распределенной на отрезке

Объясните (с доказательством) вероятностный смысл параметра в формуле
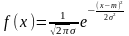 для функции плотности случайной
величины
,
распределенной по нормальному
закону.
для функции плотности случайной
величины
,
распределенной по нормальному
закону.
Объясните (с доказательством) вероятностный смысл параметра в формуле для функции плотности случайной величины , распределенной по нормальному закону.
Докажите, что для случайной величины, распределенной по показательному закону с параметром
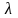 ,
математическое ожидание
,
математическое ожидание
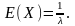
Случайная величина равномерно распределена на отрезке
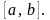 Можно ли для любых
и
Можно ли для любых
и
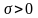 подобрать параметры
и
так, чтобы
подобрать параметры
и
так, чтобы
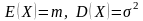 ?
Как по
и
найти
и
?
?
Как по
и
найти
и
?
Что такое правило
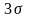 для нормального распределения?
Верно ли, что для любой нормальной
случайной величины
существует отрезок
для нормального распределения?
Верно ли, что для любой нормальной
случайной величины
существует отрезок
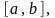 для которого
для которого
 ?
Ответ обоснуйте.
?
Ответ обоснуйте.
