5. Построение графика переходного процесса и оценка качества

скорректированной системы

5.1 Моделирование системы на авм

Исходным выражением для моделирования является передаточная функция разомкнутой скорректированной системы W_ск(р).

Составим аналоговую модель системы на основании моделей типовых динамических звеньев. Схема модели приведена на рисунке 7.

Рассчитаем машинные коэффициенты модели.

Машинные коэффициенты преобразующего элемента:

Машинные коэффициенты корректирующего устройства:

Машинные коэффициенты управляющего устройства:

Машинные коэффициенты исполнительного устройства:

Машинные коэффициенты объекта управления:

Рисунок 7 - Схема аналоговой модели системы

2. Моделирование системы на цвм

Для цифрового моделирования системы используем среду Matlab приложение Simulink. Схема цифровой модели системы, составленная из типовых звеньев библиотеки Simulink, показана на рисунке 8.

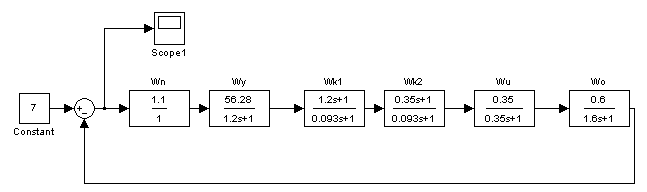
Рисунок 8 - Схема цифровой модели системы

Результатом моделирования является переходная характеристика по каналу ошибки x_з – ε , регистрируемая прибором Scope1. Переходная характеристика системы по каналу ошибки x_з – ε приведена на рисунке 9.

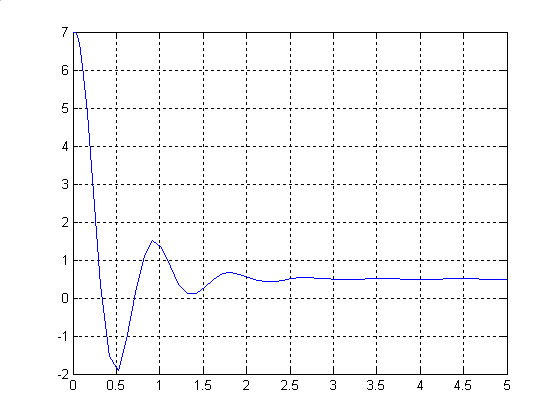
Рисунок 9 - Переходная характеристика системы по каналу ошибки x_з – ε

По графику переходного процесса определим перерегулирование, время переходного процесса и сравним полученные значения с заданными.

ε(∞)=0,5 - что удовлетворяет заданию

6. Вычисление и минимизация квадратичной интегральной оценки

при типовом воздействии

Исходным выражением для вычисления квадратичной интегральной оценки является передаточная функция замкнутой скорректированной системы по каналу х_з-ε при единичном ступенчатом воздействии (то есть принимаем задающее воздействие Х_з(t)=1, а следовательно Х_з(р)=1/р). Запишем эту передаточную функцию:

Раскроем скобки и приведем передаточную функцию к стандартному виду:

Подставим в формулу численные значения:

Запишем выражение для изображения переходной составляющей сигнала ошибки:

Так как передаточный коэффициент разомкнутого контура k_рк≥10 допускается упростить выражение для изображения переходной составляющей с учетом следующих условий:

k_рк+1=k_рк и k_рк-1=k_рк

Преобразуем выражение для изображения переходной составляющей сигнала ошибки, используя вышеприведенные условия:

=

Для вычисления квадратичной оценки по изображению используют равенство Парсеваля, которое имеет вид:

Где

Таким образом коэффициенты d_i и v_i равны:

d_o =0,0138 v_o =0,00019

d₁ =0,306 v₁ =-0,143

d₂ =1,786 v₂ =3,19

d₃ = k_рк

Составим определитель Δ по правилу составления определителя Гурвица

Определитель _v составляем из определителя  путем замены коэффициентов верхней строки на коэффициенты ₀, ₁ и ₂.

Вычисляем квадратичную интегральную оценку:

Задаваясь численными значениями k_рк, составляем таблицу зависимости квадратичной интегральной оценки от коэффициента k_рк, которая приведена ниже.

Таблица 3. – Расчетные данные для построения кривой зависимости интегральной оценки от передаточного коэффициента разомкнутого контура

kрк	Qкв
0	∞
1	1,039
2	0,63
5	0,37
8	0,325
10	0,317
10,5	0,366
10,56	0,3165
11	0,31,68
12	0,3174
20	0,39
24	0,47

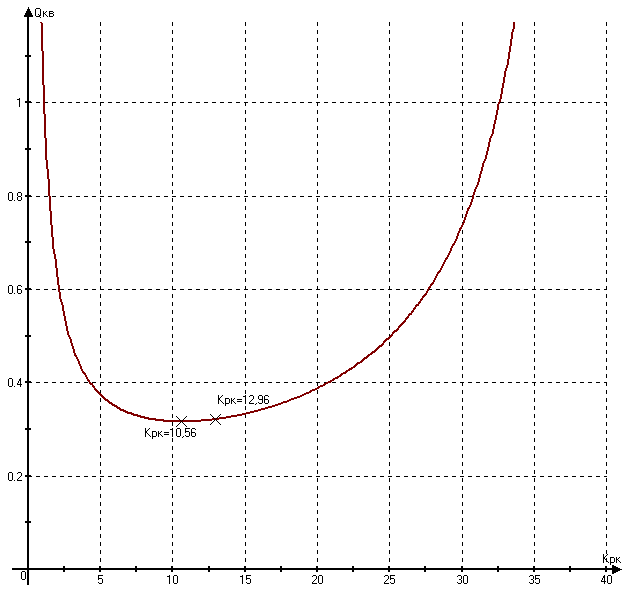
Рисунок 9 - Кривая зависимости интегральной оценки от передаточного коэффициента разомкнутого контура

Из рисунка 9 видно, что оптимальным значением k_рк является k_рк=10,56. При данном значении коэффициента разомкнутого контура система будет работать в оптимальном режиме, обеспечивая минимальную площадь под графиком переходного процесса.

Теперь перейдем от коэффициента k_рк к передаточному коэффициенту k_у. Для этого воспользуемся следующей формулой:

При коэффициенте k_рк=12,96 и квадратичной интегральной оценке равной Q=0.3218 передаточный коэффициент управляющего устройства k_у.= 56,28.

Вывод: В этом разделе с помощью квадратичной интегральной оценки получили оптимальное значение передаточного коэффициента управляющего устройства (k_у=45,8). Этот коэффициент получился меньше, чем тот, что был выбран в разделе 2 (k_у=56,28). Следовательно, при выборе этого коэффициента точность системы в установившемся режиме увеличится, но могут получиться более колебательные переходные процессы.