3. Расчет корректирующего устройства

Для построения ЛАЧХ исходной нескорректированной системы вычисляем частоты среза ω_ср и lgω_ср а также логарифм передаточного коэффициента lg k .

ω_ср1 =1/1.6=0.625 lgω_ср1 =-0.204

ω_ср2 =1/1.2=0.833 lgω_ср2 =-0.079

ω_ср3 =1/0.35=2.857 lgω_ср3 =0.456

lgk = lg 13 = 1.114 20lgk = 22.27

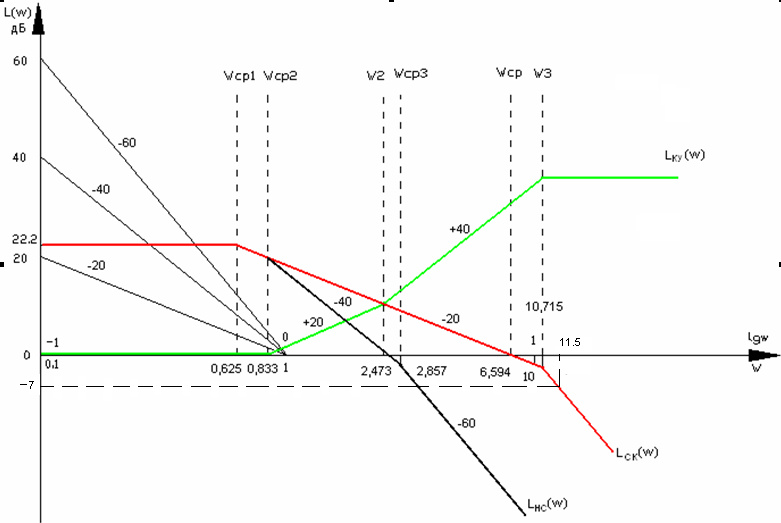
Рисунок 4. – Логарифмические амплитудно-частотные характеристики разомкнутого контура нескорректированной системы, скорректированной системы и корректирующего устройства

Для построения среднечастотного участка ЛАЧХ желаемой системы по заданным показателям качества (σ = 35%, t_п =2с, M=1.6) вычисляют его параметры.

lgω_ср=0.819

lgω₂=0.39

lgω₃=1.03

По вычисленным параметрам строится среднечастотный участок ЛАЧХ желаемой системы. Так как СЧ-участок ЛАЧХ не доходит до искомой ЛАЧХ продляем его до сопряжения с ней.

Из ЛАЧХ желаемой системы вычитаем ЛАЧХ исходной системы и получаем ЛАЧХ последовательного корректирующего устройства.

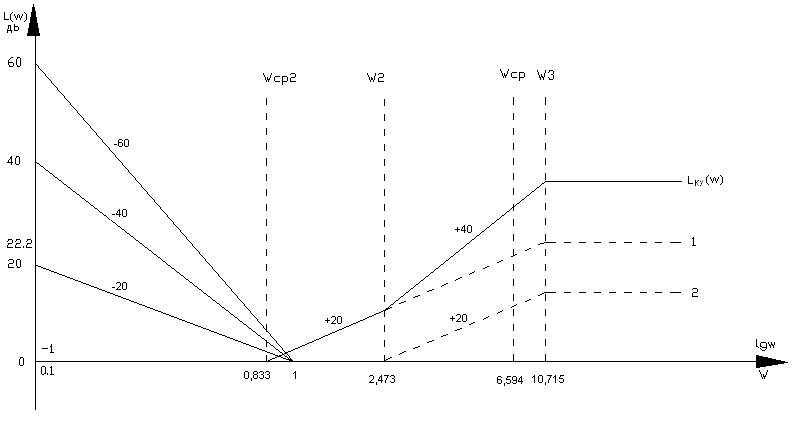
Рисунок 5 – Логарифмическая амплитудно-частотная характеристика корректирующего устройства

По виду ЛАЧХ выбираем два последовательно соединенных интегро-дифференцирующих звена с преобладанием дифференцирования. Принципиальная схема корректирующего устройства приведена на рисунке 6.

Рисунок 6 – Принципиальная схема корректирующего устройства

Пусть R₁=1МОм , R₃=1МОм , тогда

T₃=R₁C₁

T₃=R₃C₂

Запишем передаточную функцию скорректированной системы:

=

Заменяем р на jω:

Вычислим значение фазы на частоте среза φ(ω_ср) (значение частоты ω_ср = 6,594).

φ(ω_ср)=

Находим запас устойчивости системы по фазе.

Методом подбора найдем ω_π , при которой φ(ω_π) = 180^о.

При ω_π =10 φ(ω_π)=172,2^о

ω_π =12 φ(ω_π)=183,3^о

ω_π =11,5 φ(ω_π)=180,7^о

Чтобы определить запас устойчивости системы по амплитуде необходимо на ЛАЧХ скорректированной системы отметить частоту ω_π =11,5 и определить на этой частоте запас амплитуды.

Как видно из рисунка 4 запас устойчивости по амплитуде ΔL=7дБ.

Вывод: В разделе 2 было доказано, что нескорректированная система при увеличенном коэффициенте k_у была не устойчива. В данном разделе, введя корректирующее устройство и проанализировав ЛАЧХ уже скорректированной системы можно видеть, что скорректированная система устойчива и имеет запасы устойчивости по амплитуде и фазе:

ΔL=7дБ

4. Построение области устойчивости скорректированной системы

Исходным выражением для построения области устойчивости является характеристическое уравнение замкнутого контура скорректированной системы. Запишем это характеристическое уравнение:

Подставим в формулу выражение для передаточной функции разомкнутого контура.

Заменяем р на jω.

Объединим действительную и мнимую составляющие выражения:

Приравняем к нулю действительную и мнимую части:

Упорядочим систему уравнений относительно параметров k_рк и T_o :

Решим эту систему уравнений методом Крамера.

Подставим значения коэффициентов в выражения k_рк и Т_о .

=

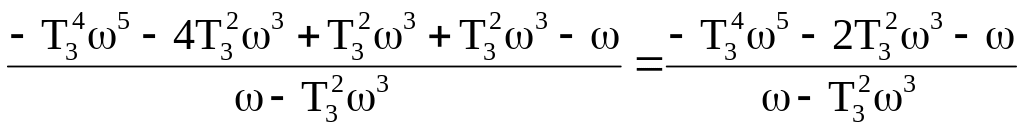
Так как область устойчивости надо строить в плоскости параметров k_П и T_О, то сделаем переход от коэффициента k_рк к коэффициенту k_и .

С учетом этого запишем уравнение k_рк относительно нужного нам параметра k_и .

k_и

Задаваясь значениями частоты ω от 0 до ∞, составляем таблицу 3, получаем данные для построения границы области устойчивости системы в плоскости двух параметров k_и и T_о .

Таблица 3. – Расчетные данные для построения границы области устойчивости системы

ω	kи	To
0	-0,027	-1,186
5	-0,05	-0,024
8	-0,14	-0,41
10	-0,65	-1,33
10,6	-2,92	-5,52
10,8	57,74	59,92
11	2,8	4,58
12	0,56	0,78
14	0,28	0,27
15	0,24	0,2
18	0,21	0,1
20	0,21	0,08
25	0,24	0,04
30	0,29	0,03
40	0,44	0,01
∞	∞	0

Используя данные таблицы 2, построим область устойчивости скорректированной системы в плоскости двух параметров k_и и T_о. Область устойчивости приведена на рисунке 5.

Дополним кривую D-разбиения особыми прямыми, уравнения которых имеют следующий вид: a₀=0, отсюда T₀=0; a_n=0, отсюда 1+k_и =0

k_и = - = - = -0,03

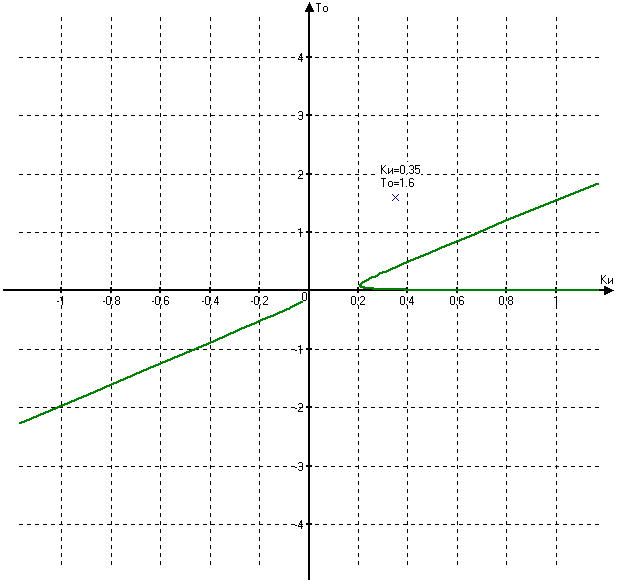
Рисунок 6. - Область устойчивости скорректированной системы в плоскости двух параметров k_и и T_о

Вывод: Как видно из рисунка 6 при коэффициенте k_и =0,35 и постоянной времени Т_о=1.6 система находится в области устойчивой работы, что означает правильность расчета корректирующего устройства. Таким образом, при заданных настройках системы автоматического регулирования, удовлетворяющих требованиям точности, система устойчива.