3. Повышение условного предела текучести

при повторных нагружениях (наклеп)

Если при нагружении образца не был превышен предел упругости, то при разгружении все деформации полностью ис­чезнут и при повторном нагружении этот образец будет себя вести так же, как и при первом нагружении.

Если же образец был нагружен до напряжения, большего предела упругости, например до напряжения, соответствующего точке К диаграммы на рис. 2, то разгрузка пойдет по прямой КL, параллельной линии ОА. Упругая часть деформации (отре­зок LM) исчезнет, пластическая же часть деформации (отрезок OL) останется.

Если материал нагружать снова, то диаграмма пойдет по прямой LK до самой точки K. Остаточное удлинение при раз­рыве будет измеряться величиной отрезка LR, т. е. иметь мень­шую величину, чем при первичном однократном нагружении до разрыва. Линия нагрузки не совсем совпадает с линией разгрузки, но отклонение незначительно и его можно не учитывать. Следовательно, при повторных нагружениях образца, пред­варительно растянутого до возникновения в нем напряжений, больших предела текучести, предел пропорциональности повы­шается до того уровня, которого достигли напряжения при предшествующей нагрузке. Если между разгрузкой и повторным нагруженном был перерыв, то предел пропорциональности повы­шается еще больше.

Следует отметить, что диаграмма LKEN получаемая при повторном нагружении, не имеет площадки текучести, поэтому для образца, претерпевшего разгрузку и повторное нагружение, определяется условный предел текучести σ_0,2, который, оче­видно, выше предела текучести при первичном нагружении. В указанном смысле можно говорить о повышении предела текучести при повторном нагружении.

Явление повышения предела пропорциональности и сниже­ния пластичности материала при повторных нагружениях назы­вается наклепом. Наклеп во многих случаях является нежела­тельным явлением, так как наклепанный металл становится более хрупким.

Однако в целом ряде других случаев наклеп полезен и его создают искусственно, например, в деталях, подвергающихся воздействию переменных нагрузок.

Литература

Основная

1. Беляев Н.М. Сопротивление материалов, «Наука», М., 1976, [1], гл. I, §§1-5.

2. Дарков А.В., Шпиро Г.С. Сопротивление материалов, «Высшая школа», М., 1975, [2], гл. I, §§1.1-6.1.

3. Васильев В.З. Краткий курс сопротивления материалов с основами теории упругости, издание «Иван Феодоров», Санкт-Петербург, 2001г.

4. Смирнов А.Ф. Сопротивление материалов, «Высшая школа» М., 1975г.

Дополнительная.

1. Феодосьев В.И. Сопротивление материалов, «Наука», М., 1975г.

2. Таран В.И. Сопротивление материалов. Пособие по решению задач, издание «Демеу» Алматы, 1992, 204 с.

ЛЕКЦИЯ 5

Тема: Расчеты на прочность и жесткость при растяжении и сжатии

План лекции:

5.1 Общие методы расчета элементов конструкции:

1. Расчет по допускаемым напряжениям

2. Расчета по предельной нагрузке

3. Расчет по допускаемым перемещениям

5.2 Типы задач при расчете на прочность

5.3 Пример

1. Общие принципы расчета элементов конструкции

В результате расчета нужно получить ответ на вопрос, удовлетворяет или нет конструкция тем требованиям надеж­ности, которые к ней предъявляются. Для этого необходимо, прежде всего, сформулировать те принципы, которые должны быть положены в основу оценки условий достаточной надежности. Без этого анализ конкретной конструкции сам по себе не может иметь целевого назначения. Так, если в конструкции определяются напряжения, надо предвари­тельно четко представить себе, зачем это нужно и что с найденными напряжениями надлежит делать в дальнейшем. Точно так же, если определяется форма деформированного тела, надо заранее наметить путь дальнейшего использова­ния полученного результата в оценке надежности конструк­ции. Все эти вопросы находят свое решение в выборе общего метода расчета.

Наиболее распространенным методом расчета деталей машин и элементов сооружений на прочность является рас­чет по напряжениям. В основу этого метода положено пред­положение, что критерием надежности конструкции яв­ляется напряжение или, точнее говоря, напряженное состоя­ние в точке.

Рассмотрим стержень с выточкой, пред­ставленный на рис.1, а. Можно показать, что при растя­жении такого стержня напряжения в точках А, располо­женных у вершины выточки, будут заметно больше, чем для гладкого стержня, растянутого теми же силами (рис. 1, б).

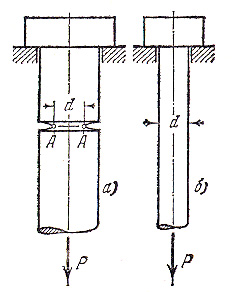
Рисунок 1

Если исходить из метода напряжений, то следует сделать вывод, что стержень с выточкой менее прочен, т. е. способен выдержать нагрузку меньшую, чем гладкий стержень. Од­нако это не всегда так. Для некоторых материалов, таких, как высокоуглеродистая сталь, стекло, камень и другие им подобные, стержень, имеющий выточку, действительно ока­зывается менее прочным, чем гладкий стержень. В случае, если оба стержня изготовлены из малоуглеродистой стали, меди, бронзы или алюминия, стержень с выточкой, вопреки ожиданиям, выдерживает не меньшую, а большую на­грузку. Таким образом, напряжения в точке не всегда и не полностью характеризуют условия разрушения кон­струкции.

В связи со сказанным в некоторых случаях используется метод расчета по разрушающим нагрузкам. В этом методе путем расчета определяются не напряжения, а наводится предельная нагрузка, которую может выдержать конструкция, не разрушаясь или не изменяя существенно свою форму. Предельная (разрушающая) нагрузка сопоставляет­ся с рабочей нагрузкой, и на основании этого делаются выводы о степени прочности конструкции в рабочих усло­виях. Этот метод обладает тем недостатком, что расчетное определение разрушающей нагрузки возможно только в наиболее простых конструкциях.

Методы расчета выбираются в зависимости от условий работы конструкций и требований, которые к ней предъяв­ляются. Если необходимо добиться наименьших изменений формы конструкции, например, при проектировании отража­теля прожектора или системы зеркал астрономического при­бора, производится расчет по допускаемым перемещениям, или, как говорят, расчет на жесткость. Это не исключает, понятно, одновременной проверки системы на прочность по напряжениям.

Наряду с упомянутыми методами расчета существуют многие другие методы, связанные с качественно отличными явлениями, такими, как устойчивость, эффект повторных нагрузок, динамическое воздействие и др.