Лекция №13 тема: касательные напряжения при изгибе

ПЛАН:

13.1 Определение касательных напряжений

13.2 Формула журавского

13.3 Касательные напряжения при поперечном изгибе балок различных сечений

1. Определение касательных напряжений

В общем случае изгиба (при поперечном изгибе) в попе­речных сечениях балки возникают изгибающие моменты и попе­речные силы. Наличие изгибающего момента связано с возни­кновением в поперечных сечениях балки нормальных напряже­ний, для определения которых можно пользоваться формулой (4) (см. лекцию №10).

Наличие поперечной силы связано с возникновением каса­тельных напряжений в поперечных сечениях балки, а по закону парности касательных напряжений – и в ее продольных сечени­ях (рис. 1).

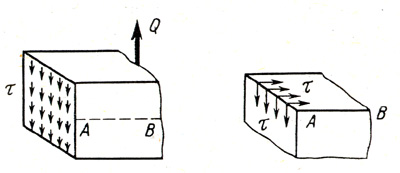
Рисунок 1

Для определения касательных напряжений рассмотрим вначале балку прямоугольного сечения небольшой ширины (рис.2).

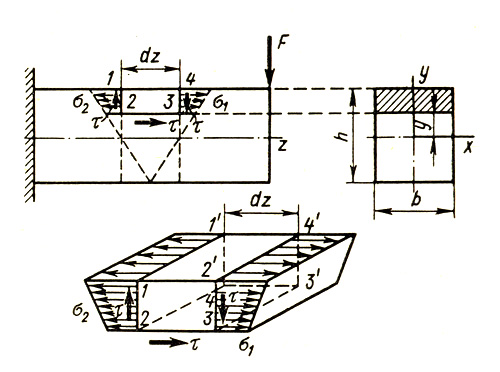
Рисунок 2

Вырежем из балки элемент длиной и шириной, равной ширине балки. На этот элемент действуют следующие силы: по грани 344'3' действуют нормальные напря­жения, которые согласно формуле (4) (см. лекцию №10) равны

(а)

где – изгибающий момент в сечении 344'3'.

Кроме того, в указанном сечении действуют неизвестные пока касательные напряжения τ, которые ввиду незначительной ширины сечения балки можно считать равномерно распреде­ленными по ширине сечения (гипотеза Журавского);

по грани 122'1' действуют нормальные напряжения

(б)

и касательные напряжения ;

по грани 322'3' действуют только касательные напряжения, по закону парности равные касательным напряжениям, действу­ющим по вертикальным граням.

Составим уравнение равновесия отсеченного элемента бал­ки. Спроецируем силы, действующие на элемент, на горизон­тальную ось. Очевидно, касательные усилия, действующие по вертикальным граням, в указанное уравнение не войдут.

Касательное усилие по грани 233'2' спроецируется в истин­ную величину τbdz. Нормальные усилия, действующие по грани 344'3', имеют равнодействующую

Нормальные усилия, действующие по грани 122'1', имеют равнодействующую

Интегралы должны быть взяты по площади отсеченной части, т. е. по площади граней 122'1' и 344'3'.

Используя, уравнение равновесия получаем

или

Используя выражения (а) и (б), имеем

Выражение представляет собой статический момент площади отсеченной части сечения относительно нейтраль­ной оси. Следовательно,

.

Но – приращение изгибающего момента на длине . Так что предыдущую формулу можно переписать в виде

откуда

.

Используя зависимость (2) (см. Лекцию№9), окончательно получаем

, (1)

где поперечная сила в рассматриваемом поперечном сечении балки,

статический момент (относительно нейтральной оси) отсеченной части поперечного сечения, расположенной по одну сторону от уровня, на котором определяются касательные напряжения,

момент инерции всего поперечного сечения относительно нейтральной оси,

ширина поперечного сечения балки на том уровне, на котором определяются касательные напряжения .