Лекция 9 тема: определение напряжений в стержнях круглого сечения

ПЛАН ЛЕКЦИИ:

9.1 Касательные напряжения при кручении круглого бруса 9.2 Деформации и перемещения при кручении валов 9.3 Пример определение напряжений в стержнях круглого сечения

Крутящие моменты представляют лишь равнодействующие внутренних сил. Фактически в попе­речном сечении скручиваемого стержня действуют непрерывно распределенные внутренние касательные напряжения.

Если на поверхности стержня круглого селения нанести прямоугольную сетку, то после деформации окажется (рис. 6):

1) прямоугольная сетка превратится в сетку, состоящую из параллелограммов, что свидетельствует о наличии касательных напряжений в поперечных сечениях бруса, а по закону парности касательных напряжений — и в продольных его сечениях;

2) расстояния между окружностями, например между / и //, не изменяется. Не изменятся длина стержня и его диаметр. Естес­твенно допустить, что каждое поперечное сечение поворачивает­ся в своей плоскости на некоторый угол как жесткое целое (гипотеза плоских и жестких сечений). На основании этой гипотезы можно считать, что радиусы всех поперечных сечений будут поворачиваться (на разные углы), оставаясь прямолиней­ными.

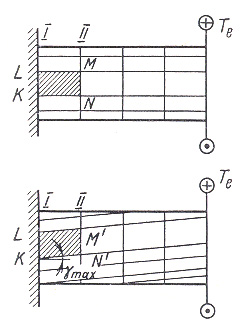
Рисунок 6

На основании этого можно принять, что при кручении в попе­речных сечениях стержня действуют только касательные напря­жения, т. е. напряженное состояние в точках скручиваемого стержня представляет собой чистый сдвиг.

Формулы, полученные на основе этого допущения, подтвер­ждаются опытами. Точка D переместится по дуге DD', точка С—по меньшей дуге СС' (рис.7).

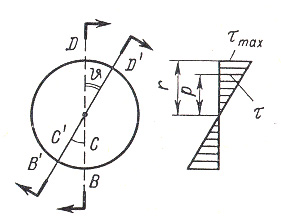
Рисунок 7

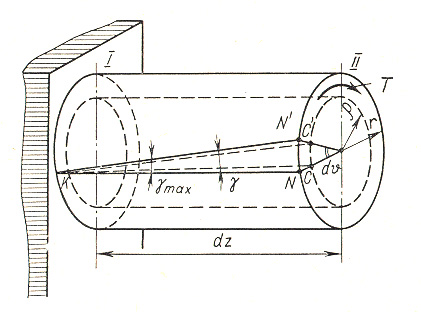
Рисунок 8

Для установления закона распределения касательных на­пряжений по поперечному сечению скручиваемого стержня рас­смотрим более детально деформации стержня (рис. 6 и 8). На рис.8 в более крупном масштабе изображена часть стерж­ня между сечениями I и II и показана одна сторона КN элемента KLMN (см. рис. 6).

Угол сдвига для элемента КLMN, лежащего на поверхности стержня, равен отношению отрезка N'N" к длине элемента dz (рис. 8);

γ_max=rdυ/dz . (1)

Выделяя мысленно из рассматриваемой части бруса цилиндр произвольного радиуса ρ и повторяя те же рассуждения, полу­чим угол сдвига для элемента, отстоящего на расстоянии ρ от оси стержня:

γ=ρdυ/dz. (2)

На основании закона Гука при сдвиге имеем

τ=Gγ=Gρdυ/dz . (3)

Как видим, при кручении деформации сдвига и касательные напряжения прямо пропорциональны расстоянию от центра тяжести сечения.

Эпюра касательных напряжений по поперечному сечению стержня представлена на рис. 7 справа.

В центре тяжести круглого сечения касательные напряжения равны нулю. Наибольшие касательные напряжения будут в точ­ках сечения, расположенных у поверхности стержня.

Зная закон распределения касательных напряжений, легко определить их из условия, что крутящий момент в сечении пред­ставляет собой равнодействующий момент касательных напря­жений в сечении:

, (4)

где τρdA — элементарный крутящий момент внутренних сил, действующих на площадке dА.

Подставив в (4) значение напряжений из формулы (3), получим

. (5)

Имея в виду, что

, (6)

где I_p— полярный момент инерции сечения, получим

dυ/dz=T/(GI_p). (7)

Подставляя значение dυ/dz в формулу (3), имеем

τ=Tρ/I_p. (8)

В частном случае, когда на стержень действует один внеш­ний скручивающий момент Т_е, (рис. 9), из условия равновесия отсеченной части стержня получим Т=Т_е.

Таким образом, окончательная формула для определения касательных напряжений при кручении имеет вид

τ=Tρ/I_p

Как видно из этой формулы, в точках, одинаково удаленных от центра сечения, напряжения τ одинаковы.

Наибольшие напряжения в точках у контура сечения

τ_max =Tr/I_p=T/W_p , (9)

где

W_p=I_p/r.

Геометрическая характеристика W_p называется полярным моментом сопротивления или моментом сопротивления при кру­чении.

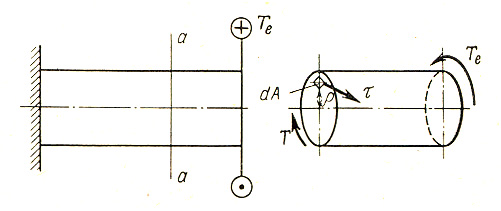
Рисунок 9

Для круглого сплошного сечения

W_p=I_p/r=(πd⁴)/(32d/2)=πd³/16≈0,2d³. (10)

Для кольцевого сечения

W_p=2I_p/D=[π(D⁴–d⁴)]/(16D)=(πD³/16)(1–c⁴) ≈0,2D³(1–c⁴),

где с=d/D.

Условие статической прочности вала при кручении имеет вид

τ_max=T/W_p≤ [τ] . (11)

Здесь [τ] — допускаемое касательное напряжение.

При действии статической нагрузки принимают (без учета концентрации напряжений и других факторов, снижающих про­чность) [τ] =(0,5÷0,6)[σ]. Кроме проверки прочности по этой формуле можно также подбирать диаметр вала или определять допускаемый крутящий момент при известных остальных величинах.

Допускаемый из условия прочности крутящий момент опре­деляют по формуле

[T]=W_p[τ]. (12)

При кручении во всех точках стержня, кроме точек его оси (в которых вообще не возникает напряжений), имеет место двухосное напряженное состояние — чистый сдвиг. При кручении материал у поверхности стержня напряжен силь­нее, чем материал, расположенный ближе к оси стержня. Таким образом, напряженное состояние является неоднородным. Если же скручивать тонкостенную трубу, то можно считать, что практически во всех точках ее стенки возникают одинаковые напряжения, т. е. в этом случае напряженное состояние будет однородным. Опыты с кручением таких труб используют обычно для изучения чистого сдвига и, в частности, для установления предела текучести при сдвиге τ_y.

3. ДЕФОРМАЦИИИ И ПЕРЕМЕЩЕНИЯ ПРИ КРУЧЕНИИ ВАЛОВ

Для вычисления деформаций вала при кручении воспользу­емся формулой (5):

dυ=Tdz/(GI_p). (13)

Деформация вала на длине z (взаимный угол поворота сечений) равна

. (14)

Если крутящий момент и величина GI_p, называемая жестко­стью вала при кручении, постоянны на всем участке интегриро­вания, то

υ=Tz/(GI_p). (15)

Аналогично, для вала длиной l получим

υ=Tl/(GI_p). (16)

Эта формула по своей структуре аналогична формуле для определения деформаций при растяжении — сжатии.

Угол закручивания, приходящийся на единицу длины, назы­вают относительным углом закручивания. Он равен

=υ/l=T/(GI_p). (17)

Для обеспечения требуемой жесткости вала необходимо, чтобы наибольший относительный угол закручивания не превос­ходил допускаемого, т. е.

=T/(GI_p)≤ . (18)

Эта формула выражает условие жесткости вала при круче­нии, В этой формуле — допускаемый относительный угол закручивания в радианах на единицу длины вала.

В большинстве случаев допускаемый относительный угол закручивания задают в градусах на 1 м длины, тогда взамен формулы (18) получим

(19)

Угол выбирают в зависимости от назначения вала и его размеров. Для валов средних размеров в «Справочнике машиностроителя» рекомендуется принимать допускаемый угол закру­чивания равным 0.5° на 1 м длины.

Из условия (19) можно определить диаметр вала по за­данной жесткости. Имея в виду, что I_p≈ 0.1d⁴, получаем

. (20)