БОУ ОО СПО
«Омский колледж транспортного строительства»
МАТЕМАТИКА
методические указания и задания
для студентов заочного отделения
по выполнению контрольной работы
Омск
2013
БОУ ОО СПО
«Омский колледж транспортного строительства»
МАТЕМАТИКА
методические указания и задания
для выполнения контрольной работы
для самостоятельной работы студентов I курса
заочного отделения всех специальностей
(кроме специальности 230103 )
Омск 2013
Одобрена цикловой комиссией общеобразовательных дисциплин |
Составлена в соответствии с Государственными требованиями к минимуму содержания и уровню подготовки выпускников для специальностей технического профиля
«____» ___________________2013г. |
Составитель: Глушко М.Л. – преподаватель Омского колледжа транспортного строительства.
Пособие предназначено для студентов III курса заочного отделения всех специальностей (кроме специальности 230103) для подготовки и выполнения контрольной работы по математике.
Данное издание содержит методические указания по изучению тем, которые лежат в основе выполнения задач контрольной работы, а также непосредственно сами задания работы и некоторые приложения.
Разработаны с учетом Государственных образовательных стандартов среднего профессионального образования.
I. Введение
Данное пособие по математике предназначено для подготовки и выполнения студентами III курса заочного отделения контрольной работы. Составлено в соответствии с программой и обеспечивает реализацию Государственных стандартов в части государственных требований к минимуму содержания и уровню подготовки выпускников средних профессиональных учебных заведений.
В результате изучения дисциплины студент должен
иметь представление:
о роли и месте знаний по дисциплине «Математика» при освоении смежных дисциплин по выбранной специальности и в сфере профессиональной деятельности;
о методах решения некоторых практических задач с использованием аппарата математического анализа;
о методах сбора и обработки статистической информации;
знать:
базовые понятия дифференциального и интегрального исчисления;
структуру дифференциального уравнения и способы решения простейших видов уравнений;
базовые понятия теории вероятностей и выборочного метода математической статистики;
уметь, используя справочный материал:
найти производную элементарной функции;
вычислить определенный интеграл;
решить дифференциальное уравнение 1-го порядка с разделенными переменными;
выполнить статистическую точечную оценку параметров распределения.
Контрольная работа служит основанием для получения зачета или допуска к экзамену по математике в соответствии с учебным планом.
II. Содержание учебной дисциплины
Раздел 1. Элементы математического анализа
Функция.
Предел функции. Непрерывность функции
Производная и дифференциал функции
Приложение производной и дифференциала к решению прикладных задач
Интеграл и его приложения
Дифференциальные уравнения
Раздел 2. Основные понятия теории вероятностей и математической статистики.
Элементы теории вероятностей.
Элементы математической статистики.
III. Методические указания по изучению отдельных тем дисциплины
Функция. Область определения функции
Прежде всего, надо познакомиться с основными понятиями: функция, область определения функции, множество значений, а также способы задания функции. Для этого необходимо изучить §14 - 17 (с. 103 – 119), учебника «Математика» Н.В. Богомолова (в дальнейшем [2] по списку литературы представленному в конце данного пособия), особое внимание необходимо уделять свойствам различных функций, а также подробно разобранным примерам. После теоретической подготовки следует решить задачу №1 контрольной работы по своему варианту. Пример решения задач такого типа представлен ниже.
Пример: Найти область определения
функции:
.
Решение: Найдем область определения
каждого из слагаемых; общая часть этих
областей и будет областью определения
данной функции. Для первого слагаемого
имеем: так как квадратные корни определены
только для неотрицательных чисел, то
,
решив данное неравенство, имеем:
.
Для второго слагаемого дробное выражение
определено для всех
,
кроме тех, при которых знаменатель
обращается в нуль. Таким образом,
или
.
Следовательно, область определения
- все
,
кроме точки
.
Предел функции
При изучении данной темы необходимо в начале познакомится с понятиями «числовая последовательность» и «предел переменной величины», изучив §42 (с.193 – 202), учебника [2]. Затем перейти непосредственно к вопросу вычисления предела функции. Данный материал подробно изложен в §43 (с.202 – 208), учебника [2]. Особое внимание необходимо уделить теоремам о пределах и их следствиям. После изучения данных вопросов можно приступить к выполнению задачи №2. Также решать задачи на вычисление пределов можно, используя приложения производной и правило Лопиталя, изучив темы 3 и 4.
Пример: Вычислить предел:
.
Решение:
Пределы числителя и знаменателя при
равны нулю:
,
.
Разложим квадратный трехчлен в числителе
на линейные множители по формуле
,
где
и
- корни трехчлена. Для этого решим
квадратные уравнения: х2 – 5х + 6 =
0. В знаменателе дроби вынесем за скобки
общий множитель 3х и теперь дробь можно
сократить на
.
Затем вместо х подставим значение равное
3 и вычислим предел. Получим:
Производная функции. Приложения производной
Данная тема предполагает сначала изучение материалов, связанных с понятием производная, представленных в §45 - §47 (с.211 – 223), учебника [2]. Особое внимание необходимо уделить формулам дифференцирования и вытекающим из них следствиям. Очень подробно рассмотрены примеры нахождения производной в учебнике Богомолов Н.В. «Практические занятия по математике» (в дальнейшем [3] по списку литературы представленному в конце данного пособия) на стр.96 -98. Для вычисления производной сложных функций можно воспользоваться примерами, разобранными в этом же учебнике на стр.99 и затем приступить к выполнению задачи №3.
При изучении приложений производной необходимо опираться на теоретические основы, представленные в §48 - §49, (с.224 – 227), учебника [2], а также материал по приложению производной к исследованию функций, который содержится в Главе8 учебника [3] , там же очень подробно разобраны примеры решения задач аналогичных тем, что представлены в контрольной работе.
После изучения материалов данной темы студенты решают задачу №4 по своему варианту. Ниже представлены примеры решения задач такого типа.
Пример 1. Найти производную функции:
.
Решение:
Применив формулы нахождения производной,
имеем
При навыке дифференцирования промежуточные действия обычно выполняются в уме и поэтому в подобных примерах сразу же записывается окончательный результат дифференцирования.
Пример 2. Найти производную функции:
Решение:
Заменив, кубический корень дробным
показателем и по формуле
найдем производную степени:
Пример 3. Точка движется прямолинейно
по закону
.
Найти значения скорости и ускорения в
момент времени
.
Решение:
Найдем скорость движения точки в любой
момент времени
:
.
Вычислим скорость движения точки в момент :
(м/с).
Найдем ускорение движения точки в любой момент времени :
.
Вычислим ускорение движения точки в момент времени :
(м/с2).
Пример 4. Найти промежутки монотонности
функции:
.
Решение:
Находим производную:
,
затем приравниваем ее к нулю и находим
критическую точку. Имеем
.
Вся числовая ось разбивается этой точкой
на два интервала. Определим знак
производной в каждом из интервалов,
если он отрицательный, значит, функция
на этом интервале убывает, если
положительный, то возрастает.
Последующие нахождения представим в таблице:
-
x
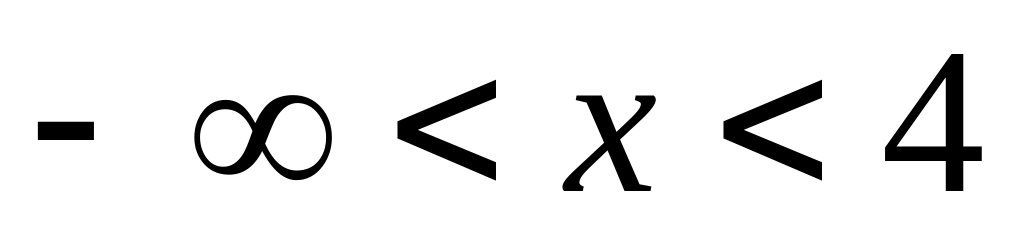
4
-
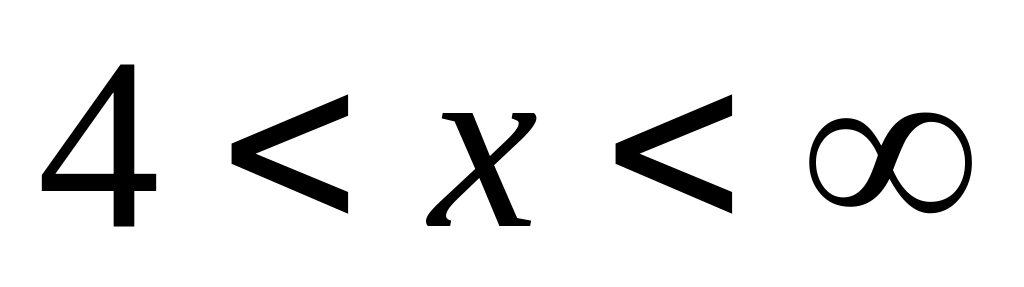
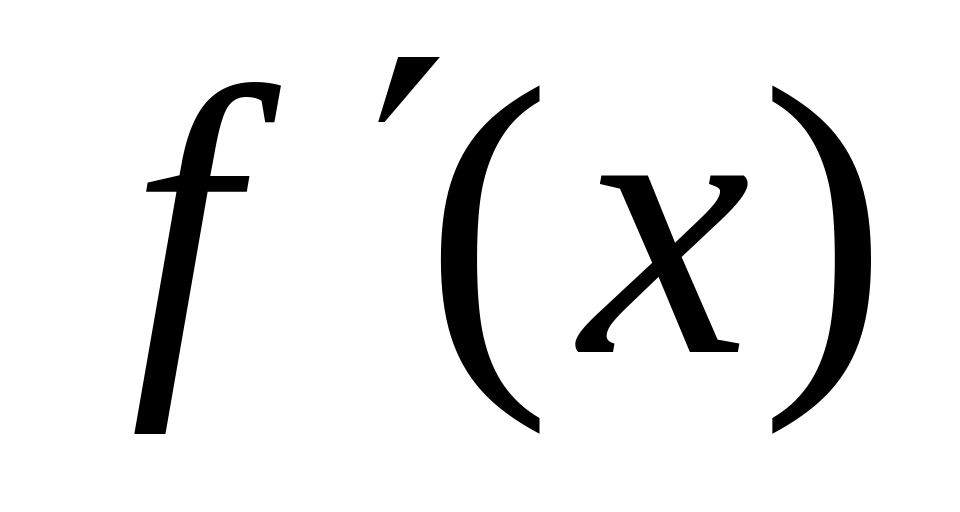
0
+
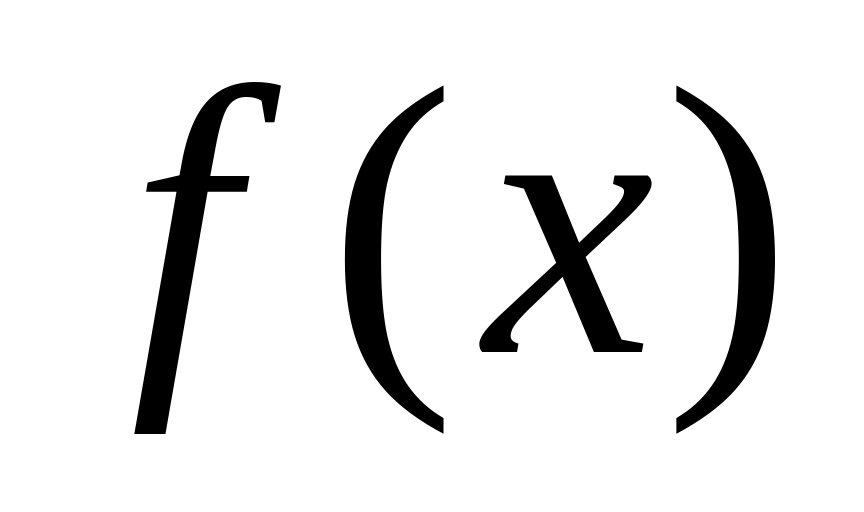
Таким образом, данная функция в промежутке убывает, а в промежутке возрастает. Ее график представлен на рис.1.
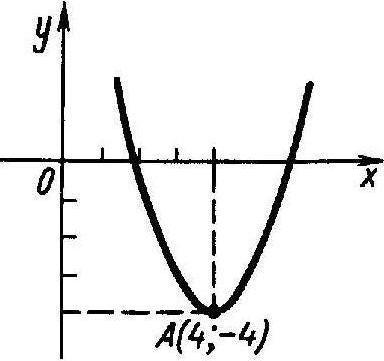
рис. 1
Пример 5. Исследовать на экстремум
функцию:
.
Решение:
Первоначально ход решения полностью
повторяет предыдущую задачу. Находим
;
.
Для наличия экстремума необходимо,
чтобы производная функции меняла знак
при переходе через критическую точку.
Если происходит смена знака с «+» на «
- », то данная критическая точка является
максимумом, если же знак меняется с «-»
на «+», тот точкой минимума. Составим
таблицу:
x |
|
|
|
|
+ |
0 |
- |
|
|
Максимум
|
|
Графиком функции
служит парабола, изображенная на рис
2.
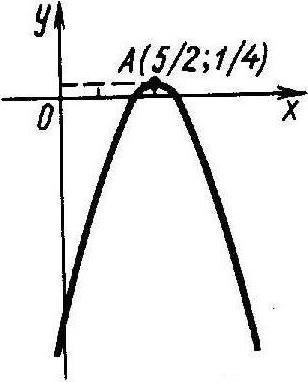
рис. 2
Неопределенный интеграл
Изучение неопределенного интеграла начинается с понятия первообразной функции и ее неоднозначности. Затем непосредственно вводится понятие неопределенного интеграла, при этом необходимо в записи неопределенного интеграла четко уметь разделять подынтегральную функцию и подынтегральное выражение. После этого изучаются основные свойства неопределенного интеграла и формулы интегрирования. Данный материал представлен в §62 - §63 (с.261 – 268), учебника [2], здесь же представлены приемы интегрирования и рассмотрены конкретные примеры.
После изучения материалов данной темы можно приступить к решению задачи №5 по своему варианту. Ниже представлены примеры решения задач такого типа.
Пример 1. Найти интеграл:
.
Решение:
Используя свойства 3 и 4 и формулы №1 и
№2 (приложение 2), имеем
.
Постоянная интегрированная С равна
алгебраической сумме трех постоянных
интегрирования, так как каждый интеграл
имеет свою произвольную постоянную:
.
Пример 2. Найти интеграл:
.
Решение:
В этом случае необходимо раскрыть скобки и только после этого приступить непосредственно к нахождению интеграла. При этом решение выглядит следующим образом:
.
Пример 3. Найти интеграл:
.
Решение:
Постоянный множитель выносим за знак
интеграла и формуле №8 (приложение 2)
получаем:
.
Определенный интеграл и его приложения
Данная тема предполагает знакомство с понятием определенного интеграла через изучение теоремы Нютона – Лейбница, которую рассматривают без доказательства. Теоретические основы этой темы изложены в §66 (с.271 – 278), учебника [2]. При рассмотрении материалов данного параграфа особое внимание необходимо уделить алгоритму нахождения определенного интеграла и внимательно разобраться с вопросами нахождения площадей криволинейных трапеций через определенный интеграл.
Для лучшего усвоения материалов темы рекомендуется подробно рассмотреть решения различных примеров, изложенные ниже в данном пособии, а также в главе 13 §1 (с.212 – 218), учебника [3]. После этого можно приступить к решению задачи №6 контрольной работы.
П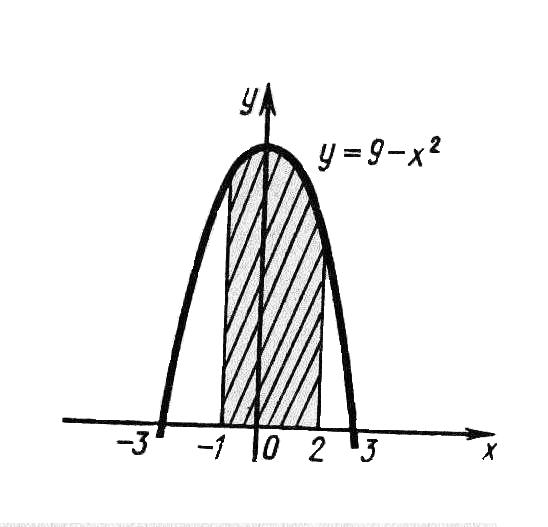
ример
1. Вычислить площадь криволинейной
трапеции, ограниченной осью Ох, прямыми
,
и параболой
(рис.3).
Решение.
Так как на отрезке [-1, 2] функция
принимает положительные значения, то
для вычисления искомой площади S
воспользуемся формулой
.
Другими словами, решение сводится к
вычислению неопределенного интеграла:
.
Применяя формулу Ньютона – Лейбница,
находим рис.3
(кв.ед.).
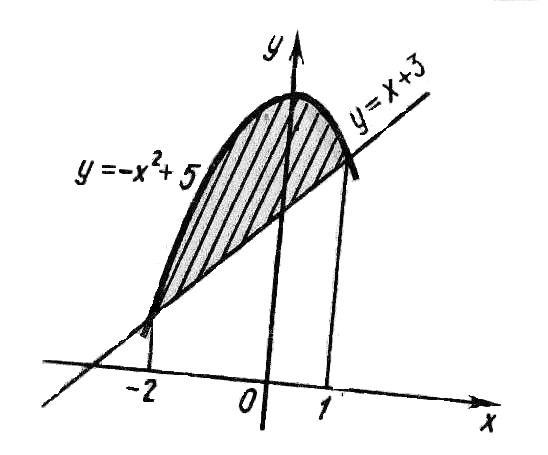
Пример 2. Вычислить площадь
криволинейной трапеции, ограниченной
линиями
и
.
Решение.
Найдем абсциссы точек пересечения
параболы
и прямой
.
Для этого решим систему
откуда
,
.
Найдем площадь
фигуры, ограниченной параболой
,
прямыми
,
и
(рис.4).
Получим
(кв.ед.).
Найдем площадь
фигуры, ограниченной прямыми
,
,
и
:
(кв.ед.).
Площадь искомой фигуры есть
(кв.ед.).
рис. 4
Элементы теории вероятностей
Данная тема содержит два раздела. Первый знакомит с основными понятиями комбинаторики: размещения, перестановки, сочетания. По окончанию изучения данного раздела надо знать понятие факториала числа и основные формулы комбинаторики. Данный материал описан в §93 (с.371 – 373), учебника [2]. Далее целесообразно перейти к изучению §94 (с.374 – 381), учебника [2]. Материал данного параграфа содержит описание таких понятий как событие; случайное, достоверное и невозможное событие. Далее вводится понятие вероятности и описываются теоремы сложения и умножения вероятностей.
В ходе изучения материалов данных параграфов необходимо подробно разбираться в решениях приведенных задач, а затем приступить к выполнению задачи №7 контрольной работы. Ниже приведены решения отдельных видов подобных задач.
Пример №1. Вычислить:
.
Решение:
Так как
,
,
то можно вынести за скобки общий множитель
3!
Ответ: 3.
Пример №2. Решить уравнение:
.
Решение:
Так как
,
то имеем
,
.
Ответ: .
Пример №3. В лотерее из 1000 билетов имеются 20 выигрышных. Вынимают наугад один билет. Чему равна вероятность того, что этот билет выигрышный?
Решение:
Общее число различных исходов есть
.
Число исходов благоприятствующих
получению выигрыша, составляет
.
Согласно формуле
,
получим
.
Пример №4. Из урны, в которой находятся 12 белых и 8 черных шаров, вынимают наудачу 2 шара. Какова вероятность того, что оба шара окажутся черными?
Решение:
Обозначим событие, состоящее в появлении
двух черных шаров, через
.
Общее число возможных случаев
равно числу сочетаний из 20 элементов
по два:
.
Число случаев
,
благоприятствующих событию
,
составляет
.
Находим вероятность появления двух черных шаров:
.