1.6.1. Трапеції, діагоналі яких взаємно перпендикулярні
У шкільному курсі
геометрії трапляються задачі на
рівнобічну трапецію, діагоналі якої
взаємно перпендикулярні. Учні, які добре
володіють методами розв’язування
геометричних задач, задають деякі
властивості такої трапеції. Наприклад:
1) діагоналі такої трапеції утворюють
кути по
з основами трапеції; 2) діагоналі трапеції
разом з її основами утворюють рівнобедрені
прямокутні трикутники; 3) довжина висоти
такої трапеції дорівнює довжині її
середньої лінії; 4) площа трапеції
дорівнює квадрату висоти або квадрату
її середньої лінії. Виникає запитання,
чи не має своїх властивостей нерівнобічна
трапеція
з перпендикулярними діагоналями?
Теорема. Якщо
діагоналі трапеції взаємно перпендикулярні,
то її висота є середнім геометричним
проекцій її діагоналей на будь-яку
основу, тобто виконується рівність:
,
де
-
довжина висоти трапеції;
,
- довжини проекцій діагоналей трапеції
на будь-яку її сторону.
Дано:
- трапеція;
;
;
;
.
Довести: .
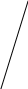
B
C
A
N
M
D
E
Мал.11.
I спосіб. Виконаємо
паралельне перенесення діагоналі
(мал.11.) на відрізок
,
що дорівнює меншій основі трапеції.
Оскільки в трикутнику
кут
- прямий, то висота
є середнім геометричним проекцій
катетів, тобто відрізків
і
.
Звідси випливає доводжувана рівність
:
.
II спосіб (без
додаткової побудови).
Трикутники
і
подібні,
оскільки вони прямокутні
.
Тому
,
або
.
Обернена теорема. Якщо висота трапеції є середнім геометричним проекцій діагоналей на будь-яку з її основ. То діагоналі такої трапеції взаємно перпендикулярні.
Дано:
- трапеція;
,
де
;
;
.
Довести: .
● У трикутнику
-
висота,
,
.
З умови випливає, що
.
Тому трикутники
і
подібні за двома пропорційними сторонами
і кутом між ними.
Отже
,
.
Маємо:
.