5. Теорема Фалеса. Середня лінія трикутника.

Дидактична мета: Ознайомити учнів з теоремою Фалеса, поняття середньої лінії трикутника та її властивостями, а також з їх застосуваннями.

Розвивальна мета: Розвивати інтерес до математики, зокрема на матеріалі її історії, математичну інтуїцію, логічне і, зокрема, дедуктивне мислення.

Завдання. Учні мають знати формулювання теореми Фалеса та означення і властивість середньої лінії трикутника; вміти доводити відповідні теореми та застосовувати знання до розв’язування задач.

Засоби навчання. Додатково до традиційних бажано використовувати кольорову крейду та нерозлінований папір.

Засвоєння теореми Фалеса ускладнюється її частиною, в якій доводиться, що коли на одній стороні кута взяти три точки , , і через них провести прямі, паралельні між собою, що перетинають другу сторону кута відповідно в точках , , то з умови, що точка лежить між точками і , випливає, що точка лежить між точками і . По-перше, це твердження для багатьох учнів буде з числа так званих «очевидних», а по-друге, доведення цієї частини теореми може відвернути увагу учнів від головного змісту висновку теореми.

З метою підвищення ефективності засвоєння учнями теореми Фалеса можна перед її доведенням нагадати зміст аксіоми про розбиття площини на дві півплощини і розв’язати такі вправи:

Дано кут і на його стороні вибираємо три точки , і таким чином, що точка лежить між точками і . Через мі точки проведено паралельні прямі, які перетинають другу сторону кута відповідно в точках , і . Доведіть, що точка лежить між точками і .

При обґрунтуванні способу ділення відрізка на рівних частин і при доведенні теореми про властивості середньої лінії трикутника можна запропонувати учням вправи:

1. Дано кут з вершиною в точці і на його стороні відкладено три рівні відрізки 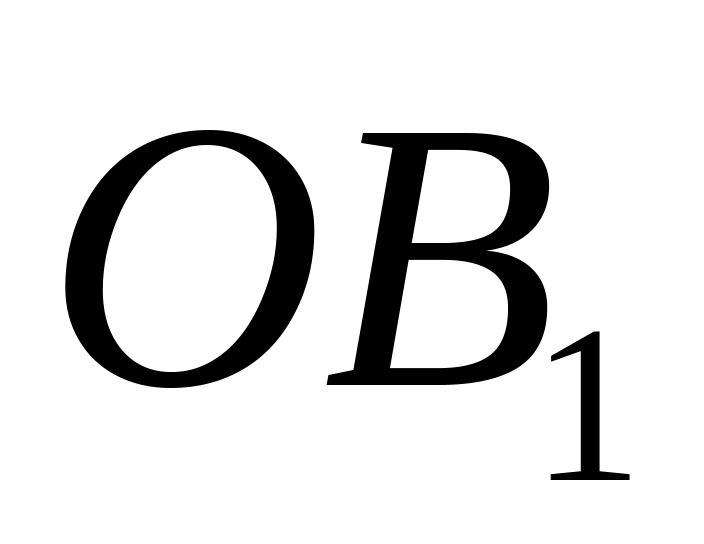, і 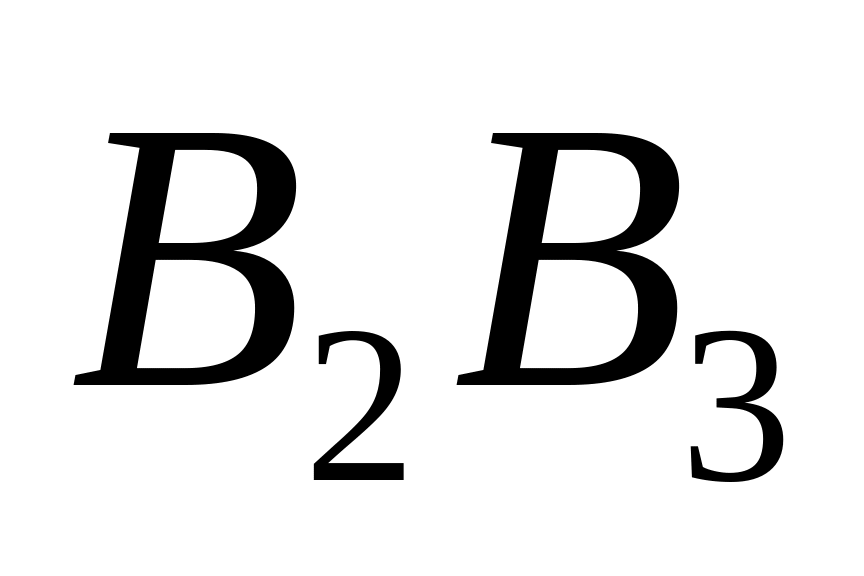, а на стороні вибираємо точку . Користуючись теоремою Фалеса, розділити відрізок на три рівні частини.

2. Дано відрізок . Розділіть його на три рівні частини.

3. Дано відрізок . Як розділити його на рівні частини?

4. Дано трикутник і його середня лінія з кінцями на сторонах і (мал.9.).

1. Проведіть через точку пряму, паралельну основі трикутника, і знайдіть точку її перетину зі стороною . У якій точці ця пряма перетинає сторону ?

2. Проведіть через точку пряму, паралельну стороні трикутника, і позначте буквою 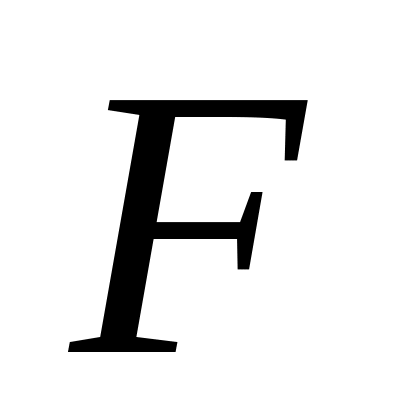точку її перетину з основою трикутника.

C

E D

A F B

Мал.9.

3. Порівняйте відрізки і .

4. Яким є чотирикутник ?

5. Порівняйте відрізки і .

1.6. Трапеція. Середня лінія трапеції.

Дидактична мета: Сформувати в учнів уявлення про трапецію, її види, середню лінію та її властивості.

Розвивальна мета: Розвивати інтелектуальні вміння систематизувати та узагальнювати набуті раніше знання, аргументувати свої дії.

Завдання. Учні мають знати означення трапеції, назви її елементів, види; вміти обґрунтовано виділяти трапеції серед інших чотирикутників; вміти застосовувати знання до розв’язування задач.

Засоби навчання. Таблиці, кольорова крейда.

Приступаючи до вивчення трапеції, треба, перш за все, показати цю фігуру на предметах навколишнього життя і на моделях: бічні грані зрізаної призми або піраміди, вигляд збоку торгівельного намету або сараю з односхилим дахом, моделі різних трапецій (картонних або дротяних) і тому подібне Вчитель нагадує, як була отримана трапеція з довільного чотирикутника. Учні формулюють означення трапеції, особливо підкреслюючи родову ознаку (це — чотирикутник) і дві видові відзнаки (дві сторони паралельні, а інші дві — непаралельні), креслять цю фігуру, позначають вершини її. Викладач повідомляє, що сторони трапеції мають особливі назви: АД і ВС — основи (АД || ВС), АВ і СД — бічні сторони (АВ СД).

На малюнку спочатку з'ясовується, що трапеція володіє всіма властивостями будь-якого опуклого чотирикутника, а саме: у ній можна провести дві діагоналі, кожна з яких ділить фігуру на два трикутники, а обидві — на чотири трикутники; сума внутрішніх кутів дорівнює 360⁰. Поряд з цим вони відзначають і особлива властивість кожної пари кутів, прилеглих до бічної сторони.

З метою підготовки учнів до засвоєння доведення теореми про властивості середньої лінії трапеції корисно перед доведенням теореми розв’язати вправу: «Дана трапеція з основами і . Через точку і сторони проведено пряму, що перетинає пряму в точці . Доведіть, що точка ділить відрізок навпіл ». Після розв’язування цієї вправи до доведення теореми можна залучити учнів.

Нехай дано трапеція з основами і і нехай - середня лінія трапеції (мал.10.).

B C

Q P

A E

D

Мал.10.

Проведемо пряму і нехай вона перетинає пряму в точці .

1. Порівняйте трикутники і .

2. Порівняйте відрізки і ; і .

3. Чим є відрізок в трикутнику ?

4. Що можна сказати про взаємне розташування відрізків і ?

5. Користуючись теоремою про середню лінію трикутника, знайдіть , враховуючи, що .

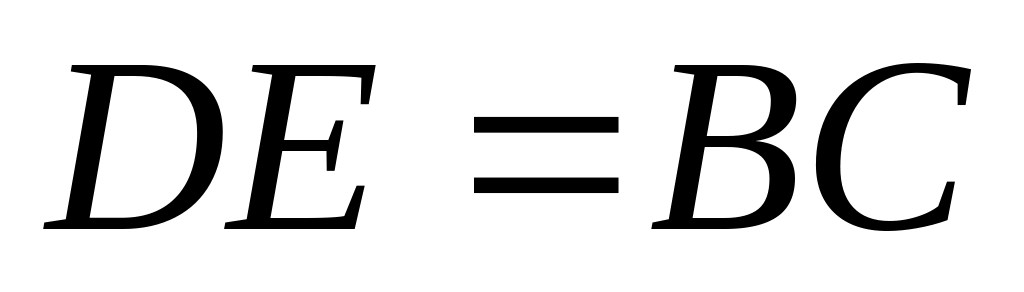6. Які властивості має середня лінія трапеції?