Методичні особливості вивчення теми «Чотирикутники»

У 8 класі

1. Аналіз генезису понять з теми «Чотирикутники» .

Існують різні методичні підходи до введення поняття чотирикутника. Можна спочатку ввести означення багатокутника, а чотирикутник розглянути як окремий вид багатокутника. Такий підхід реалізовано в [5]. У [10] спочатку наводиться означення чотирикутника як фігури, складеної з чотирьох точок і чотирьох відрізків, що послідовно з’єднують їх . У цьому разі жодні три з даних точок не лежать на одній прямій.

Під час пояснення поняття чотирикутника доцільно використати наочні засоби – модель чотирикутника, виготовлену з дроту. На цьому етапі навчання не передбачено вводити поняття плоского й опуклого чотирикутників, тому, розв’язуючи вправи на підведення фігур до названих понять, доцільно використати фігури, які до них належать (мал.1., а, б), і такі, що до них не належать (мал. 2.).

D

B C

а б A

Мал.1. Мал.2.

На уроці, на якому вводитися поняття чотирикутника, учні мають засвоїти елементи чотирикутника (вершини, сторони, сусідні вершини, сусідні сторони, протилежні вершини, протилежні сторони, діагоналі) та відповідну термінологію, навчитись зображувати чотирикутники і позначати їхні вершини. Слід зауважити, що чотирикутник позначають послідовним записом його вершин, наприклад чотирикутник . Учні мають уміти вказувати вершини і сторони намальованого чотирикутника.

Для учнів може виявитись цікавою умова, яка визначає довільний чотирикутник, тобто забезпечує можливість його побудови за допомогою циркуля та лінійки. Дехто з учнів може вважати, що за аналогією з довільним трикутником, який визначається трьома елементами, з яких хоча б один має бути лінійним, чотирикутник визначається чотирма. Потрібно показати, що це не так. Справді, довільний чотирикутник можна розбити діагоналлю на два трикутники. Один з них визначається (може бути побудований) трьома елементами, принаймні один з яких має бути лінійним. Для того щоб було визначено (побудовано) другий трикутник, потрібно задати ще два елементи, оскільки один елемент у трикутників спільний.

У чинних підручниках здійснено різний підхід до введення окремих видів чотирикутників. У [5] спочатку розглянуто паралелограм, потім – прямокутник, ромб, квадрат, і лише наприкінці – трапецію.

У [10] спочатку вивчають паралелограм і трапецію, а потім – прямокутник, ромб, квадрат. Підхід, застосований у [5], на наш погляд, вдаліший, оскільки послідовність вивчення всіх видів паралелограма не порушується вивченням фігури, яка до паралелограма не належить.

У шкільному курсі геометрії із всіх багатокутників більш менш детально вивчаються тільки трикутники і чотирикутники. Під час ознайомлення з рештою видів багатокутників обмежуються тільки питанням про суму внутрішніх і зовнішніх кутів та для правильних многокутників залежності радіусів вписаного і описаного кола від кількості сторін.

У темі «Чотирикутники» значно зростає роль логічного елементу в курсі геометрії. Особливо це виявляється при вивченні класифікації чотирикутників, що тісно пов'язане з складанням означень різних видів чотирикутників, зокрема із означеннями паралелограмів.

Так, наприклад, у означенні паралелограма входить завжди одна і та ж родова ознака — це є чотирикутник, а видові ознаки можуть бути різні: протилежні сторони попарно паралельні, або вони попарно рівні, або діагоналі при своєму перетині діляться навпіл. Та ж особливість є у означеннях прямокутника і ромба, які характеризуються однією і тією ж родовою ознакою (це — паралелограми). А квадрат можна означити за допомогою однієї з двох найближчих родових ознак (це прямокутник або ромб).

Ці ж приклади дозволяють відзначити і такий факт, що у всіх цих означеннях: видова відмінність у означенні однієї фігури береться за родову ознаку у означенні іншої фігури. Наприклад: для паралелограма родова ознака — чотирикутник, видова ознака — протилежні сторони попарно паралельні; прямокутник: родова ознака — паралелограм, видова ознака — прямий кут; квадрат: родова ознака — прямокутник, видова ознака — суміжні сторони рівні.

У зв'язку з цим слід зазначити ще одне явище: квадрат — окремий випадок прямокутника, прямокутник — окремий випадок паралелограма, паралелограм — окремий випадок чотирикутника.

О пуклий чотирикутник

т рапеція

дві і тільки дві протилежні сторони паралельні

м ає одну вісь симетрії що містить одну з діагоналей

дельтоїд

паралелограм

будь-які дві протилежні сторони паралельні

ромб

всі сторони рівні

всі кути рівні

прямокутник

всі кути рівні

всі сторони рівні

квадрат

Схема 1

Варто зауважити, що існує й інший підхід до означення чотирикутників, за якого трапецію означають як опуклий чотирикутник, в якого дві сторони паралельні. В цьому означенні немає жодних зумовлень стосовно двох інших сторін. Згідно з ним паралелограм є окремим видом трапеції. Про переваги такого підходу йдеться в підручнику для педагогічних інститутів М. М. Бескіна «Методика геометрии». [ 3]

Після вивчення означень і властивостей всіх видів чотирикутників доцільно навести учням їх класифікацію у вигляді кругів Ейлера (мал.3.). У цьому разі слід звернути увагу учнів на те, що кожний прямокутник, ромб, квадрат є паралелограмом. А кожний квадрат є одночасно ромбом і прямокутником. Усім чотирикутникам, які належать до множини паралелограмів, притаманні властивості

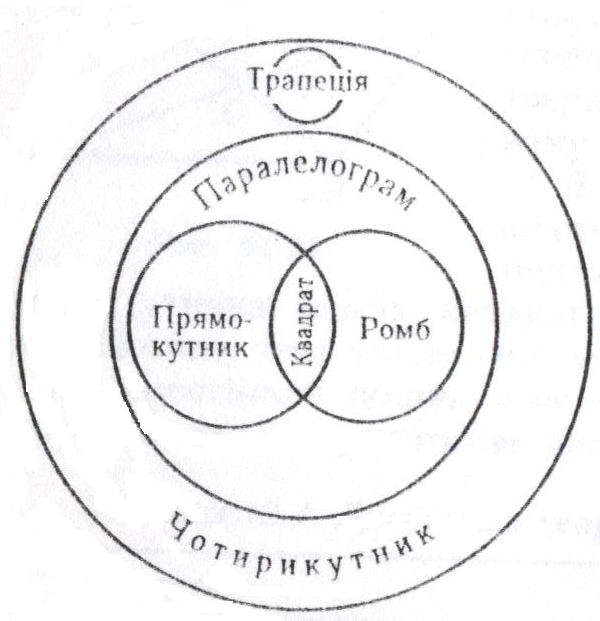
Мал.3.

паралелограма, тобто родового поняття. Водночас певний вид паралелограмів має свої властивості, при чому такі властивості притаманні не кожному паралелограму. Наприклад, у ромба діагоналі взаємно перпендикулярні, а у прямокутника – рівні.

На особливу увагу заслуговує питання щодо засвоєння учнями ознак і властивостей різних видів чотирикутників.

У методиці математики загально прийнято називати ознаками твердження (теореми або задачі на доведення), за допомогою яких можна визначити, що певний об’єкт (наприклад, чотирикутник) належить до певного класу об’єктів (наприклад, прямокутників). Отже, ознака – це прикмета, за якою розпізнають фігури. Водночас в означенні будь-якого поняття зазначено його загальні істотні властивості. З іншого боку, сукупність загальних істотних властивостей понять, заданих в означенні, також становить ознаку поняття. Тому доцільно після введення означення кожного виду чотирикутників робити два висновки щодо його властивостей і ознаки, які випливають безпосередньо з означення. Наприклад, після розгляду означення паралелограма слід звернути увагу учнів на те, що означення дає змогу зробити два висновки: 1) якщо відомо, що деякий чотирикутник є паралелограмом, то можна стверджувати, що його протилежні сторони паралельні (властивість сторін паралелограма); 2) якщо відомо, що в деякому чотирикутнику протилежні сторони попарно паралельні, то він паралелограм (ознака паралелограма).

Властивості окремих видів чотирикутників формулюють у вигляді спеціальних тверджень. Наприклад, у [5] стосовно паралелограма це теореми 6.2, 6.3.

Ознаки окремих видів чотирикутників формулюють також у вигляді теорем і задач на доведення. Тому на завершення вивчення кожного виду чотирикутників потрібно систематизувати всі його ознаки, оскільки, як і властивості, вони мають широко використовуватися надалі для розв’язування задач. Наприклад, до ознак паралелограма крім сформульованої раніше на основі означення належать також твердження:

якщо діагоналі чотирикутника перетинаються і в точці перетину діляться навпіл, то цей чотирикутник – паралелограм;

якщо у чотирикутника дві сторони паралельні й рівні, то він – паралелограм.

Описаний процес складання класифікації чотирикутників, зокрема опуклих чотирикутників, в основу якого покладена послідовна цілеспрямована деформація кожної знову отриманої фігури (отримують спочатку паралельні, а потім і рівні сторони, потім прямі кути), дозволяє однозначно з'ясувати генетичний характер утворення кожного часткового виду опуклих чотирикутників: з чотирикутника з непаралельними сторонами виходять трапеції і паралелограм, з паралелограмів — ромби і прямокутники, з ромбів і прямокутників — квадрати.

З'ясування цього генезису — походження однієї фігури з іншої — допомагає чіткому сприйманню самих геометричних образів, з'ясуванню зв'язків між ними, а це дозволяє поширювати властивості однієї більш загальної фігури (наприклад, паралелограма) на часткові види (на прямокутники, ромби і квадрати).

Особливо великого значення набуває з'ясування генетичних зв'язків при складанні означень часткових видів опуклих чотирикутників: учні вперше мають можливість зрозуміти відносний характер родової і видової ознак того або іншого поняття. Так, наприклад, паралельність обох пар протилежних сторін опуклого чотирикутника є видовою ознакою його, через що цьому чотирикутнику і присвоюється назва паралелограма. А у означенні прямокутника або ромба та ж ознака — паралельність обох пар протилежних сторін — стає родовою ознакою (прямокутник або ромб є паралелограм, тобто чотирикутник з паралельними протилежними сторонами).