Алгебраїчний

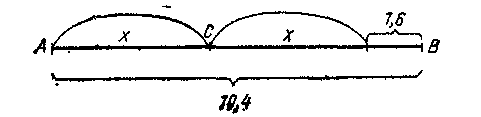
х+х+1,6 = 10,4,

2х + 1,6 = 10,4,

2x = 10,4—1,6,

2х = 8,8,

х = 4,4,

х + l,6 = 6.

Арифметичний

1. Скільки метрів полотна було б в двох частинах, якби їх довжини були однакової довжини меншої частини?

10,4 м - 1,6 м = 8,8 м.

2. Яка довжина меншої частини?

8,8 м : 2=4,4 м.

3. Яка довжина більшої частини?

4,4 м + 1,6 м= 6 м.

Ця задача дає можливість продемонструвати як арифметичний, так і алгебраїчний спосіб, з явною перевагою останнього.

Задача 6. Щоб приготувати суміш для поліровки мідних виробів, беруть 10 частин води, 5 частин нашатирного спирту і 2 частини крейди (по масі). Скільки грамів кожної речовини треба узяти щоб приготувати 340 г суміші?

Для розв’язування такої задачі часто обирають алгебраїчний спосіб. Проте з погляду життєвого досвіду (кулінарні рецепти, різні побутові суміші типу клеї і т.п.) поняття «частина» здається абсолютно природним, маніпулювання частинами в реальному житті відбувається на рівні напівусних обчислень. Розв’язування задач на частини арифметичним способом не викликає труднощів в учнів. Звичайно, не можна наполягати на тому, щоб задачі на частини завжди розв'язувалися арифметично, але показати такий підхід учням потрібно. Це дозволить розширити їх математичний кругозір і збагатити набір математичних прийомів, що використовуються на практиці.

З розглянутих прикладів видно, які широкі можливості має задачний матеріал V-VI класів для розвитку в учнів здатності вибрати оптимальний метод розв’язування поставленої задачі.

Коли в результаті аналізу умови задачі вирішується питання про метод розв’язування, то залишається тільки оформити його.

Оформлення задач, що розв’язуються складанням рівняння, в основному одноманітне, можливі тільки відмінності у поясненнях. Що стосується арифметичного способу, то він вимагає записів або по діях (з поясненнями), або у вигляді числового виразу. Як вже згадувалося, прагнення до економії часу часто приводить до того, що пояснення обмежуються двома-трьома словами, і задачу відрізняє від обчислювальної вправи тільки найменування в результаті.

Як можна зробити змістовнішим етап оформлення розв’язування?

По-перше, необхідно покращити наявні форми роботи — запис розв’язування у вигляді дій з поясненнями або у вигляді числового виразу. Складання числового виразу, природно, викликає більше утруднень. Тому на перших порах доцільно пропонувати учням складати числовий вираз тільки після того, як задача розв’язана по діях. Але у будь-якому випадку обчислювальний аспект не повинен розглядатися як основна мета. Необхідно більше уваги приділяти змістовній насиченості пояснень, оскільки саме вони допомагають учню набувати навик письмового оформлення міркувань.

Форма запитань володіє істотними перевагами, але це не означає, що за допомогою них потрібно вирішувати основну масу задач. Розв’язування запитаннями вимагає значних витрат часу. Проте така форма роботи знову повинна зайняти своє місце в методиці навчання розв’язування задач в V-VI класах. І зараз багато досвідчених вчителів надають велику увагу арифметичному методу і його оформленню у вигляді запитань. Аналіз їх роботи показує, що запитання допомагають учням представити розв’язування задачі як цілісну систему послідовних, логічно взаємозв'язаних кроків (що особливо важливе для подальшого вивчення систематичних курсів). Необхідність проводити обгрунтовані міркування розвиває у дітей здатність чітко і лаконічно висловлювати свої думки, аргументувати свої дії, розковує їх, поступово знімаючи проблему «математичної недалекоглядності».

Останній етап розв’язування — інтерпретація отриманого результату. Звичайно робота на цьому етапі зводиться до запису відповіді. У кращому разі проводиться перевірка одержаного числового результату підстановкою його в умову задачі.

Таким чином, замість підбиття підсумку всієї виконаної роботи часто проводиться остаточне формальне оформлення розв’язування. Адже тільки завершивши розв’язування, учень може сприйняти задачу як цілісну структуру, зробити деякі загальні висновки, що виходять за рамки зроблених дій. З'являється можливість розглянути числове значення шуканої величини на іншому якісному рівні, осмислити його у взаємозв'язках з іншими компонентами задачі, оцінити повноту і реальність як з погляду проведеного розв’язування, так і погодившися із здоровим глуздом. Доцільно іноді пропонувати учням задачі, в яких при зовнішній стандартності фабули виходить нереальна відповідь. Наприклад, в задачі на рух можна так підібрати числові параметри, щоб знайдена швидкість велосипедиста перевищить швидкість електропоїзда. Такі задачі викликають у дітей настороженість по відношенню до одержаного результату, аргументує доцільність аналізу знайденого числового параметра.

В деяких випадках можна розглянути можливі зміни результату залежно від змін основних параметрів задачі. Наприклад, в задачі вимагалося знайти час, за який було пройдено деякий шлях при вказаній постійній швидкості. Поставимо запитання: «Як зміниться одержаний результат при збільшенні (зменшенні) швидкості або відстані?» Відповідь на нього допоможе розкрити динаміку процесу, побачити закон зміни однієї величини при зміні іншої.

Систематична робота з аналізу отриманого розв’язання дозволить прищепити учням первинні навики узагальнення, підведе їх до сприйняття окремого випадку як прояву загальної закономірності.

Таким чином, реалізація розвиваючого потенціалу текстової задачі можлива на кожному етапі її розв’язування.