Федеральное государственное автономное

образовательное учреждение

высшего профессионального образования

«СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»

Инженерно-строительный институт

Кафедра «Автомобильные дороги и городские сооружения»

Отчет по лабораторной работе № 1 решение системы линейных алгебраических уравнений (слау) Вариант № 25

Преподаватель __________ ______________

подпись, дата инициалы, фамилия

Студент ____________ ________________ __________ _____________

номер группы номер зачетной книжки подпись, дата инициалы, фамилия

Красноярск 2014

Содержание

Содержание ……………………………..………….………………….………..2

1. Цель и задачи лабораторной работы……….……………………. ……..3

2. Исходные данные……………………..……………………………….……3

3. Решение СЛАУ матричным методом………………………………….. …3

4. Решение СЛАУ с помощью определителей (методом Крамера)……. …..4

5. Решение СЛАУ методом Гаусса…………………………………..… .…….6

Вывод……………………………………………………………………….….…6

Список использованных источников………………………………………..…6

gavtan@mail.ru

1 Цель и задачи лабораторной работы

Цель: Освоить несколько вычислительных методов решения системы линейных алгебраических уравнений.

Задачи:

- научиться решать СЛАУ методами Гаусса, Крамера и обратной матрицы;

- реализовать алгоритмы решения с помощью программы Excel;

- получить навыки отладки программы;

- оценить эффективность и область применения данных методов.

2 Исходные данные

Требуется решить систему линейных уравнений

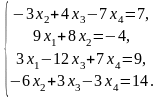(1)

Запишем систему (1) в матричном виде

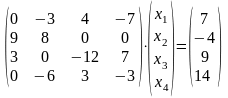. (2)

3 Решение матричным методом

Ход решения:

	А					Х				В
0	-3	4	-7			х1				7
9	8	0	0			х2				-4
3	0	-12	7			х3				9
0	-6	3	-3			х4				14
1. Находим определитель
det A=	-2835
2 Обратная матрица
-0,04233	0,102646	0,025397	0,158025
0,047619	0,009524	-0,02857	-0,17778
-0,15873	0,034921	-0,10476	0,125926
-0,25397	0,015873	-0,04762	0,148148
3 умножаем слева столбец В:
		Х
		1,734039
		-2,45079
		-0,43069
		-0,19577
4 Проверка Умножаем матрицу А на вектор Х
		7
		-4
		9
		14