Аксіома про паралельні прямі і V постулат Евкліда

Ф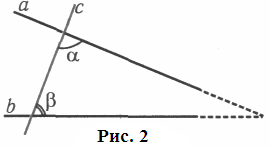 ормулювався V постулат Евкліда так: Якщо при перетині двох прямих а і b прямою с (рис. 2) сума утворених при цьому внутрішніх односторонніх кутів і менша двох прямих кутів (тобто менша 180°; Евклід не застосовував градусної міри кутів), то при достатньому продовженні прямі а і b перетнуться.

Неважко показати, що V постулат Евкліда справді еквівалентний сучасній аксіомі про паралельні прямі. Еквівалентність двох тверджень означає, що з посиланням на одне з них можна вивести інше і навпаки.

Н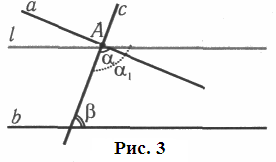 ехай прийнято сучасну аксіому про паралельні прямі. Покажемо, що з неї випливає V постулат Евкліда. Отже, нехай при перетині яких-небудь двох прямих а і b довільною третьою прямою с сума утворених при цьому внутрішніх односторонніх кутів і менша 180° (рис. 3); потрібно довести, що при цій умові прямі а і b перетинаються.

Згідно з аксіомою про паралельні прямі, через точку проходить єдина пряма l, паралельна b. А за відомою властивістю паралельних (яка, в свою чергу, виводиться з аксіоми про паралельні прямі), сума внутрішніх односторонніх кутів і , утворених при перетині паралельних l, b січною с, дорівнює 180°. Сума ж . Тому пряма а не збігається з l. А оскільки l — єдина пряма, що проходить через А і не перетинає b, то пряма а уже перетинає b. Що й треба було довести.

Навпаки, для виведення аксіоми про паралельні прямі з V постулату Евкліда попередньо доводять таку властивість зовнішнього кута трикутника: зовнішній кут трикутника більший від будь-якого внутрішнього, не суміжного з ним. Ця теорема, звичайно, елементарно випливає зі «шкільної» теореми про те, що зовнішній кут трикутника дорівнює сумі двох внутрішніх, не суміжних з ним. Але ця «шкільна» теорема доводиться з посиланням на властивість паралельних прямих, які, в свою чергу, випливають з аксіоми про паралельні прямі. Тому посилатися на неї не можна. Інакше здійснимо хибне логічне коло: доводили б аксіому про паралельні прямі ... на основі аксіоми про паралельні прямі. Тому потрібно провести таке доведення, яке не залежить від цієї аксіоми.

О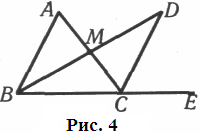 тже, нехай маємо ∆АВС (рис. 4). Доведемо для прикладу, що зовнішній кут АСЕ при вершині С більший від внутрішнього кута А. Нехай М — середина сторони АС. Проведемо промінь ВМ і, відклавши на ньому відрізок МD=ВМ, з'єднаємо відрізком точки D і С. Одержаться рівні трикутники АМD і СМD (переконайтеся в цьому), звідки . Але  — це лише частина кута АСЕ. Тому , що й треба було довести.

Т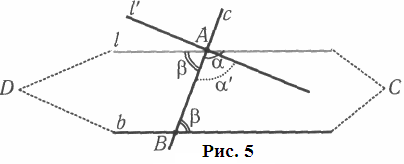 епер повернемося до проблеми еквівалентності аксіоми про паралельні прямі і V постулату Евкліда. Припустимо, що має місце V постулат Евкліда, і доведемо, що тоді матиме місце і аксіома про паралельні прямі.

Нехай у площині маємо пряму b і точку А поза нею (рис. 5). Проведемо через А довільну січну с, а потім — пряму l, яка з того боку від січної с, з якого лежить кут , утворює з с кут . Тоді з іншого боку утвориться кут . Пряма l не може перетнутися з b, бо якби таке трапилося, то утворився б трикутник АВС (або АBD), у якому внутрішній кут при вершині В дорівнював би зовнішньому куту при вершині А. А це суперечило б теоремі про зовнішній кут трикутника. Тому l║b. Таким чином, існування прямої, що проходить через точку А і паралельна прямій b, доведено (причому, зауважимо, навіть без посилання на V постулат Евкліда). Залишається довести її єдиність (а для цього уже V постулат буде задіяно).

Припустимо, що через точку А проходить ще одна пряма , паралельна b. Якщо пряма пройде частково всередині кута , то пряма с утворюватиме з прямими i b внутрішні односторонні кути і , сума яких менша 180° (оскільки ). Тоді, за V постулатом Евкліда прямі і b перетнуться, що суперечить припущенню. Якщо ж пряма пройде частково всередині кута , то аналогічний висновок одержимо по інший бік від січної с. Тому зроблене припущення неправильне. Отже, пряма l — єдина. Доведення еквівалентності завершено.