Фалес та ідея логічного обґрунтування у геометрії

Давні греки найбільше пошановували сімох мудреців: Солона з Афін, Піттака з Мітілени (на о. Лесбос), Періандра з Коринфа, Біанта з Прієни, Клеобула з Лінди (на о. Родос), Хілона зі Спарти і Фалеса з Мілета. Шестеро з них були правителями і законодавцями. Проте першість одностайно віддавали ученому-філософу Фалесу. «За що ж ми того Фалеса славимо?» — ставиться риторичне запитання в комедії «Хмари» грецького драматурга Арістофана.

Жив Фалес наприкінці VII — в першій половині VI ст. до н.е. В молоді роки, ймовірно, був купцем і здійснив декілька подорожей у Єгипет і Вавилон. Там він почерпнув чимало знань зі скарбниці східної мудрості, а повернувшись на батьківщину, організував філософську школу. Найяскравіше Фалесова мудрість виявилась у передбаченні повного сонячного затемнення, яке сталося 28 травня 585 р. до н.е. Саме в цей день відбувалася битва мідян з лідійцями при Галісі. Геродот розповідає, що коли день перетворився в ніч, то обидва війська так налякалися, що негайно уклали мир. Найімовірніше, що своє передбачення Фалес здійснив на основі запозичених у жерців даних астрономічних спостережень. Ще перебуваючи в Єгипті, Фалес здивував тамтешнього фараона Амазіса, зумівши визначити висоту найбільших пірамід за величиною їхньої тіні. Для цього він виміряв довжину тіні від піраміди в той час, коли довжина тіні від вертикально поставленого кілка дорівнювала його висоті.

Плутарх стверджує, що Фалесу навіть не конче було чекати цього моменту. Він нібито міг скористатися і більш «теоретичним» способом, встановивши відношення між довжиною допоміжного кілка і його тінню. Йдеться, очевидно, про використання властивості пропорційності сторін подібних трикутників.

Фалес — перший учений, з ім'ям якого пов'язують доведення конкретних геометричних фактів. Неоплатонік Прокл Діодох (V ст. н.е.) у своїх коментарях до «Начал» Евкліда, посилаючись на втрачену «Історію геометрії та астрономії» учня Арістотеля Евдема Родоського (IV ст. до н.е.), повідомляє про Фалеса таке:

«Він першим довів, що діаметр ділить круг навпіл».

«Крім багатьох інших тверджень, йому належить також твердження про рівність кутів при основі рівнобедреного трикутника; за давнім звичаєм, він називав ці кути не рівними, а подібними».

«Згідно з Евдемом, він відкрив, що при перетині двох паралельних прямих утворюються рівні кути, але не подав доведення цього твердження».

«Теорему про рівність двох трикутників, у яких рівні сторона і два кути, Евдем приписує Фалесу, зазначаючи, що для доведення його способу визначення відстаней до кораблів на морі необхідно використовувати саме цю теорему про рівність».

Як бачимо, останнє твердження приписується Фалесу на тій основі, що воно є ключовим у запропонованому ним способі знаходження відстаней до недосяжних об'єктів (таких, як корабель на морі). Однак, яким саме був цей метод, досі достеменно невідомо. Відомі дві можливі реконструкції Фалесового методу — «горизонтальна» і «вертикальна».

С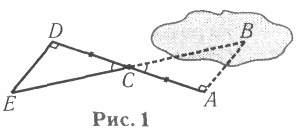 уть першої полягає в наступному. Для знаходження відстані від доступної точки А до недосяжної точки В будують перпендикуляр АD до прямої АВ довільної довжини (рис. 1). Потім ділять його точкою С навпіл, а в точці D проводять перпендикуляр DЕ до прямої АD у протилежному до АВ напрямку. Точка Е вибирається таким чином, щоб точки В, С і Е лежали на одній прямій. Тоді довжина відрізка DЕ — шукана відстань.

Довести це дуже просто, спираючись на наведені Евдемом твердження. Крім того, на користь такої реконструкції свідчить те, що аналогічний спосіб вимірювання використовував і римський землемір Марк Юній Ніпс — свідчення про це дійшли до наших днів.

«Вертикальний» спосіб вимірювання міг полягати у визначенні кута зору АЕВ на недосяжний предмет В з позиції спостерігача, розташованого на підвищенні (на скелі чи на башті) (рис. 2), і в наступній пеленгації під цим кутом певного об'єкта С на суші, відстань до якого відома.

Н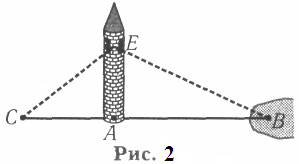 а користь цієї реконструкції свідчать археологічні знахідки циркулів з виском, що уможливлювали фіксацію кута зору саме до вертикалі. Як тут не згадати, що Писфетер у «Птахах» Арістофана захоплено вигукує до Метона, коли той, озброївшись циркулем і лінійкою, швидко виконує складні розрахунки: «Істинно, ти — Фалес!».

Друга реконструкція добре узгоджується з тією думкою, що свої теореми Фалес, мабуть, доводив методом суміщення поворотом (перегином). Адже з геометричної точки зору другий спосіб полягає у суміщенні трикутників АВЕ і АСЕ способом повороту першого з них навколо сторони АЕ.

Крім наведених вище чотирьох геометричних тверджень, деякі автори приписують Фалесу доведення теореми про те, що вписаний у коло кут, який спирається на діаметр, є прямим. Кажуть навіть, що за це відкриття вдячний Фалес приніс у жертву богам бика. Щоправда, одностайності у цьому питанні немає: наприклад, Аполлодор приписує доведення названої теореми Піфагору.

На перший погляд, математичні відкриття Фалеса можуть здатися сучасному читачеві не вартими тієї уваги, яка їм надається в історико-математичній літературі. Але не за геометричні твердження, які, без сумніву, були відомі і до Фалеса, а за сам факт їх логічного доведення Фалеса називають першим серед математиків. Саме з Фалесом пов'язаний початок нової епохи у розвитку науки. «Ми майже нічого не знаємо про історію цієї революції в способі мислення, — писав Іммануїл Кант. — Але легенда, передана нам Діогеном Лаертським, який повідомляє ім'я уявного винахідника дріб'язкових, за загальною думкою — навіть таких, що не потребують доведення, елементарних геометричних тверджень, показує, що згадка про зміни, викликані першими ознаками відкриття цього нового шляху, видавалась надзвичайно важливою в очах математиків і тому залишила незгладний слід у їхній свідомості».

Архімед

З усіх великих античних учених, які займалися математичними дослідженнями, Архімед залишився чи не найпривабливішим для нащадків. Вирішальним чином цьому посприяла винятково плідна його діяльність не тільки як дослідника-теоретика, але і як інженера-практика. Відомо, що Архімед керував усією інженерною службою у сіракузького царя Гієрона, в тому числі — і під час історичної оборони Сіракуз від римлян під час 2-ї Пунічної війни (Сіракузи — рідне місто Архімеда на о. Сицилія). І хоча Плутарх стверджує, що своїм механічним винаходам Архімед не надавав особливого значення, розглядаючи їх лише як «забави геометрії», проте і сучасників, і нащадків вражали в першу чергу ці його «забави».

Плутарх розповідає, що воїни римського консула Марцелла були надовго затримані біля стін Сіракуз небаченими досі машинами. В бійницях були виставлені катапульти, які скидали град ядер і каміння, берегові крани, повертаючись, зачіплювали кораблі за щогли, підіймали і скидали їх у воду, а великі ввігнуті дзеркала палили ворога вогнем. Усе це наводило на нападників невимовний жах. «Як тільки вони помічали, — пише Плутарх, — що із-за фортечного муру показується якийсь канат або колода, то з криком починали тікати, жахаючись, що ось Архімед знову придумав якусь нову машину їм на погибель».

В іншій історії повідомляється, що Архімед збудував таку систему блоків і важелів, що з допомогою неї одна людина могла спустити на воду новозбудований величезний корабель «Сіракосія», який призначався для перевезення зерна. Крилатою стала фраза, вимовлена нібито при цьому Архімедом: «Дайте мені точку опори — і я переверну Землю». Для відкачування води в разі необхідності на «Сіракосії» було встановлено ще один видатний винахід Архімеда — так званий архімедів гвинт.

Надзвичайно популярною є й історія про золоту царську корону, чистоту золота в якій Архімед перевірив на основі відкритого ним закону про виштовхувальну силу.

Архімед загинув на 75-му році життя від руки римського воїна. Сивий старець сидів, розглядаючи накреслені перед собою на піску фігури. «Не чіпай моїх креслень», — були його останні слова.

Власне математичними дослідженнями Архімед почав займатися уже в зрілому віці — після 40 років. Але це не завадило йому перевершити усіх математиків, які жили як до нього, так і впродовж багатьох наступних століть — аж до Ньютона і Лейбніца в XVII ст.

Основний напрям математичних досліджень Архімеда — вимірювання довжин, площ та об'ємів геометричних фігур. Створені ним для цього методи по суті були методами диференціального та інтегрального числення, відкритими аж через 2 тисячі років після Архімеда.

Визначним відкриттям Архімеда стали і його напівправильні многогранники, названі пізніше Архімедовими тілами.